_浙江省宁波市鄞州区七校联考2022-2023学年七年级上学期期中数学试卷(含答案)

这是一份_浙江省宁波市鄞州区七校联考2022-2023学年七年级上学期期中数学试卷(含答案)，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年浙江省宁波市鄞州区七校联考七年级第一学期期中数学试卷
一、单选题（每小题3分，共30分）
1．﹣2022的相反数是（　　）
A．﹣ B． C．﹣2022 D．2022
2．我国的陆地面积为9600000平方千米，9600000用科学记数法可表示为（　　）
A．96×105 B．9.6×106 C．0.96×107 D．960×104
3．如果x是有理数，那么下列各式中一定比0大的是（　　）
A．2021﹣x B．2021+x C．|x|+2021 D．|x|
4．在实数：π，，，，0.1010010001⋯（每2个1之间依次多一个0）中，无理数的个数是（　　）
A．1个 B．2个 C．3个 D．4个
5．实数在哪两个相邻的整数之间（　　）
A．0和1之间 B．1和2之间 C．2和3之间 D．3和4之间
6．如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则E点所表示的数为（　　）

A． B． C． D．
7．已知|x|＝6，y2＝4，且xy＜0．则x+y的值为（　　）
A．4 B．﹣4 C．4或﹣4 D．2或﹣2
8．已知：21＝2，22＝4，23＝8，24＝16，25＝32，…，那么22021的个位数字是（　　）
A．2 B．4 C．6 D．8
9．若abc≠0，则++的值为（　　）
A．±3或±1 B．±3或0或±1 C．±3或0 D．0或±1
10．如果一个正数x的平方根是2a﹣3和5﹣a，那么x的值是（　　）
A．﹣2 B．7 C．﹣7 D．49
二、填空题（每小题3分，共18分）
11．﹣的倒数等于　 　．
12．已知a+3b﹣4＝0，则9b+3a﹣11的值是 　 　．
13．已知a是的整数部分，b是它的小数部分，则2a+b﹣＝　 　．
14．若“！”是一种数学运算符号，并且：1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…，则＝　 　．
15．数轴上表示1，的对应点分别为点A，点B．若点B关于点A的对称点为点C，则点C所表示的数为　 　．

16．如图，将直径为1个单位长度的圆沿着数轴向右滚动一周，圆上一点由表示﹣2的点A到达点A'，则点A'对应的数是　 　．

17．计算：
（1）﹣2+（﹣7）﹣3+8；
（2）﹣12021+（）×|﹣6|÷22；
（3）；
（4）．
三、解答题（18题4分，19，20，21，22题各6分，23，24各8分）
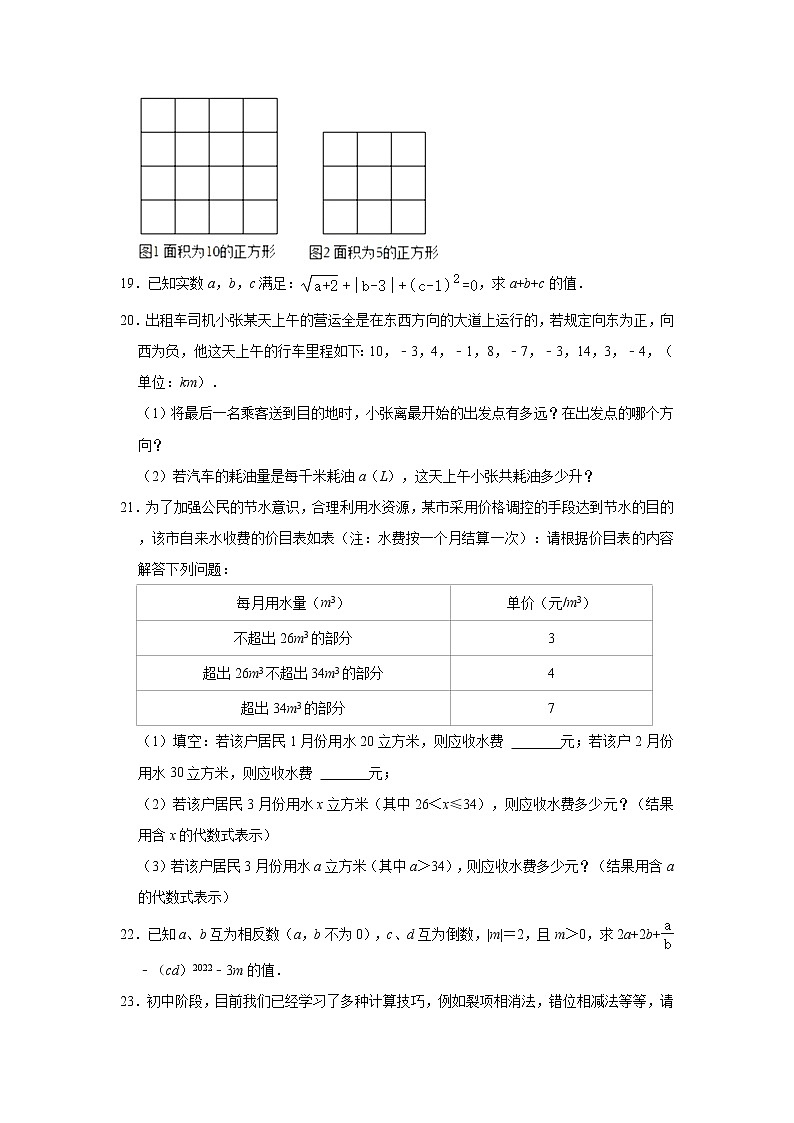
18．在如图所示的方格中，按要求画出相应面积的正方形，要求正方形的每个顶点在方格图的格点．

19．已知实数a，b，c满足：，求a+b+c的值．
20．出租车司机小张某天上午的营运全是在东西方向的大道上运行的，若规定向东为正，向西为负，他这天上午的行车里程如下：10，﹣3，4，﹣1，8，﹣7，﹣3，14，3，﹣4，（单位：km）．
（1）将最后一名乘客送到目的地时，小张离最开始的出发点有多远？在出发点的哪个方向？
（2）若汽车的耗油量是每千米耗油a（L），这天上午小张共耗油多少升？
21．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如表（注：水费按一个月结算一次）：请根据价目表的内容解答下列问题：
每月用水量（m3）
单价（元/m3）
不超出26m3的部分
3
超出26m3不超出34m3的部分
4
超出34m3的部分
7
（1）填空：若该户居民1月份用水20立方米，则应收水费 　 　元；若该户2月份用水30立方米，则应收水费 　 　元；
（2）若该户居民3月份用水x立方米（其中26＜x≤34），则应收水费多少元？（结果用含x的代数式表示）
（3）若该户居民3月份用水a立方米（其中a＞34），则应收水费多少元？（结果用含a的代数式表示）
22．已知a、b互为相反数（a，b不为0），c、d互为倒数，|m|＝2，且m＞0，求2a+2b+﹣（cd）2022﹣3m的值．
23．初中阶段，目前我们已经学习了多种计算技巧，例如裂项相消法，错位相减法等等，请计算下列各式：
（1）＝　 　；
（2）＝　 　；
（3）＝　 　．
24．“数形结合”是重要的数学思想．如：|3﹣（﹣2）|表示3与﹣2差的绝对值，实际上也可以理解为3与﹣2在数轴上所对应的两个点之间的距离．进一步地，数轴上两个点A，B所对应的数分别用a，b表示，那么A，B两点之间的距离表示为AB＝|a﹣b|．利用此结论，回答以下问题：

（1）数轴上﹣2和5这两点之间的距离为 　 　．
（2）若x表示一个实数，|x+2|+|x﹣4|的最小值为 　 　．
（3）直接写出所有符合条件的x，使得|x﹣2|+|x+5|＝9，则x的值为 　 　．


参考答案
一、单选题（每小题3分，共30分）
1．﹣2022的相反数是（　　）
A．﹣ B． C．﹣2022 D．2022
【分析】根据相反数的定义直接求解．
解：﹣2022的相反数是2022，
故选：D．
【点评】本题主要考查相反数的定义，熟练掌握相反数的定义是解答此题的关键．
2．我国的陆地面积为9600000平方千米，9600000用科学记数法可表示为（　　）
A．96×105 B．9.6×106 C．0.96×107 D．960×104
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
解：将9600000用科学记数法表示为：9.6×106．
故选：B．
【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．如果x是有理数，那么下列各式中一定比0大的是（　　）
A．2021﹣x B．2021+x C．|x|+2021 D．|x|
【分析】根据有理数的大小比较法则以及绝对值的性质判断即可．
解：A．当x≤2021时，2021﹣x≤0，故本选项不合题意；
B．当x≤﹣2021时，2021+x≤0，故本选项不合题意；
C．∵|x|≥0，
∴|x|+2021≥2021＞0，故本选项符合题意；
D．当x＝0时，|x|＝0，故本选项不合题意；
故选：C．
【点评】此题主要考查了绝对值以及有理数大小比较的方法，熟知有理数比较大小的法则是解题的关键．
4．在实数：π，，，，0.1010010001⋯（每2个1之间依次多一个0）中，无理数的个数是（　　）
A．1个 B．2个 C．3个 D．4个
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解：是分数，属于有理数；
＝3，是整数，属于有理数；
无理数有π，，0.1010010001⋯（每2个1之间依次多一个0），共3个．
故选：C．
【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
5．实数在哪两个相邻的整数之间（　　）
A．0和1之间 B．1和2之间 C．2和3之间 D．3和4之间
【分析】根据算术平方根的定义，估算无理数的大小即可．
解：∵4＜5＜9，
∴，
即2＜＜3，
故选：C．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．
6．如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则E点所表示的数为（　　）

A． B． C． D．
【分析】根据正方形的边长是面积的算术平方根得AD＝AE＝，结合A点所表示的数及AE间距离可得点E所表示的数．
解：∵正方形ABCD的面积为5，且AD＝AE，
∴AD＝AE＝，
∵点A表示的数是1，且点E在点A右侧，
∴点E表示的数为1+．
故选：B．
【点评】本题主要考查实数与数轴及两点间距离，根据两点间距离及点的位置判断出点所表示的数是关键．
7．已知|x|＝6，y2＝4，且xy＜0．则x+y的值为（　　）
A．4 B．﹣4 C．4或﹣4 D．2或﹣2
【分析】根据题意求出符合条件的x、y的值，再代入要求的式子计算即可．
解：∵|x|＝6，y2＝4，
∴x＝±6，y＝±2，
又∵xy＜0，
∴x＝6，y＝﹣2或x＝﹣6，y＝2，
当x＝6，y＝﹣2时，x+y＝4，
当x＝﹣6，y＝2时，x+y＝﹣4，
故选：C．
【点评】本题考查绝对值的意义，有理数乘法和加法的计算方法，求出相应的x、y的值是正确计算的关键．
8．已知：21＝2，22＝4，23＝8，24＝16，25＝32，…，那么22021的个位数字是（　　）
A．2 B．4 C．6 D．8
【分析】观察21、22、23、24、25、…的个位数字分别为2、4、8、6、2、4、8、6、…，发现每四个为一个周期，所以指数÷4的余数是1，则个位数字为2；余数是2，则个位数字是4；余数是3，则个位数字是8；余数是0，则个位数字是6．
解：2021÷4＝505……1，
∴22021的个位数字是2．
故选：A．
【点评】本题考查尾数特征，观察个位数字特征是解题的关键．
9．若abc≠0，则++的值为（　　）
A．±3或±1 B．±3或0或±1 C．±3或0 D．0或±1
【分析】分4种情况分别计算，根据绝对值的性质化简即可得出答案．
解：若a，b，c都是正数，那么原式＝1+1+1＝3；
若a，b，c中有1个负数，不妨设a是负数，那么原式＝﹣1+1+1＝1；
若a，b，c中有2个负数，不妨设a，b是负数，那么原式＝﹣1+（﹣1）+1＝﹣1；
若a，b，c都是负数，那么原式＝﹣1+（﹣1）+（﹣1）＝﹣3；
故选：A．
【点评】本题考查了绝对值的性质，体现了分类讨论的数学思想，掌握正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值是0是解题的关键．
10．如果一个正数x的平方根是2a﹣3和5﹣a，那么x的值是（　　）
A．﹣2 B．7 C．﹣7 D．49
【分析】依据平方根的性质列出关于a的方程可求得a的值，然后依据平方根的定义求解即可．
解：∵一个正数的x的平方根是2a﹣3与5﹣a，
∴2a﹣3+5﹣a＝0，
解得a＝﹣2．
∴5﹣a＝7．
∴x＝72＝49．
故选：D．
【点评】本题主要考查的是平方根的性质，求得a的值是解题的关键．
二、填空题（每小题3分，共18分）
11．﹣的倒数等于　﹣　．
【分析】先把待分数化为假分数，然后根据倒数的定义求解．
解：﹣1＝﹣，
﹣的倒数为﹣．
故答案为﹣．
【点评】本题考查了倒数的定义：a（a≠0）的倒数为．
12．已知a+3b﹣4＝0，则9b+3a﹣11的值是 　1　．
【分析】由a+3b﹣4＝0，得a+3b＝4，将9b+3a﹣11变形成3（a+3b）﹣11，再整体代入即可得答案．
解：∵a+3b﹣4＝0，
∴a+3b＝4，
∴9b+3a﹣11＝3（a+3b）﹣11＝3×4﹣11＝12﹣11＝1，
故答案为：1．
【点评】本题考查代数式求值，解题的关键是将所求式子变形，再整体代入．
13．已知a是的整数部分，b是它的小数部分，则2a+b﹣＝　3　．
【分析】由于3＜a＜4，则a＝3，b＝﹣3，然后代入所求代数式进行计算即可．
解：∵3＜＜4，
∴a＝3，b＝﹣3，
∴2a+b﹣＝6+＝3，
故答案为：3．
【点评】本题考查了估算无理数的大小，解题的关键是利用完全平方数和算术平方根对无理数的大小进行估算．
14．若“！”是一种数学运算符号，并且：1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…，则＝　9900　．
【分析】100！＝100×99×98×97×…×1，98！＝98×97×…×1．
解：∵100！＝100×99×98×97×…×1，98！＝98×97×…×1．
∴＝＝100×99＝9900．
【点评】此题是定义新运算题型．直接把对应的数字代入所给的式子可求出所要的结果．解题关键是对号入座不要找错对应关系．
15．数轴上表示1，的对应点分别为点A，点B．若点B关于点A的对称点为点C，则点C所表示的数为　2﹣　．

【分析】根据数轴上两点之间线段的长度可得出AB的长度，再由对称即可得出点C所表示的数．
解：∵数轴上表示1，的对应点分别为点A，点B．
∴AB＝﹣1，
∵点B关于点A的对称点为点C，
∴BC＝﹣1，
∴点C所表示的数为2﹣．
故答案为2﹣．
【点评】本题考查了实数与数轴，数轴上的点与实数是一一对应的关系．
16．如图，将直径为1个单位长度的圆沿着数轴向右滚动一周，圆上一点由表示﹣2的点A到达点A'，则点A'对应的数是　﹣2+π　．

【分析】直径为1个单位长度的圆沿着数轴向右滚动一周，圆上一点A运动到了A'的位置，说明AA'之间的距离为圆的周长，再根据数轴的基础知识即可求解出A'所表示的数．
解：
由题AA'之间的距离为直径为1个单位长度的圆的周长
∴AA'＝πd＝π
∵A所表示的数为﹣2
∴A'所表示的数为π﹣2
答：点A'对应的数是π﹣2．
【点评】本题考查数轴和圆的基础知识，圆在数轴上滚动一周的过程中，圆上一点A运动到了A'的位置相当于AA'之间的距离为圆的周长这一点是解题关键．
17．计算：
（1）﹣2+（﹣7）﹣3+8；
（2）﹣12021+（）×|﹣6|÷22；
（3）；
（4）．
【分析】（1）先将减法运算变成加法，再计算求解；
（2）先计算乘方、绝对值和括号里面的，再计算加法；
（3）先运用乘法分配律，再计算加减运算；
（4）先计算乘方、立方根和平方根，再计算除法，最后计算加减．
解：（1）﹣2+（﹣7）﹣3+8
＝﹣2﹣7﹣3+8
＝﹣4；
（2）﹣12021+（）×|﹣6|÷22
＝﹣1+×6×
＝﹣1+
＝﹣；
（3）
＝﹣×12+×12+×12
＝﹣3+8+10
＝15；
（4）
＝﹣8﹣3﹣4×
＝﹣11﹣9
＝﹣20．
【点评】此题考查了实数混合运算的能力，关键是能准确确定运算顺序和方法．
三、解答题（18题4分，19，20，21，22题各6分，23，24各8分）
18．在如图所示的方格中，按要求画出相应面积的正方形，要求正方形的每个顶点在方格图的格点．

【分析】利用勾股定理数形结合的思想画出图形即可．
解：图形如图所示：


【点评】本题考查作图﹣应用与设计作图，正方形的判定和性质等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
19．已知实数a，b，c满足：，求a+b+c的值．
【分析】根据非负数的性质，可求出a、b、c的值，然后将代数式化简，再代值计算．
解：根据题意得：，
解得：．
则（a+b+c）2＝（﹣2+3+1）2＝22＝4．
【点评】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
20．出租车司机小张某天上午的营运全是在东西方向的大道上运行的，若规定向东为正，向西为负，他这天上午的行车里程如下：10，﹣3，4，﹣1，8，﹣7，﹣3，14，3，﹣4，（单位：km）．
（1）将最后一名乘客送到目的地时，小张离最开始的出发点有多远？在出发点的哪个方向？
（2）若汽车的耗油量是每千米耗油a（L），这天上午小张共耗油多少升？
【分析】（1）把所有行车里程相加，然后根据正负数的意义解答；
（2）先求出行车里程的绝对值的和，再乘以a计算即可得解．
解：（1）10﹣3+4﹣1+8﹣7﹣3+14+3﹣4
＝39﹣18
＝21（千米）．
故将最后一名乘客送到目的地时，小张离最开始的出发点21千米，在出发点的东边；
（2）10+3+4+1+8+7+3+14+3+4＝57（千米），
57×a＝57a（升）．
答：这天上午小张共耗油57a升．
【点评】此题主要考查了列代数式，正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
21．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如表（注：水费按一个月结算一次）：请根据价目表的内容解答下列问题：
每月用水量（m3）
单价（元/m3）
不超出26m3的部分
3
超出26m3不超出34m3的部分
4
超出34m3的部分
7
（1）填空：若该户居民1月份用水20立方米，则应收水费 　60　元；若该户2月份用水30立方米，则应收水费 　94　元；
（2）若该户居民3月份用水x立方米（其中26＜x≤34），则应收水费多少元？（结果用含x的代数式表示）
（3）若该户居民3月份用水a立方米（其中a＞34），则应收水费多少元？（结果用含a的代数式表示）
【分析】（1）利用总价＝单价×数量，结合价目表的内容，即可求出结论；
（2）利用应收水费＝3×26+4×（x﹣26），即可用含x的代数式表示出应收水费；
（3）利用应收水费＝3×26+4×（34﹣26）+7×超过34立方米的数量，即可用含a的代数式表示出应收水费．
解：（1）3×20＝60（元），
3×26+4×（30﹣26）
＝3×26+4×4
＝78+16
＝94（元）．
故答案为：60；94．
（2）依题意得：应收水费为3×26+4×（x﹣26）＝（4x﹣26）元．
故应收水费（4x﹣26）元；
（3）依题意得：应收水费为3×26+4×（34﹣26）+7（a﹣34）＝（7a﹣128）元．
故应收水费（7a﹣128）元．
【点评】本题考查了有理数的混合运算以及列代数式，解题的关键是：（1）根据各数量之间的关系，列式计算；（2）根据各数量之间的关系，用含x的代数式表示出应收水费；（3）根据各数量之间的关系，用含a的代数式表示出应收水费．
22．已知a、b互为相反数（a，b不为0），c、d互为倒数，|m|＝2，且m＞0，求2a+2b+﹣（cd）2022﹣3m的值．
【分析】由题意可得a+b＝0，cd＝1，m＝2，再把相应的值代入进行运算即可．
解：∵a、b互为相反数（a，b不为0），c、d互为倒数，|m|＝2，且m＞0，
∴a+b＝0，cd＝1，m＝2，，
∴2a+2b+﹣（cd）2022﹣3m
＝2（a+b）+﹣（cd）2022﹣3m
＝2×0+（﹣1）﹣12022﹣3×2
＝0﹣1﹣1﹣6
＝﹣8．
【点评】本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．
23．初中阶段，目前我们已经学习了多种计算技巧，例如裂项相消法，错位相减法等等，请计算下列各式：
（1）＝　　；
（2）＝　　；
（3）＝　﹣1　．
【分析】（1）裂项后乘以2，将各项相加，消掉和互为相反数的项；
（2）裂项后乘以3，将各项相加，消掉和互为相反数的项；
（3）根据绝对值的性质去掉绝对值，即可消掉．
解：（1）原式＝2×（1﹣+﹣+﹣+•••+﹣）
＝2×（1﹣）
＝．
故答案为：；
（2）原式＝3×（1﹣+﹣+﹣+•••+）
＝3×（1﹣）
＝3×
＝．
故答案为：；
（3）原式＝﹣1+﹣+﹣+•••+﹣
＝﹣1．
故答案为：﹣1．
【点评】本题考查的是实数的运算，根据题意找出运算规律是解题的关键．
24．“数形结合”是重要的数学思想．如：|3﹣（﹣2）|表示3与﹣2差的绝对值，实际上也可以理解为3与﹣2在数轴上所对应的两个点之间的距离．进一步地，数轴上两个点A，B所对应的数分别用a，b表示，那么A，B两点之间的距离表示为AB＝|a﹣b|．利用此结论，回答以下问题：

（1）数轴上﹣2和5这两点之间的距离为 　7　．
（2）若x表示一个实数，|x+2|+|x﹣4|的最小值为 　6　．
（3）直接写出所有符合条件的x，使得|x﹣2|+|x+5|＝9，则x的值为 　3或﹣6　．
【分析】（1）利用数轴直观得出答案．
（2）x在﹣2到4之间值最小，两点之间线段最短．
（3）2到﹣5之间是7，与9相差2，分到两段中，每段加1，得出结果．
解：（1）|（﹣2）﹣5|＝7．
（2）当x＜﹣2时，|x+2|+|x﹣4|＝﹣2x+2＞6；
当﹣2≤x≤4时，|x+2|+|x﹣4|＝6；
当x＞4时，|x+2|+|x﹣4|＝2x﹣2＞6，
故|x+2|+|x﹣4|最小值为6．
（3）当x＜﹣5时，|x﹣2|+|x+5|＝﹣（x﹣2）﹣（x+5）＝﹣2x﹣3＝9，
解方程得：x＝﹣6；
当﹣5≤x≤2时，|x﹣2|+|x+5|＝7，无解；
当x＞2时，|x﹣2|+|x+5|＝2x+3＝9，
解方程得：x＝3．
故x的值为﹣6或3．
【点评】本题考查了数轴上两点间的距离，绝对值的几何意义，解本题的关键是分段讨论．