中考数学复习第12课时二次函数的图象和性质课堂教学课件

这是一份中考数学复习第12课时二次函数的图象和性质课堂教学课件，共44页。PPT课件主要包含了要点知识，福建6年中考聚焦，y＝－x－22，答案不唯一，图象和性质，题串考点，1－4，直线x＝1，0－3，m≥1等内容，欢迎下载使用。

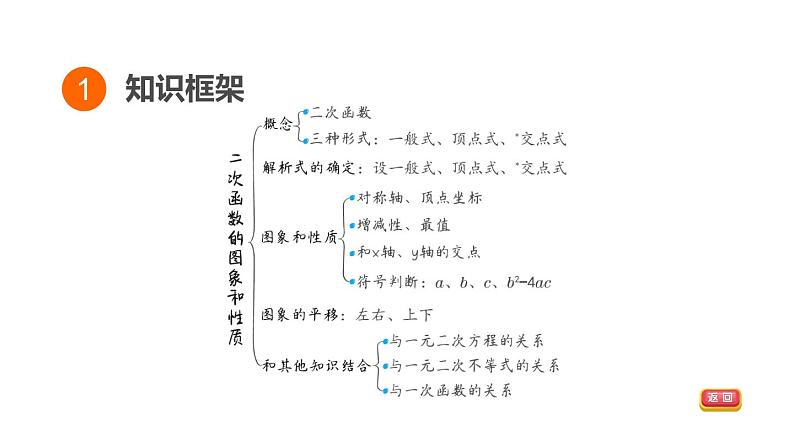
· 考点1 二次函数概念及解析式的确定
· 考点2 二次函数的图象和性质
· 考点3 二次函数图象的平移
· 考点4 二次函数和其他知识的结合
考点1 二次函数概念及解析式的确定
1．概念：一般地，形如y＝ax2＋bx＋c(a，b，c，是常数，a≠0)的函数叫做二次函数.2．解析式的确定：(1)已知抛物线上三点坐标或三组x，y的对应值→设一般式：y＝ax2＋bx＋c(a≠0)；
(2)已知抛物线的顶点坐标或对称轴或最值→设顶点式：y＝a(x－h)2＋k(a≠0)；(3)已知抛物线与x轴的两个交点坐标A(x1，0)，B(x2，0)→设交点式：y＝a(x－x1)(x－x2) (a≠0).
1．【2022福州质检4分】下列y关于x的函数中，是二次函数的是(　　)A．y＝5x2B．y＝22－2xC．y＝2x2－3x3＋1 D．y＝
2．【2022莆田模拟4分】写出一个满足“当x＞2时，y随x增大而减小”的二次函数解析式：____________.
3．【2021永安模拟4分】在平面直角坐标系xOy中，关于x的二次函数y＝x2＋px＋q的图象过点(－1，0)，(2，0)，求这个二次函数的解析式.
考点2 二次函数的图象和性质
2. a，b，c符号的确定：
已知二次函数y＝x2－2x－3.(1)该函数的图象的开口向_____，顶点坐标为________，对称轴为___________，与y轴的交点坐标为____________，与x轴的交点坐标为___________________.
(－1，0)，(3，0)
(2)在如图所示的平面直角坐标系内画出该函数的图象，并填空：①当x________时，y随x的增大而增大；当x________时，y随x的增大而减小.
【变式练习】若x≥m时， y随x的增大而增大，则m的取值范围是____________.②当0≤x≤4时，函数y的最小值是________，最大值是________.
【变式练习】若0≤x≤m时，函数y的最小值是－4，最大值是－3，则m的取值范围是__________.③A(x1，y1)，B(x2，y2)是该抛物线上的两点，若y1＝y2，则x1＋x2＝________.
1．【2022南平延平区模拟4分】如图，抛物线y＝ax2＋bx＋c的对称轴是直线x＝1，下列结论：①abc＞0；②b2－4ac＞0；③a－b＋c＞0；④8a＋c＜0.正确的有(　　)A．4个 B．3个 C．2个 D．1个
福建6年中考聚焦[6年4考]
2．【2019福建4分】若二次函数y＝|a|x2＋bx＋c的图象过不同的五点A(m，n)，B(0，y1)，C(3－m，n)，D( ，y2)，E(2，y3)，则y1，y2，y3的大小关系是(　　)A．y1＜y2＜y3 B．y1＜y3＜y2C．y3＜y2＜y1 D．y2＜y3＜y1
3．【2020福建4分】已知P1(x1，y1)，P2(x2，y2)是抛物线y＝ax2－2ax上的点，下列命题正确的是(　　)A．若|x1－1|>|x2－1|，则y1>y2B．若|x1－1|>|x2－1|，则y1【点拨】∵抛物线y＝ax2－2ax＝a(x－1)2－a，∴该抛物线的对称轴是直线x＝1，当a＞0时，若|x1－1|＞|x2－1|，则y1＞y2，故选项B错误；当a＜0时，若|x1－1|＞|x2－1|，则y1＜y2，故选项A错误；若|x1－1|＝|x2－1|，则y1＝y2，故选项C正确；若y1＝y2，则|x1－1|＝|x2－1|，故选项D错误．故选C.
4．【2021福建4分】二次函数y＝ax2－2ax＋c(a＞0)的图象过A(－3，y1)，B(－1，y2)，C(2，y3)，D(4，y4)四个点，下列说法一定正确的是(　　)A．若y1y2＞0，则y3y4＞0B．若y1y4＞0，则y2y3＞0C．若y2y4＜0，则y1y3＜0D．若y3y4＜0，则y1y2＜0
5．【2022福建4分】已知抛物线y＝x2＋2x－n与x轴交于A，B两点，抛物线y＝x2－2x－n与x轴交于C，D两点，其中n＞0.若AD＝2BC，则n的值为________.
考点3 二次函数图象的平移
平移规律：左加右减，上加下减(左右移x变，上下移y变).注：可转换为顶点的平移来考虑.
已知抛物线y＝(x－1)2－4.(1)若将抛物线y＝(x－1)2－4向左平移1个单位长度，得到的抛物线的解析式为________________；(2)若将抛物线y＝(x－1)2－4向上平移3个单位长度，得到的抛物线的解析式为__________________.
1．【2022漳州质检4分】抛物线y＝x2通过平移，得到抛物线y＝x2＋1，则关于该平移方式正确的是(　　)A．向上平移1个单位长度 B．向下平移1个单位长度C．向左平移1个单位长度 D．向右平移1个单位长度
2．【2022南平质检4分】在平面直角坐标系中，抛物线y＝2x2保持不动，将x轴向上平移1个单位长度(y轴不动)，则在新坐标系下抛物线的解析式是(　　)A．y＝2x2＋1 B．y＝2x2－1 C．y＝2(x－1)2 D．y＝2(x＋1)2
3．【2022福州质检4分】将抛物线y＝x2沿直线y＝3x方向移动 个单位长度，若移动后抛物线的顶点在第一象限，则移动后抛物线的解析式是______________.
考点4 二次函数和其他知识的结合
1．与一元二次方程的关系：方程ax2＋bx＋c＝0(a≠0)的解就是抛物线y＝ax2＋bx＋c与x轴交点的横坐标的值，则有：Δ＞0⇔抛物线与x轴有两个交点；Δ＝0⇔抛物线与x轴有一个交点；Δ＜0⇔抛物线与x轴没有交点.
2．与一元二次不等式的关系(结合图象进行理解)：
3.与一次函数的关系：
已知二次函数y＝ax2＋bx＋c的图象经过点A(－1，0)和B(3，0).(1)关于x的方程ax2＋bx＋c＝0的解是________________；当a>0时，关于x的不等式ax2＋bx＋c>0的解集是_____________；
(2)当c＝－3时，若直线BC的解析式为y＝kx－3，则关于x的方程ax2＋(b－k)x＝0的解是_____________；关于x的不等式ax2＋(b－k)x＜0的解集是____________；(3)当c＝－3时，若关于x的方程ax2＋bx－3＝t在0≤x≤4有解，则t的取值范围是____________.
1．【2022福州质检4分】二次函数y＝x2＋(a＋2)x＋a(a为常数)的图象与x轴交点的情况是(　　)A．没有交点 B．有一个交点 C．有两个交点 D．与a的值有关
2．【2022南平模拟4分】如图，抛物线y＝ax2与直线y＝bx＋c的两个交点的坐标分别为A(－4，8)，B(2，2)，则关于x的方程ax2－bx－c＝0的解为__________________.
1．已知抛物线y＝ax2＋bx＋c上的部分点的横坐标x与纵坐标y的对应值如表：
以下结论正确的是(　　)A．抛物线y＝ax2＋bx＋c的开口向下B．当x＜3时，y随x增大而增大C．方程ax2＋bx＋c＝0的根为0和2D．当y＞0时，x的取值范围是0＜x＜2
2．抛物线y＝2x2－4x＋5的对称轴是直线________，顶点坐标是__________.
3．在平面直角坐标系xOy中，若抛物线y＝x2＋2x＋k与x轴只有一个交点，则k＝________.
4．设抛物线y＝x2＋(a＋1)x＋a，其中a为实数.(1)若抛物线经过点(－1，m)，则m＝______；(2)将抛物线y＝x2＋(a＋1)x＋a向上平移2个单位长度，所得抛物线顶点的纵坐标的最大值是________.
5．【2022仙游质检8分】已知二次函数y＝ax2＋b的图象与直线y＝x＋1相交于点A(2，m)和点B(n，0).(1)求二次函数的解析式；