第三章 函数的奇偶性的概念、判断或证明练习---2022-2023学年高一数学人教A版（2019）必修一重难点突破

函数的奇偶性的概念、判断或证明

一、单选题（本大题共4小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1.     已知函数，有以下结论：

①的图象关于原点对称；

②的图象关于y轴对称；

③在R上单调递增；

④的值域为

其中所有正确结论的序号是(    )

A. ② B. ①④ C. ②④ D. ①③④

2.    函数是奇函数的充要条件是(    )

A.  B.  C.  D.

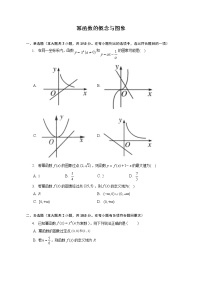
3.    设函数，则下列函数中为奇函数的是(    )

A.  B.  C.  D.

4.    定义在区间的奇函数为增函数；偶函数在区间的图象与的图象重合，设，给出下列不等式：
   ①；
   ②；
   ③；
   ④，
   其中成立的是(    )

A. ①与④ B. ②与③ C. ①与③ D. ②与④

二、多选题（本大题共3小题，共15.0分。在每小题有多项符合题目要求）

5.    已知函数，，则(    )

A. 是增函数 B. 是偶函数 C.  D.

6.    关于函数的性质描述，正确的是(    )

A. 的定义域为 B. 的值域为
C. 的图象关于原点对称 D. 在定义域上是增函数

7.    已知函数是定义在R上的奇函数，则下列函数中为奇函数的是(    )

A.  B.  C.  D.

三、填空题（本大题共3小题，共15.0分）

8.    已知是奇函数，是偶函数，它们的定义域为，且它们在上的图象如图所示，则函数是__________填“奇函数、偶函数、既是奇函数又是偶函数、既不是奇函数又不是偶函数”中的一个；不等式的解集是__________.

9.    设偶函数的定义域为，当时，的图象如图所示，则不等式的解是__________.

10. 已知偶函数的定义域为，且在区间上的图象如图所示，则的x的取值范围是__________.

四、解答题（本大题共3小题，共36.0分。解答应写出文字说明，证明过程或演算步骤）

11. 本小题分
    已知函数是定义在区间上的奇函数，且
    用定义法证明函数在区间上单调递增;
    设，求证：是偶函数，是奇函数.
12. 本小题分
    已知函数
    若函数的图象过点，求实数m的值，并证明函数为奇函数；
    若，用单调性的定义证明函数在上单调递增.
13. 本小题分

已知函数是定义在R上的偶函数，且当时，现已画出函数在y轴左侧的图象，如图所示.

请补充完整函数的图象；

根据图象写出使的x的取值范围.

当时，请写出的表达式.

答案和解析

1.【答案】C 

【解析】

【分析】

本题考查了函数的奇偶性和单调性以及函数的值域，属于中档题.
易得函数为奇函数，可判断①②，，通过判断的单调性，得出的单调性，可判断③，结合可得可判断④，从而得出结果.

【解答】

解：的定义域为 R，

，即函数为偶函数，

函数的图象关于y轴对称，故①不正确，②正确；

，

又由复合函数的单调性可知函数在上单调递增，在上单调递减，
函数在上单调递减，在上单调递增，故③不正确；

，
 

即函数的值域为故④正确.
故选

2.【答案】C 

【解析】

【分析】

本题考查判断函数的奇偶性和充要条件及其判断，属于中档题．
若是奇函数，则恒成立，根据恒等式成立的条件即可求得a、b的值．

【解答】

解：若是奇函数，则，
即恒成立，
恒成立，
要使上式恒成立，只需，即，
故函数是奇函数的充要条件是
故选

3.【答案】B 

【解析】

【分析】

本题考查了函数奇偶性和函数的图象变换，解题的关键是确定的对称中心，考查了逻辑推理能力，属于中档题．
先根据函数的解析式，得到的对称中心，然后通过图象变换，使得变换后的函数图象的对称中心为，从而得到答案．

【解答】

解：因为，
所以函数的对称中心为，
所以将函数向右平移一个单位，向上平移一个单位，
得到函数，该函数的对称中心为，
故函数为奇函数．
故选：

4.【答案】C 

【解析】

【分析】

根据，，，，对①②③④进行逐一验证即可得答案．
本题主要考查函数奇偶性的应用．

【解答】

解：由题意知，
又，，，；
①，
故①对②不对．
③，
故③对④不对．
故选

5.【答案】ABD 

【解析】

【分析】

本题考查分段函数单调性的判定，考查函数值的求法，属于中档题．
分别判断两段函数的单调性，再结合端点值间的关系判断A；由偶函数的定义判断B；求解函数值判断C与

【解答】

解：当时，，函数在上为增函数，且，
当时，，其对称轴为，在上单调递增，且
是增函数，故A正确；
函数的定义域为R，且，
是偶函数，故B正确；
，
，故C错误；
，
，故D正确．
故选

6.【答案】ABC 

【解析】

【分析】

本题考查分段函数的图象与性质的应用问题，函数的定义域和值域的应用问题，属于中档题.
化简函数，对选项中的结论进行分析判断即可．

【解答】

解：对于A：要使函数有意义可得，解得且，
故函数的定义域为故A正确;
对于B：，
在上单调递增，，
在上单调递增，，
所以值域为，故B正确;
对于C：当，，所以，
同理时，，
综上所述：，函数的图象关于原点对称，故C正确，
对于D：函数在上单调递增，在上单调递增，但是在x轴左侧的函数值比右侧的函数值大，所以在定义域上不是增函数，故D不正确;
故选：

7.【答案】AB 

【解析】

【分析】

本题主要考查函数的奇偶性，属于中档题．
根据为奇函数，可得，再逐项分析可得结果．

【解答】

解：因为函数是定义在R上的奇函数，
所以，
对于A：，故A为奇函数；
对于B：，故B为奇函数；
对于C：，故C为偶函数；
对于D：定义域是没有奇偶性，
故选

8.【答案】奇函数

【解析】

【分析】

本题主要考查函数的奇偶性在解不等式中的应用，还考查了数形结合，转化，等思想方法
首先由是偶函数，是奇函数，得到是奇函数，再将不等式转化为，观察图象选择函数值异号的部分，从而求得答案

【解答】

 解：为奇函数，为偶函数，，，
，为奇函数；
由题图可知当时，与异号，
的解集为
故答案为：奇函数；

9.【答案】 

【解析】

【分析】

本题考查利用函数的奇偶性求解不等式，属于中档题.
由为偶函数可以补全函数在上的图象，结合图象可解得不等式的解集.

【解答】

解：因为为偶函数，所以可以补全函数在上的图象，如图，

由，得：
当时，，得；
当时，，得， 
综上：不等式的解是
故答案为

10.【答案】 

【解析】

【分析】

本题考查奇偶函数图像特征的应用，属于较易题.
根据偶函数的图象关于y轴对称画出函数图象即可解.

【解答】

解：是偶函数，
其图象关于y轴对称，
由在上的图象作出在上的图象，
如图，得到在上的图象．

的x的取值范围为
故答案为

11.【答案】解：为定义在区间上的奇函数，
，
又，
检验：当，时，，，
为奇函数，符合题意，

对任意的，

，
，，
又，，
函数在区间上单调递增;
易知定义在，由于，因此也必有
可见的定义域也是若设，
则与的定义域也是

，
所以为偶函数，为奇函数，
即是偶函数，是奇函数. 

【解析】本题考查定义法证明函数单调性，奇偶性，属于中档题.
 

12.【答案】解：根据题意，函数的图象过点，
则有，解可得，则，
其定义域为，关于原点对称，
且，
则函数为奇函数
证明：若，则，
设，
则，
又由，则，，
则，即，
则函数在上为增函数． 

【解析】由的图象过点可求得m的值，利用函数奇偶性的定义即可证明函数为奇函数；
利用单调性的定义即可得证．
本题主要考查函数的奇偶性与单调性的证明．
 

13.【答案】解：因为函数为偶函数，故图象关于y轴对称，补出完整函数图象如图所示：

解：由图象得的x的取值范围为

解：设，则，所以，
因为是定义在R上的偶函数，所以，

所以时，

【解析】本题主要考查奇偶函数的图像特征，考查函数的单调性和单调区间，考查利用奇偶性求函数的解析式，属于中档题.

由函数为偶函数，图象关于y轴对称，故直接补出完整函数的图象即可;

由图象直接可写出的x的取值范围；

直接利用偶函数的性质求解析式.