2018-2022年北京中考数学5年真题1年模拟汇编 专题12 三角形全等（学生卷+教师卷）

这是一份2018-2022年北京中考数学5年真题1年模拟汇编 专题12 三角形全等（学生卷+教师卷），文件包含专题12三角形全等5年20182022中考1年模拟数学分项汇编北京专用解析版docx、专题12三角形全等5年20182022中考1年模拟数学分项汇编北京专用原卷版docx等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
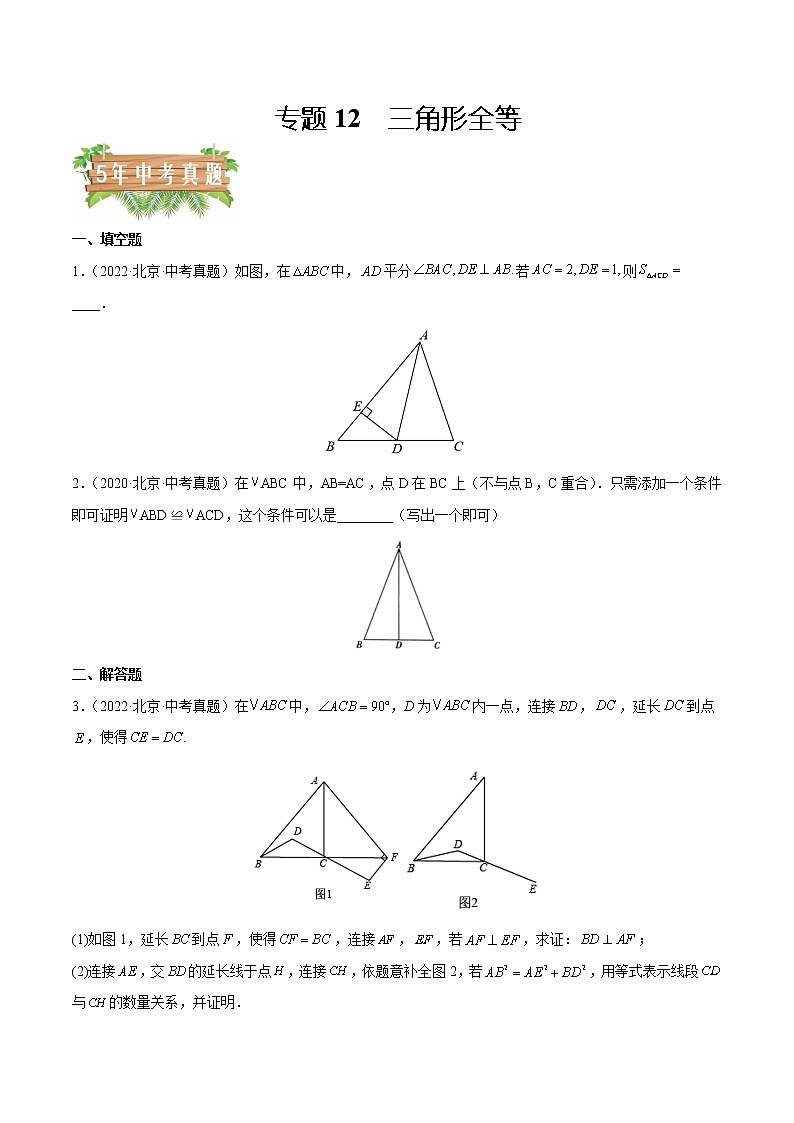
专题12  三角形全等一、填空题1．（2022·北京·中考真题）如图，在中，平分若则____．2．（2020·北京·中考真题）在ABC中，AB=AC，点D在BC上（不与点B，C重合）．只需添加一个条件即可证明ABD≌ACD，这个条件可以是________（写出一个即可）二、解答题3．（2022·北京·中考真题）在中，，D为内一点，连接，，延长到点，使得(1)如图1，延长到点，使得，连接，，若，求证：；(2)连接，交的延长线于点，连接，依题意补全图2，若，用等式表示线段与的数量关系，并证明．4．（2022·北京·中考真题）在平面直角坐标系中，已知点对于点给出如下定义：将点向右或向左平移个单位长度，再向上或向下平移个单位长度，得到点，点关于点的对称点为，称点为点的“对应点”．(1)如图，点点在线段的延长线上，若点点为点的“对应点”．①在图中画出点；②连接交线段于点求证：(2)的半径为1，是上一点，点在线段上，且，若为外一点，点为点的“对应点”，连接当点在上运动时直接写出长的最大值与最小值的差（用含的式子表示）5．（2022·北京·中考真题）如图，是的直径，是的一条弦，连接(1)求证：(2)连接,过点作交的延长线于点，延长交于点，若为的中点，求证：直线为的切线．6．（2021·北京·中考真题）《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点处立一根杆，在地面上沿着杆的影子的方向取一点，使两点间的距离为10步（步是古代的一种长度单位），在点处立一根杆；日落时，在地面上沿着点处的杆的影子的方向取一点，使两点间的距离为10步，在点处立一根杆．取的中点，那么直线表示的方向为东西方向．（1）上述方法中，杆在地面上的影子所在直线及点的位置如图所示．使用直尺和圆规，在图中作的中点（保留作图痕迹）；（2）在如图中，确定了直线表示的方向为东西方向．根据南北方向与东西方向互相垂直，可以判断直线表示的方向为南北方向，完成如下证明．证明：在中，______________，是的中点，（______________）（填推理的依据）．∵直线表示的方向为东西方向，∴直线表示的方向为南北方向．7．（2020·北京·中考真题）在中，∠C=90°，AC＞BC，D是AB的中点．E为直线上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．（1）如图1，当E是线段AC的中点时，设，求EF的长（用含的式子表示）；（2）当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．8．（2018·北京·中考真题）如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF=GC；（2）用等式表示线段BH与AE的数量关系，并证明．一、填空题1．（2022·北京市三帆中学模拟预测）如图，平分，点B在射线上，若使，则还需添加的一个条件是_______（只填一个即可）．2．（2022·北京市第一六一中学分校一模）如图，，只需添加一个条件即可证明，这个条件可以是________（写出一个即可）3．（2022·北京海淀·一模）如图，在的正方形网格中，A，B，C，D，E是网格线交点．请画出一个，使得与全等______．4．（2022·北京市第五中学分校模拟预测）如图，已知BE＝DC，请添加一个条件，使得△ABE≌△ACD：_____．5．（2022·北京丰台·一模）如图，点B，E，C，F在一条直线上，BC＝EF，∠B＝∠DEF．只需添加一个条件即可证明△ABC≌△DEF，这个条件可以是 _____（写出一个即可）．6．（2022·北京昌平·模拟预测）如图，△ABC中，AB=10，AC=7，AD是角平分线，CM⊥AD于M，且N是BC的中点，则MN=_______．7．（2022·北京顺义·一模）.如图，在 Rt△ABC中，∠B＝90°，以点 A 为圆心，适当长为半径画弧，分别交AB、AC 于点 D，E，再分别以点 D、E 为圆心，大于DE 为半径画弧，两弧交于点F，作射线AF交边BC于点G，若 BG＝1，AC＝4，则△ACG 的面积是________.8．（2022·北京市广渠门中学模拟预测）如图，正方形是由四个全等的直角三角形围成的，若，，则的长为___．9．（2022·北京十一学校一分校一模）如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAD+∠ADC=_____．10．（2022·北京房山·二模）如图，点在直线外，点、、、均在直线上，如果，只需添加一个条件即可证明，这个条件可以是________（写出一个即可）．二、解答题11．（2022·北京昌平·模拟预测）如图，点F，C分别在线段AB，BD上，且BF＝BD，AF＝CD，连接AC，DF，并相交于点E．求证：AE＝CE．12．（2022·北京昌平·模拟预测）在菱形ABCD中，∠ABC=60°，E是对角线AC上一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．(1)若E是线段AC的中点，如图1，易证：BE=EF(不需证明)；(2)若E是线段AC或AC延长线上的任意一点，其它条件不变， 如图2、图3，线段BE、EF有怎样的数量关系，直接写出你的猜想；并选择一种情况给予证明．13．（2022·北京·模拟预测）如图，AB＝AD，AC＝AE，∠BAE＝∠DAC．求证：∠C＝∠E． 14．（2022·北京房山·一模）已知：等边△ABC，过点B作AC的平行线l．点P为射线AB上一个动点（不与点A，B重合），将射线PC绕点P顺时针旋转60°交直线l于点D．(1)如图1，点P在线段AB上时，依题意补全图形；①求证：∠BDP=∠PCB；②用等式表示线段BC，BD，BP之间的数里关系，并证明；(2)点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系．15．（2022·北京通州·一模）如图，在中，∠ACB＝90°，AC＝BC．点D是BC延长线上一点，连接AD．将线段AD绕点A逆时针旋转90°，得到线段AE．过点E作，交AB于点F．(1)①直接写出∠AFE的度数是______；②求证：∠DAC＝∠E；(2)用等式表示线段AF与DC的数量关系，并证明．16．（2022·北京丰台·一模）如图，在△ABC中，AB＝AC，∠BAC＝α，点D在边BC上（不与点B，C重合），连接AD，以点A为中心，将线段AD逆时针旋转180°﹣α得到线段AE，连接BE．(1)∠BAC+∠DAE＝　   　°；(2)取CD中点F，连接AF，用等式表示线段AF与BE的数量关系，并证明．17．（2022·北京石景山·一模）如图，△ACB中，，，D为边BC上一点（不与点C重合），，点E在AD的延长线上，且，连接BE，过点B作BE的垂线，交边AC于点F．(1)依题意补全图形；(2)求证：；(3)用等式表示线段AF与CD的数量关系，并证明．18．（2022·北京平谷·二模）如图，在△ABC中，，点D为BC边中点，过点D作DE⊥BC交AC于E，连接BE并延长使，连接FC，G为BC上一点，过G作GH⊥BF于点H，作GM⊥AC于点M．(1)依题意补全图形；(2)求证：；(3)判断线段HG、GM、FC之间的数量关系，并证明．19．（2022·北京市广渠门中学模拟预测）如图，等腰中，，点P为射线BC上一动点（不与点B、C重合），以点P为中心，将线段PC逆时针旋转角，得到线段PQ，连接、M为线段BQ的中点．(1)若点P在线段BC上，且M恰好也为AP的中点，①依题意在图1中补全图形：②求出此时的值和的值；(2)写出一个的值，使得对于任意线段BC延长线上的点P，总有的值为定值，并证明；20．（2022·北京·二模）如图，在等边中，点是边的中点，点是直线上一动点，将线段绕点逆时针旋转，得到线段，连接，．(1)如图1，当点与点重合时．①依题意补全图形；②判断与的位置关系；(2)如图2，取的中点，写出直线与夹角的度数以及与的数量关系，并证明．21．（2022·北京市第一六一中学分校一模）已知点P为线段AB上一点，将线段AP绕点A逆时针旋转60°，得到线段AC；再将线段BP绕点B逆时针旋转120°，得到线段BD；连接AD，取AD中点M，连接BM，CM．(1)如图1，当点P在线段CM上时，求证：PM//BD；(2)如图2，当点P不在线段CM上，写出线段BM与CM的数量关系与位置关系，并证明．22．（2022·北京四中模拟预测）已知，点是射线上一动点，以为边作，，，将射线绕点顺时针旋转，得到射线，点在射线上，． (1)如图1，若，求的长（用含的式子表示）；(2)如图2，点在线段上，连接、．添加一个条件：、、满足的等量关系为______，使得成立，补全图形并证明．