2018-2022年北京中考数学5年真题1年模拟汇编 专题11 三角形基础（含等腰三角形、勾股定理）（学生卷+教师卷）

这是一份2018-2022年北京中考数学5年真题1年模拟汇编 专题11 三角形基础（含等腰三角形、勾股定理）（学生卷+教师卷），文件包含专题11三角形基础含等腰三角形勾股定理5年20182022中考1年模拟数学分项汇编北京专用解析版docx、专题11三角形基础含等腰三角形勾股定理5年20182022中考1年模拟数学分项汇编北京专用原卷版docx等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。
专题11 三角形基础（含等腰三角形、勾股定理）

一、填空题
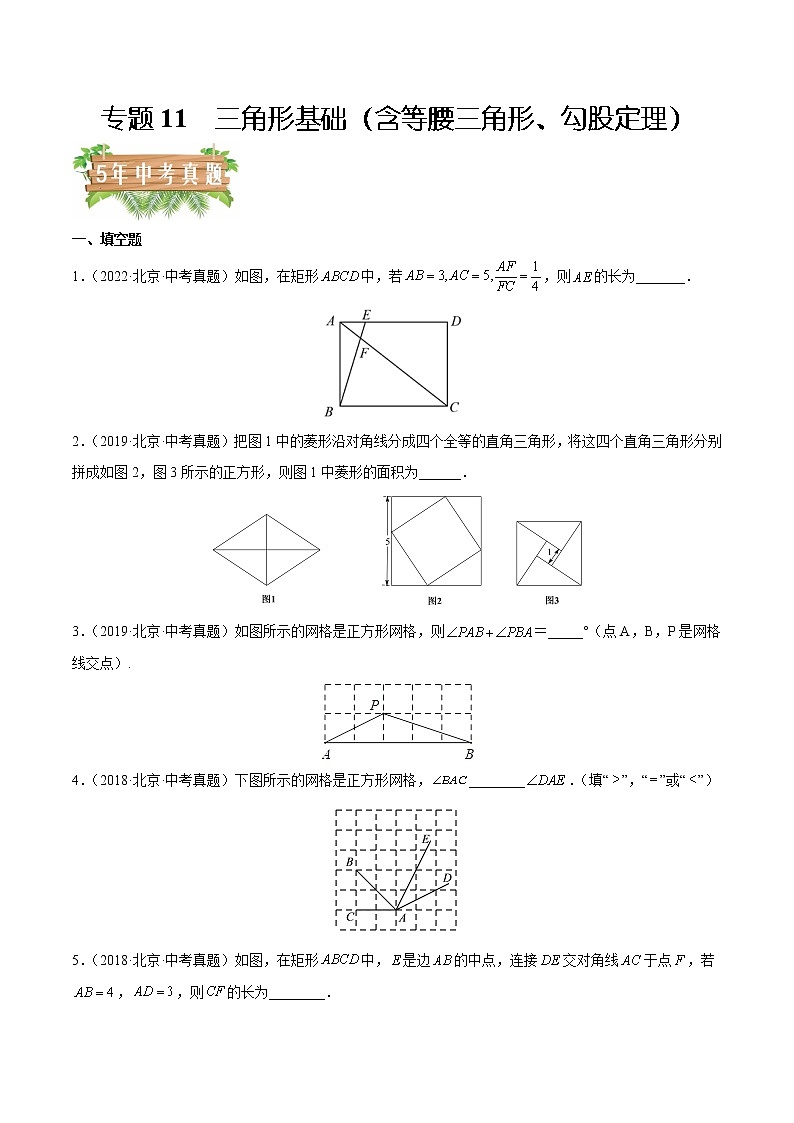
1．（2022·北京·中考真题）如图，在矩形中，若，则的长为_______．

【答案】1
【解析】解：在矩形中：，，
∴，，
∴，
∴，
故答案为：1．
2．（2019·北京·中考真题）把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为______．

【答案】12
【解析】解：如图1所示：

∵四边形ABCD是菱形，
∴OA=OC，OB=OD，AC⊥BD，
设OA=x，OB=y，
由题意得：，解得：，
∴AC=2OA=6，BD=2OB=4，
∴菱形ABCD的面积=；
故答案为12．
3．（2019·北京·中考真题）如图所示的网格是正方形网格，则＝_____°（点A，B，P是网格线交点）.

【答案】45
【解析】解：延长AP交格点于D，连接BD，

则PD2=BD2=1+22=5，PB2=12+32=10，
∴PD2+DB2=PB2，
∴∠PDB=90°，
即△PBD为等腰直角三角形，
∴∠DPB=∠PAB+∠PBA=45°，
故答案为：45．
4．（2018·北京·中考真题）下图所示的网格是正方形网格，________．（填“”，“”或“”）

【答案】>
【解析】解：如下图所示，

是等腰直角三角形，
∴，
∴．
故答案为
另：此题也可直接测量得到结果．
5．（2018·北京·中考真题）如图，在矩形中，是边的中点，连接交对角线于点，若，，则的长为________．

【答案】
【解析】解：∵四边形是矩形，
∴，//，，
在中，，
∴，
∵是中点，
∴，
∵//，
∴，
∴．
故答案为：．
二、解答题
6．（2022·北京·中考真题）在中，，D为内一点，连接，，延长到点，使得

(1)如图1，延长到点，使得，连接，，若，求证：；
(2)连接，交的延长线于点，连接，依题意补全图2，若，用等式表示线段与的数量关系，并证明．
【答案】(1)见解析
(2)；证明见解析
【解析】(1)证明：在和中，
，
∴ ，
∴ ，
∴ ，
∵，
∴．
(2)解：补全后的图形如图所示，，证明如下：

延长BC到点M，使CM＝CB，连接EM，AM，
∵，CM＝CB，
∴ 垂直平分BM，
∴，
在和中，
，
∴ ，
∴ ，，
∵，
∴ ，
∴ ，
∵，
∴ ，
∴ ，即，
∵，
∴ ，
∴ ．
7．（2021·北京·中考真题）《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点处立一根杆，在地面上沿着杆的影子的方向取一点，使两点间的距离为10步（步是古代的一种长度单位），在点处立一根杆；日落时，在地面上沿着点处的杆的影子的方向取一点，使两点间的距离为10步，在点处立一根杆．取的中点，那么直线表示的方向为东西方向．
（1）上述方法中，杆在地面上的影子所在直线及点的位置如图所示．使用直尺和圆规，在图中作的中点（保留作图痕迹）；

（2）在如图中，确定了直线表示的方向为东西方向．根据南北方向与东西方向互相垂直，可以判断直线表示的方向为南北方向，完成如下证明．
证明：在中，______________，是的中点，
（______________）（填推理的依据）．
∵直线表示的方向为东西方向，
∴直线表示的方向为南北方向．
【答案】（1）图见详解；（2），等腰三角形的三线合一
【解析】解：（1）如图所示：

（2）证明：在中，，是的中点，
（等腰三角形的三线合一）（填推理的依据）．
∵直线表示的方向为东西方向，
∴直线表示的方向为南北方向；
故答案为，等腰三角形的三线合一．
8．（2021·北京·中考真题）在平面直角坐标系中，的半径为1，对于点和线段，给出如下定义：若将线段绕点旋转可以得到的弦（分别是的对应点），则称线段是的以点为中心的“关联线段”．

（1）如图，点的横､纵坐标都是整数．在线段中，的以点为中心的“关联线段”是______________；
（2）是边长为1的等边三角形，点，其中．若是的以点为中心的“关联线段”，求的值；
（3）在中，．若是的以点为中心的“关联线段”，直接写出的最小值和最大值，以及相应的长．
【答案】（1）；（2）；（3）当时，此时；当时，此时．
【解析】解：（1）由题意得：

通过观察图象可得：线段能绕点A旋转90°得到的“关联线段”，都不能绕点A进行旋转得到；
故答案为；
（2）由题意可得：当是的以点为中心的“关联线段”时，则有是等边三角形，且边长也为1，当点A在y轴的正半轴上时，如图所示：

设与y轴的交点为D，连接，易得轴，
∴，
∴，，
∴，
∴；
当点A在y轴的正半轴上时，如图所示：

同理可得此时的，
∴；
（3）由是的以点为中心的“关联线段”，则可知都在上，且，则有当以为圆心，1为半径作圆，然后以点A为圆心，2为半径作圆，即可得到点A的运动轨迹，如图所示：

由运动轨迹可得当点A也在上时为最小，最小值为1，此时为的直径，
∴，
∴，
∴；
由以上情况可知当点三点共线时，OA的值为最大，最大值为2，如图所示：

连接，过点作于点P，
∴，
设，则有，
∴由勾股定理可得：，即，
解得：，
∴，
∴，
在中，，
∴；
综上所述：当时，此时；当时，此时．
9．（2020·北京·中考真题）在中，∠C=90°，AC＞BC，D是AB的中点．E为直线上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．
（1）如图1，当E是线段AC的中点时，设，求EF的长（用含的式子表示）；
（2）当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．

【答案】（1）；（2）图见解析，，证明见解析．
【解析】（1）∵D是AB的中点，E是线段AC的中点
∴DE为的中位线，且
∴，
∵
∴
∵
∴
∴四边形DECF为矩形
∴

∴
则在中，；
（2）过点B作AC的平行线交ED的延长线于点G，连接FG
∵
∴，
∵D是AB的中点
∴
在和中，
∴
∴，
又∵
∴DF是线段EG的垂直平分线
∴
∵，
∴
在中，由勾股定理得：
∴．

10．（2018·北京·中考真题）如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．
（1）求证：GF=GC；
（2）用等式表示线段BH与AE的数量关系，并证明．

【答案】（1）证明见解析；（2）BH=AE，理由见解析
【解析】（1）证明：连接．
∵，关于对称．
∴．．

在和中
，
∴，
∴．
∵四边形是正方形，
∴．，
∴，
∴，
∴ ，
∵，，
∴．
在和中
．
∴≌，
∴．
（2）．
证明：在上取点使得，连接．
∵四这形是正方形．
∴，．

∵≌，
∴．
同理：，
∴
∵，
∴，
∴，
∴．
∴．
∵，
∴．
∵，
∴，
∴．
∵，，
∴．
在和中，
∴≌，
∴，
在中，，．
∴，
∴．
11．（2018·北京·中考真题）如图，在四边形中，AB//DC，，对角线，交于点，平分，过点作交的延长线于点，连接．
（1）求证：四边形是菱形；
（2）若，，求的长．

【答案】（1）证明见解析；（2）OE=2．
【解析】（1）证明：∵AB//CD，
∴，
∵平分，
∴，
∴，
∴，
又∵，
∴，
又∵∥，
∴四边形是平行四边形，
又∵，
∴是菱形．
（2）解：∵四边形是菱形，对角线、交于点，
∴，，，
∴，
在Rt△AOB中，，
∴，
∵，
∴，
在Rt△AEC中，，为中点，
∴．

一、填空题
1．（2022·北京四中模拟预测）如图，⊙O的直径AB垂直于弦CD，垂足为E，∠CAD＝45°，则∠BOC＝_____°．

【答案】45
【解析】解：∵⊙O的直径AB垂直于弦CD，
∴CE＝DE，
∴ AB垂直平分CD
∴AC＝AD
∴△ACD是等腰三角形
∴∠BAC＝∠CAD＝×45°＝22.5°
∴∠BOC＝2∠BAC＝45°，
故答案为：45．
2．（2022·北京房山·一模）如图，点A，B，C在⊙O上，若∠OCB=20°，则∠A度数为_________．

【答案】70°
【解析】解：∵OB＝OC，∠OCB＝20°，
∴∠OBC＝∠OCB＝20°，
∴∠BOC＝180°―∠OBC―∠OCB＝180°﹣20°﹣20°＝140°，
∴∠A＝∠BOC＝70°
故答案为：70°
3．（2022·北京市燕山教研中心一模）是平面直角坐标系中的两点，线段长度的最小值为____________．
【答案】3
【解析】解：∵A（a，0），B（5，3），
∴，
当，即时，线段AB的长度的值最小，
此时，
故答案为：3．
4．（2022·北京门头沟·一模）石拱桥是中国传统桥梁四大基本形式之一，如图，已知一石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，求水面宽AB＝_____m．

【答案】8．
【解析】连结OA，

拱桥半径OC为5cm，
cm，
m，
cm，
m
m，
故答案为：8．
5．（2022·北京师大附中模拟预测）如图，在矩形ABCD中，AB＝3，BC＝10，点E在边BC上，DF⊥AE，垂足为F，若DF＝6，则线段EF的长为_____．

【答案】3
【解析】解：∵四边形ABCD为矩形，
∴AB＝CD＝3，BC＝AD＝10，，
∴∠AEB＝∠DAF，
∴△AFD∽△EBA，
∴，
∵DF＝6，
∴，
∴，
∴AE＝5，
∴EF＝AF－AE＝8－5＝3，
故答案为：3．
6．（2022·北京房山·一模）如图，在△ABC 中，AB＝AC，AB 的垂直平分线 MN 交 AC 于 D 点．若 BD 平分∠ABC，则∠A＝________________   °．

【答案】36
【解析】∵AB＝AC，
∴∠C＝∠ABC，
∵AB的垂直平分线MN交AC于D点．
∴∠A＝∠ABD，
∵BD平分∠ABC，
∴∠ABD＝∠DBC，
∴∠C＝2∠A＝∠ABC，
设∠A为x，
可得：x+x+x+2x＝180°，
解得：x＝36°，
故答案为36．
7．（2022·北京朝阳·模拟预测）已知如图，在ABC中，BAE=CAE,BEAE于点E，若ABC=3ACB,则AB,AC,BE之间的数量关系____________．

【答案】
【解析】
【分析】
延长BE交AC于点F，证明AF=AB，得AC-AB=CF，再证明CF=BF=2BE即可得到结论．
【详解】
如图，延长BE交AC于点F，

∵AE⊥BE，
∴∠AEB=∠AEF=90︒，
在△AEB中，∵∠ABE+∠BAE+∠AEB=180︒，
∴∠ABE=90︒-∠BAE，
同理，∠AFE=90︒-∠FAE，
∵∠BAE=∠FAE，
∴∠ABE=∠AFE，
∴AB=AF，
∵AE⊥BE，
∴BF=2BE，
∴AC-AB=AC-AF=CF，
∵∠AFB是△BCF的外角，
∴∠AFB=∠FBC+∠C
∵∠ABC=3∠C
∴∠ABC=∠ABF+∠CBF=∠AFB+∠CBF，
∴3∠C=∠AFB+∠CBF=2∠CBF+∠C
∴∠CBF=∠C
∴BF=CF
∴AC-AB=BF=2BE，即
故答案为：．
8．（2022·北京十一学校一分校一模）如图，PA，PB分别切半径为1的⊙O于A，B两点，BC为直径，若，则PB的长为_____．

【答案】
【解析】解：连接OP，OA，如图：

∵PA，PB是⊙O的切线，
∴，
在和中，

∴，
∴，
∵，
∴，
∵，
∴，，
故答案为：．
9．（2022·北京通州·一模）如图，PA，PB是的切线，切点分别为A，B，连接OB，AB．如果，那么∠P的度数为______．

【答案】40°
【解析】解：∵PA、PB是⊙O的切线，
∴OB⊥BP，PA=PB，
∴∠OBP=90°，
∵，
∴∠ABP=70°，
∵PA=PB，，
∴∠BAP=∠ABP=70°，
∴∠P=180°-∠BAP-∠ABP=180°-70°-70°=40°，
故答案为：40°
10．（2022·北京房山·二模）如图，点在直线外，点、、、均在直线上，如果，只需添加一个条件即可证明，这个条件可以是________（写出一个即可）．

【答案】∠A＝∠ B
【解析】解：条件是∠A＝∠ B
理由是：∵∠A＝∠ B
∴PA＝PB
在和中，

∴（SAS）
故答案为：∠A＝∠ B
11．（2022·北京市燕山教研中心一模）如图，在中，点D、E分别、上的点，与交于点O．给出下列三个条件：①；②；③．利用其中两个条件可以证明是等腰三角形，这两个条件可以是____________．

【答案】①③或②③
【解析】当、时
在和中

∴
∴，
∵，
∴
在和中


∴
∴是等腰三角形，即①③可以证明是等腰三角形；
当、时
在和中

∴
∴，，
∵，
∴
在和中


∴
∴是等腰三角形，即②③可以证明是等腰三角形；
故答案为：①③或②③．
12．（2022·北京顺义·一模）如图，矩形ABCD中，AB=2，BC=1，将矩形ABCD绕顶点C顺时针旋转90°，得到矩形EFCG，连接AE，取AE的中点H，连接DH，则_______．

【答案】
【解析】如图，延长DH交EF于点k，

∵H是的中点

又





则

故答案为：
13．（2022·北京昌平·模拟预测）已知三角形三边长分别为6，8，10，则此三角形的面积为__________ ．
【答案】24
【解析】∵62+82=102，
∴此三角形为直角三角形，
∴此三角形的面积为：．
故答案为：24．
14．（2022·北京·中国人民大学附属中学分校一模）如图，在矩形ABCD中，点E在边CD上，将矩形ABCD沿AE所在直线折叠，点D恰好落在边BC上的点F处．若AB=8，DE=5，则折痕AE的长为________．

【答案】
【解析】解：∵四边形ABCD是长方形，
∴∠C=90°，AB=CD，AD=BC，
由折叠的性质可得：EF=DE=5，AD=AF，
∴CE=CD-DE=3，
在Rt△CEF中，CF=．
∴设AD=BC=AF=x，则BF=x-4，
∴在Rt△ABF中， ，
解得：x=10，
∴在Rt△ADE中，AE=．
故答案为5．
15．（2022·北京·模拟预测）勘测队按实际需要构建了平面直角坐标系，并标示了A，B，C三地的坐标，数据如图（单位：km）．笔直铁路经过A，B两地．
（1）A，B间的距离为______km；
（2）计划修一条从C到铁路AB的最短公路l，并在l上建一个维修站D，使D到A，C的距离相等，则C，D间的距离为______km．

【答案】     20     13
【解析】（1）由A、B两点的纵坐标相同可知：AB∥x轴，∴AB=12﹣（﹣8）=20；
（2）过点C作l⊥AB于点E，连接AC，作AC的垂直平分线交直线l于点D，由（1）可知：CE=1﹣（﹣17）=18，AE=12，设CD=x，∴AD=CD=x，由勾股定理可知：x2=（18﹣x）2+122，∴解得：x=13，∴CD=13．
故答案为（1）20；（2）13．

16．（2022·北京·二模）在平面直角坐标系xOy中，已知点Q（5，2），Z（5，3），⊙Q的半径为1，直线l：y＝ax，给出下列四个结论：
①当a＝1时，直线l与⊙Q相离；
②若直线l是⊙Q的一条对称轴，则；
③若直线l与⊙Q只有一个公共点T，则；
④若直线l上存在点Y，⊙Q上存在点C，使得∠ZYC＝90°，则a的最大值为．
其中所有正确结论的序号是 _____．
【答案】①②③④
【解析】解：如图：

①当a＝1时，直线l为y＝x，如图，直线l与⊙Q相离，则①正确；
②若直线l是⊙Q的一条对称轴，则一定过圆心，故将Q（5，2）代入y＝ax，
可得，则②正确；
③若直线l与⊙Q只有一个公共点T，则直线l与⊙Q相切，如图中
由题意得
与⊙Q相切

⊙Q的半径为1

则③正确；
④若直线l上存在点Y，⊙Q上存在点C，使得∠ZYC=90°，并使y=ax中a取得最大值，则如图，

则YZ∥x轴，YC∥y轴，
即Y（4，3），代入y=ax，得a=
则a的最大值为④正确；
故答案为：①②③④．
二、解答题
17．（2022·北京平谷·一模）如图，△ABC中，∠ACB＝90°，点D为AB边中点，过D点作AB的垂线交BC于点E，在直线DE上截取DF，使DF＝ED，连接AE、AF、BF．

(1)求证：四边形AEBF是菱形；
(2)若cos∠EBF＝，BF＝5，连接CD，求CD的长．
【答案】(1)见解析
(2)
【解析】(1)解：∵D是AB的中点，
∴AD=BD，
∵DE=DF，
∴四边形AEBF是平行四边形，
∵EF⊥AB，
∴四边形AEBF是菱形；
(2)解：∵四边形AEBF是菱形，
∴，AE=BF=BE=5，
∴∠AEC=∠EBF，
∵∠ACB=90°，
∴，
∴CE=3，
∴，BC=CE+BE=8，
∴，
∵D是AB的中点，∠ACB=90°，
∴．
18．（2022·北京东城·一模）如图，在中，，以AB为直径作，交BC于点D，交AC于点E，过点B作的切线交OD的延长线于点F．

(1)求证：；
(2)若，，求AE的长．
【答案】(1)见解析
(2)
【解析】(1)证明：






(2)解：如图：连接BE

是的直径，AB=4
，
是的切线


又


又
，解得
19．（2022·北京丰台·一模）《周髀算经》中记载了一种确定东南西北方向的方法．大意是：在平地上点A处立一根杆，记录日出时杆影子的长度AB，并以点A为圆心，以AB为半径画圆，记录同一天日落时杆影子的痕迹与此圆的交点C，那么直线CB表示的方向就是东西方向，∠BAC的角平分线所在的直线表示的方向就是南北方向．

(1)上述方法中，点A，B，C的位置如图所示，使用直尺和圆规，在图中作∠BAC的角平分线AD（保留作图痕迹）；
(2)在图中，确定了直线CB表示的方向为东西方向，根据南北方向与东西方向互相垂直，可以判断直线AD表示的方向为南北方向，完成如下证明．
证明：∵点B，C在⊙O上，
∴AB＝ ．
∴△ABC是等腰三角形．
∵AD平分∠BAC，
∴AD⊥BC （ ）（填推理的依据）．
∵直线CB表示的方向为东西方向，
∴直线AD表示的方向为南北方向．
【答案】(1)见解析
(2)AC；等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合
【解析】(1)解：如图所示，射线AD即为∠BAC的角平分线；

(2)解：证明：∵点B，C在⊙O上，
∴AB＝AC．
∴△ABC是等腰三角形．
∵AD平分∠BAC，
∴AD⊥BC （等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合）（填推理的依据）．
∵直线CB表示的方向为东西方向，
∴直线AD表示的方向为南北方向．
故答案为：AC；等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合
20．（2022·北京市燕山教研中心一模）如图，在三角形中，，，是边的高线，将线段绕点A逆时针旋转得到线段，连接交于点F．

(1)依题意补全图形，写出____________°
(2)求和的度数；
(3)用等式表示线段之间的数量关系，并证明．
【答案】(1)图见解析，°
(2)，
(3)，证明见解析
【解析】(1)解：如图分别以A，C为圆心，以AC为半径作弧，两弧交于点E，连接BE交AD于点F，则∠CAE=60°；

(2)解：∵，是边的高线，
∴，
∵线段绕点A逆时针旋转得到线段，
∴，又，
∴，
在中，，
∴
∴
又∵是边的高线，∴
∵∠BFD=∠BAF+∠ABF，
∴．
(3)解：如图，在EF上取点M，使EM=BF，连接AM，

∵AB=AE，∠ABF=∠AEM，BF=EM，∴△ABF≌△AEM（SAS），
∴AF=AM，∠BAF=∠EAM，
∵∠DAC=∠BAF，∴∠DAC=∠EAM，
∵∠CAE=60°，∴∠FAM=60°，
∴△AFM是等边三角形，
∴FM=AF，
∴AF+BF=EF；
21．（2022·北京门头沟·一模）如图，在等边中，将线段绕点顺时针旋转，得到线段．连接，作的平分线，交于．

(1)①根据题意，补全图形；
②请用等式写出与的数量关系，并证明．
(2)分别延长和交于点，用等式表示线段，，的数量关系，并证明．
【答案】(1)①见解析，②∠BAD＝2∠BCD，证明见解析；
(2)＝＋，证明见解析．
【解析】(1)解：①补全图形如图1，

② ∠BAD＝2∠BCD
证明：由旋转的性质可知AD＝AC，∠CAD＝，
∴ △ADC是等腰三角形
∴∠ADC＝∠ACD＝（180°－∠CAD）＝（180°－）＝90°－
∵△ABC是等边三角形
∴∠BAC＝∠ACB＝60°，AB＝BC＝AC＝AD
∴∠BCD＝∠ADC－∠ACB＝（90°－）－60°＝30°－
∵∠BAD＝∠BAC－∠CAD＝60°－＝2（30°－）
∴∠BAD＝2∠BCD
(2)解：＝＋，理由如下：
如图2，连接GF，在AF上截取FG＝DF，

∵AE平分∠BAD
∴∠BAF＝∠DAF＝∠BAD
∵AB＝AC，AC＝AD
∴AB＝AD
又∵AF＝AF
∴△ABF≌△ADF（SAS）
∴BF＝DF
∵∠BAD＝2∠BCD
∴∠BCD＝∠BAD
∴∠BCD＝∠BAF＝∠DAF
∵∠BAF＋∠ABC＋∠AEB＝180°，∠BCD＋∠CFE＋∠CEF＝180°，∠AEB＝∠CEF
∴∠CFG＝∠ABC＝60°
∴∠AFB＝∠AFD＝60°
∴∠BFC＝∠AFB＋∠AFD＝120°
∵FG＝DF
∴△DFG是等边三角形
∴DG＝DF＝BF，∠DGF＝60°，
∴∠AGD＝180°－∠DGF＝120°
∴∠AGD＝∠CFB
在△BCF和△DAG中，

∴△BCF≌△DAG（AAS）
∴CF＝AG
∴AF＝AG＋FG＝CF＋DF
即AF＝CF＋DF
22．（2022·北京朝阳·一模）在中，D是的中点，且，将线段沿所在直线翻折，得到线段，作交直线于点E．

(1)如图，若，
①依题意补全图形；
②用等式表示线段之间的数量关系，并证明；
(2)若，上述结论是否仍然成立？若成立，简述理由：若不成立，直接用等式表示线段之间新的数量关系（不需证明）．
【答案】(1)①见解析；② ，理由见解析
(2)不成立，
【解析】(1)①补全图形如图所示：

② ，理由如下：
如图，连接 ，

将线段沿所在直线翻折，得到线段，
，
又 ，
，
，
，
，
，
D是的中点，
，
，
，
即，
，
，
，
；
(2)不成立，，理由如下：

如图，连接，
将线段沿所在直线翻折，得到线段，
，
又 ，
，
，
D是的中点，
，
，
，
，
，
即，
，
，
，
，
，
，
．
23．（2022·北京市广渠门中学模拟预测）如图，AB是的直径，弦，垂足为H，E为上一点，过点E作的切线，分别交的延长线于点F，G连接AE，交CD于点P．

(1)求证：；
(2)连接AD，若，求半径．
【答案】(1)见解析
(2)
【解析】(1)证明：连接OE，

∵EF是圆的切线，
∴OE⊥EF．
∴∠OEF=90°．
∴∠OEA+∠AEF=90°．
∵CD⊥AB，
∴∠AHC=90°．
∴∠OAE+∠APH=90°．
∵OA=OE，
∴∠OAE=∠OEA．
∴∠AEF=∠APH．
∵∠APH=∠EPF，
∴∠EPF=∠AEF．
∴EF=PF．
(2)连接OD，设圆的半径为r，
∵直径AB⊥CD于H，CD=8，
∴CH=DH=4．
∵AD∥FG，
∴∠ADH=∠F．
∴cos∠ADH=cosF=


∴OH=OA-AH=r-3．
在Rt△ODH中，
∴（r-3）2+42=r2．

24．（2022·北京东城·一模）对于平面直角坐标系中的点C及图形G，有如下定义：若图形G上存在A，B两点，使得为等腰直角三角形，且，则称点C为图形G的“友好点”．
(1)已知点，，在点，，中，线段OM的“友好点”是_______；
(2)直线分别交x轴、y轴于P，Q两点，若点为线段PQ的“友好点”，求b的取值范围；
(3)已知直线分别交x轴、y轴于E，F两点，若线段EF上的所有点都是半径为2的的“友好点”，直接写出d的取值范围．
【答案】(1)C1、C3
(2)1≤b3
(3)≤d≤
【解析】(1)解：如图所示，

由题意知三角形OC1M为等腰直角三角形，C1符合题意；
过C2作C2A⊥OM于A，则AM=3，C2A=4，三角形AMC2不是等腰三角形，C2不符合题意；
过C3作C3B⊥OM于B，则C3B=AB=1，三角形ABC3是等腰直角三角形，符合题意；
故答案为：C1、C3．
(2)解：分两种情况讨论，当直线PQ在C点上方时，过C作CB⊥PQ于B，延长BC交x轴于H，如图所示，

则△BPH为等腰直角三角形，BP=BH>BC，
故在线段PQ上必存在A点，使得∠ABC=90°，AB=BC，
将x=2，y=1代入y=－x+b得：b=3，
即b>3；
当直线PQ在C点下方时，过C作CB⊥PQ于B，CB延长线交x轴于H，

则当BQ≥BC时，符合题意，
当直线PQ过H点时，BQ=BC，如图所示，

此时，－1+b=0，即b=1，
即1≤b