初中数学人教版九年级上册24.1.4 圆周角教案配套ppt课件

这是一份初中数学人教版九年级上册24.1.4 圆周角教案配套ppt课件，文件包含2414圆周角pptx、2414圆周角doc等2份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
1.理解圆周角的概念，会叙述并证明圆周角定理.2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.（重点、难点）3.理解掌握圆周角定理的推论及其证明过程和运用.（难点）
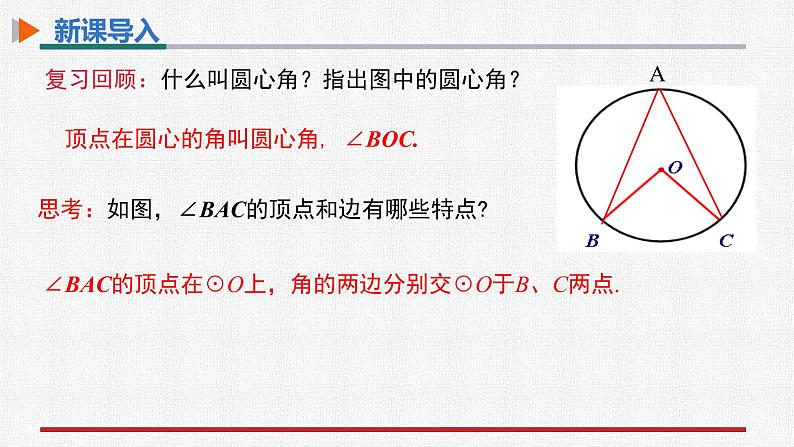
复习回顾：什么叫圆心角？指出图中的圆心角？
顶点在圆心的角叫圆心角, ∠BOC.
思考：如图，∠BAC的顶点和边有哪些特点?
∠BAC的顶点在☉O上，角的两边分别交☉O于B、C两点.
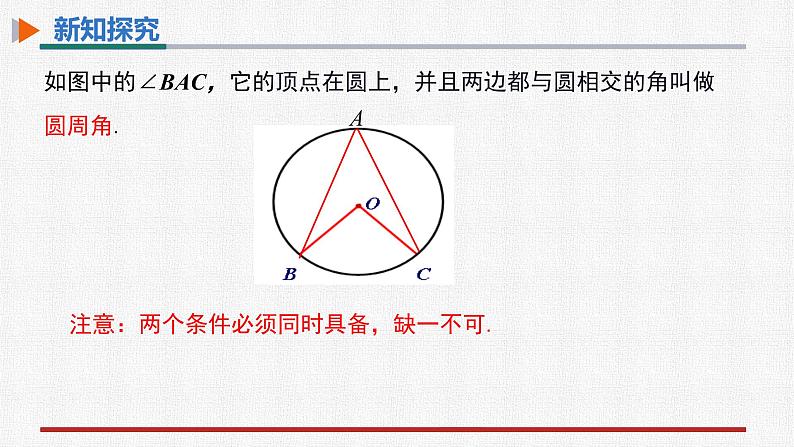
如图中的∠BAC，它的顶点在圆上，并且两边都与圆相交的角叫做圆周角.
注意：两个条件必须同时具备，缺一不可.
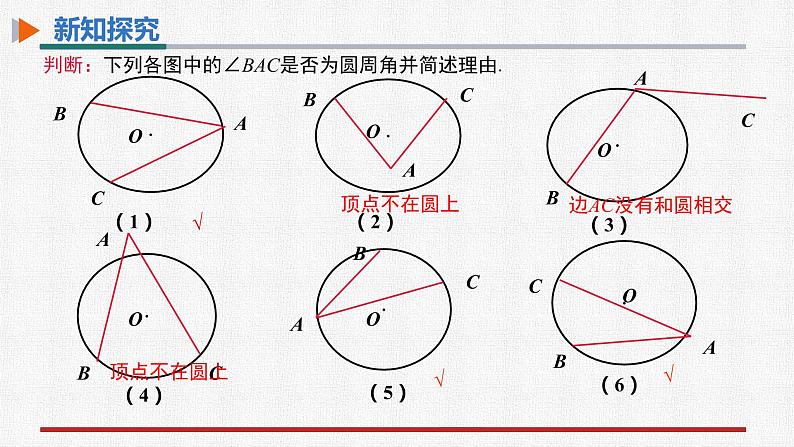
判断：下列各图中的∠BAC是否为圆周角并简述理由.
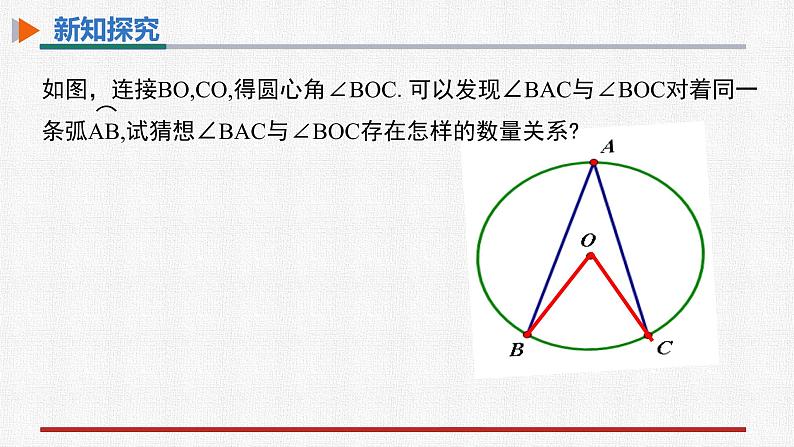
如图，连接BO,CO,得圆心角∠BOC.可以发现∠BAC与∠BOC对着同一条弧AB,试猜想∠BAC与∠BOC存在怎样的数量关系?
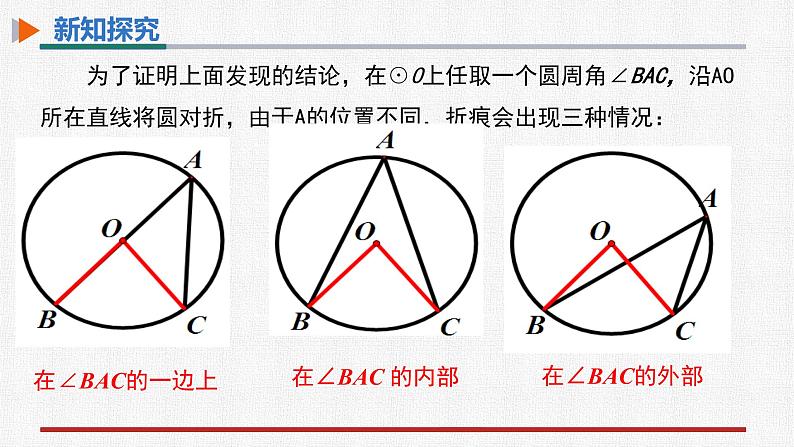
为了证明上面发现的结论，在☉O上任取一个圆周角∠BAC，沿AO所在直线将圆对折，由于A的位置不同，折痕会出现三种情况：
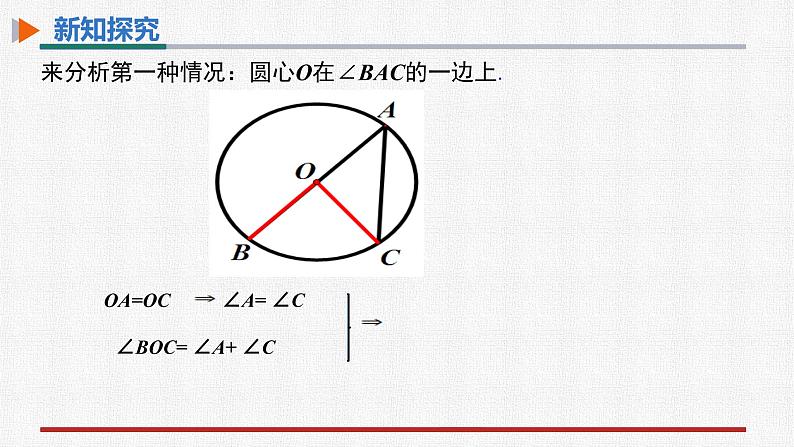
来分析第一种情况：圆心O在∠BAC的一边上.
∠BOC= ∠A+ ∠C
当圆心O在∠BAC的内部时，可以添加辅助线，转化为第一种情况.
当圆心O在∠BAC的外部时，同理可证.
归纳总结：圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.
进一步，还可以得到圆周角定理的推论：
同弧或等弧所对的圆周角相等.
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
请你自己在练习本上完成证明.
例1 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．
∴ ∠ACB= ∠ADB=90°．
又在Rt△ABD中，AD 2+BD 2=AB 2，
例2 如图,AB是⊙O的直径,弦CD交AB于P,∠ACD=60°,∠ADC=70°.求∠APC的度数.
解:连接BC,则∠ACB=90°,
∠DCB＝∠ACB－∠ACD ＝ 90°－60° =30°.
又∵∠BAD=∠DCB=30°,
∴∠APC=∠BAD＋∠ADC＝30°＋70°＝100°.
如果一个多边形所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.
如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关系是什么？
∠A+ ∠C=180º，∠B+ ∠D=180º
思考：如何证明你的猜想呢？
∴∠A＋∠C＝180°，
同理∠B＋∠D＝180°，
圆内接四边形的性质：圆内接四边形的对角互补.
1.顶点在圆上，2.两边都与圆相交
一条弧所对的圆周角等于它所对的圆心角的一半.
（1）同弧或等弧所对的圆周角相等.（2）半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
圆内接四边形的对角互补.
1.如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为(　　)A．30° B．45° C．60° D．75°
2.如图，在⊙O的内接四边形ABCD中，∠BOD＝120°，那么∠BCD的度数是(　　)A．120° B．100°C．80° D．60°
3.在⊙O中，弦AB所对圆心角为40°，则弦AB所对的圆周角为_______________.
4.如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30 °，AB＝2，则⊙O的半径是 .
5.如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
解：设∠A，∠B，∠C的度数分别对于2x，3x，6x，
6. 在圆内接四边形ABCD中， ∠A，∠B，∠C的度数之比是2︰3︰6.求这个四边形各角的度数.
∵四边形ABCD内接于圆，
∴ ∠A+ ∠C=∠B+∠D=180°，
∵2x+6x=180°，
∴ ∠A=45°， ∠B=67.5°， ∠C =135°， ∠D=180°-67.5°=112.5°.
1．如图，CD是⊙O的直径，弦DE∥AO，若∠D的度数为60°，则∠C的度数为（　　）
A．20° B．30° C．40° D．50°
2．如图，点A，B，C均在⊙O上，若∠ACB＝130°，则∠α的度数为（　　）
A．100° B．110° C．120° D．130°
3．如图，四边形ABCD内接于⊙O，连接BD．若 ，∠BDC＝50°，则∠ADC的度数是（　　）
A．125° B．130°C．135° D．140°