北京市第八中学2022-2023学年八年级上学期数学期中试卷(含答案)

2022-2023学年度第一学期期中练习题

一、选择题（每题3分，共24分）在下列各题的四个备选答案中，只有一个是正确的．

1. 下列长度的三条线段能组成三角形的是（    ）

A. 2，3，5 B. 5，6，10 C. 1，1，3 D. 3，4，9

2. 下列因式分解正确的是（    ）

A.  B.

C.  D.

3. 如图，两个三角形全等，则等于（    ）

A.  B.  C.  D.

4. 已知是完全平方式，则m的值是（    ）

A. 1 B. 2 C.  D.

5. 如图，在中，点D是边BC的中点，，的面积是4，则下列结论正确的是（    ）

A.  B.  C.  D.

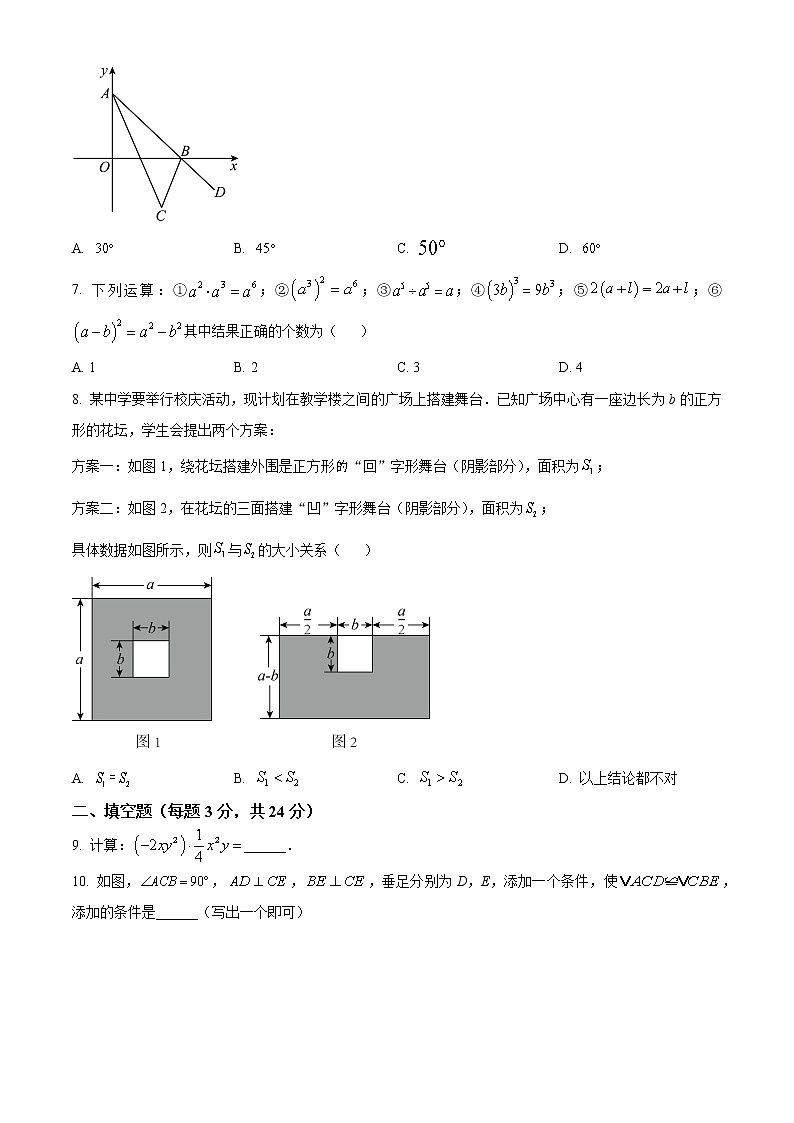
6. 如图，若点A在y轴上，点B在x轴上， 平分线交外角的平分线于点C，则的度数是（    ）

A.  B.  C.  D.

7. 下列运算：①；②；③；④；⑤；⑥其中结果正确的个数为（    ）

A. 1 B. 2 C. 3 D. 4

8. 某中学要举行校庆活动，现计划在教学楼之间的广场上搭建舞台．已知广场中心有一座边长为b的正方形的花坛，学生会提出两个方案：

方案一：如图1，绕花坛搭建外围是正方形“回”字形舞台（阴影部分），面积为；

方案二：如图2，在花坛的三面搭建“凹”字形舞台（阴影部分），面积为；

具体数据如图所示，则与的大小关系（    ）

A.  B.  C.  D. 以上结论都不对

二、填空题（每题3分，共24分）

9. 计算：______．

10. 如图，，，，垂足分别为D，E，添加一个条件，使，添加的条件是______（写出一个即可）

11 若，，则______；______．

12. 如图，，且，则______度．

13. 若多项式能因式分解，则正整数k的值等于______．

14. 如图，在中，是的角平分线，在射线上，于，，，则______度．

15. 已知：一个周长为10的等腰三角形，设底边长为x，腰长为y，则x与y的数量关系是______，若这个等腰三角形的三边均为整数，则这样的三角形有______个．

16. 如图，点D是等边边上的一个动点，以为边作等边，连接．则下列结论正确的是______（填正确的序号）．

①；②D在上运动的过程中线段有最小值；③四边形的面积是定值；④．

三、解答题（17题6分，18题7分，19题4分，20题11分，21题5分，22题5分，23题7分，24题7分，共52分）

17. 按下列要求画图并回答问题：

（1）在图1中将的面积分成1：3的两部分，并描述你的作法______________；

（2）在图2中，完成以下问题：

①作高，；

②比较______的大小（用“>”“<”“=”填空）；

③请用无刻度的直尺（只能画直线）作出边上的高，描述的作法_____．

18. 计算：

（1）；

（2）

19. 图，，，．求证：．

20. 分解因式：

（1）；

（2）；

（3）．

21. 先化简，再求值：，其中．

22. 如图，在中，BE平分，．

（1）求证：；

（2）若，证明：

23. 探究与发现：我们在过去的学习中已经发现了如下的运算规律：

，

，

，

……

（1）设a为整数，且，请用含a的等式写出一般的规律______；

（2）小戴同学通过计算下列两位数的乘积，发现结果也存在一定的规律，请你补充小戴同学的探究过程：

，，，……

①观察相乘的两位数，可以发现，两位数的十位上的数字______，个位上的数字的和等于______；

②根据发现，若设一个两位数的十位上的数字为m，个位上的数字为n，则另一个两位数的个位上的数字为______（其中m，n为小于10的正整数）．则以上两位数相乘的规律是______（用含m、n的等式表示）；

③利用发现的规律计算： ______；

④请用所学知识证明②中的规律．

24. 如图，是的平分线，E是上的一点，作交直线于点P（点P与B，C，D不重合）．

（1）当E是的中点时，求证：；

（2）当点E在上移动时，补全图形，直接写出与的数量关系：______．

附加卷

25. 如图，在四边形中，D，E分别是边，上的动点，将四边形沿折叠，

（1）如图1，，与，数量关系是______，

（2）如图2，，与，的数量关系是______．

26. 爱思考的小郭同学发现教科书中介绍了多项式除以单项式的方法，并没有介绍多项式除以多项式的方法，通过查阅资料小郭同学发现了多项式除以多项式的一种方法叫“综合除法”，综合除法主要用于一元多项式，除以一次多项式的演算，以便获得商式和余式，具体方法如下：

①写出分离系数竖式：

②进行相关计算：

将落下得到，计算并置于下方，计算得到；计算并置于下方，计算得到……计算并置于下方，计算得到．

③写出计算结果：除以得到商式

和余式．

解决问题：利用综合除法求除以的商式和余式．

由此可知，除以的商式是______，余式是______．

2022-2023学年度第一学期期中练习题

一、选择题（每题3分，共24分）在下列各题的四个备选答案中，只有一个是正确的．

【1题答案】

【答案】B

【2题答案】

【答案】A

【3题答案】

【答案】C

【4题答案】

【答案】D

【5题答案】

【答案】D

【6题答案】

【答案】B

【7题答案】

【答案】A

【8题答案】

【答案】C

二、填空题（每题3分，共24分）

【9题答案】

【答案】

【10题答案】

【答案】（答案不唯一）

【11题答案】

【答案】    ①. 8    ②. 12

【12题答案】

【答案】50

【13题答案】

【答案】9

【14题答案】

【答案】

【15题答案】

【答案】    ①.     ②.

【16题答案】

【答案】①②③④

三、解答题（17题6分，18题7分，19题4分，20题11分，21题5分，22题5分，23题7分，24题7分，共52分）

【17题答案】

【答案】（1）作图见解析，作法：找到线段的四等分点E，连接；   

（2）①作图见解析；②；③见解析，延长，交于点O，连接并延长，交于点F，则为边上的高．

【18题答案】

【答案】（1）   

（2）

【19题答案】

【答案】见解析

【20题答案】

【答案】（1）   

（2）   

（3）

【21题答案】

【答案】，25

【22题答案】

【答案】（1）见解析；   

（2）见解析．

【23题答案】

【答案】（1）   

（2）①相同，；②，；③；④见解析

【24题答案】

【答案】（1）见解析；   

（2）图形见解析，或．

附加卷

【25题答案】

【答案】（1）   

（2）

【26题答案】

【答案】    ①. ；    ②. 2．