2022-2023学年贵州省贵阳市云岩区为明学校八年级（上）第一次月考数学试卷-（含解析）

2022-2023学年贵州省贵阳市云岩区为明学校八年级（上）第一次月考数学试卷

一、选择题（本题共12小题，共36分）

1.    下列式子一定是二次根式的是(    )

A.  B.  C.  D.

2.    实数，，，中，无理数是(    )

A.  B.  C.  D.

3.    若二次根式有意义，则的取值范围是(    )

A.  B.  C.  D.

4.    下列四组数中，属于勾股数的是(    )

A. ，， B. ，， C. ，， D. ，，

5.    如图，在中，，，则的值是(    )

A.
B.
C.
D.

6.    若一正数的两个平方根分别为和，则的值是(    )

A.  B.  C.  D.

7.    若，则的值为(    )

A.  B.  C.  D.

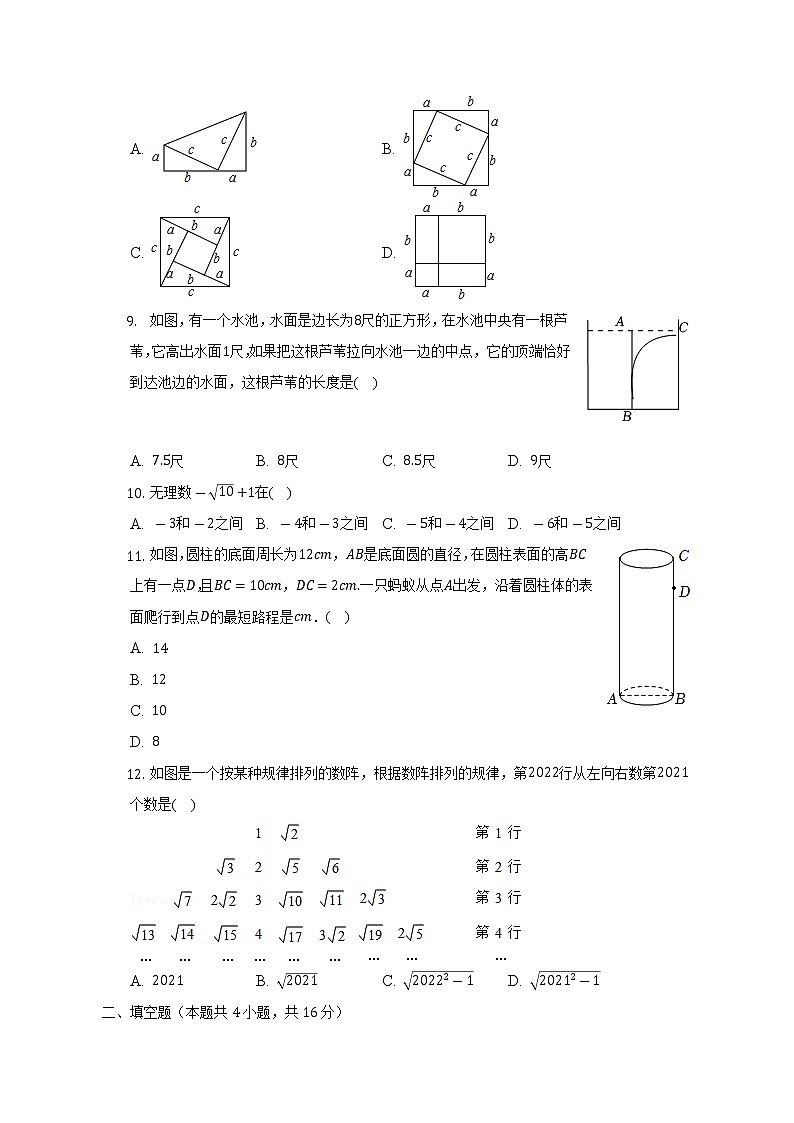
8.    勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中不能证明勾股定理的是(    )

A.  B.
C.  D.

9.    如图，有一个水池，水面是边长为尺的正方形，在水池中央有一根芦苇，它高出水面尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，这根芦苇的长度是(    )

A. 尺 B. 尺 C. 尺 D. 尺

10. 无理数在(    )

A. 和之间 B. 和之间 C. 和之间 D. 和之间

11. 如图，圆柱的底面周长为，是底面圆的直径，在圆柱表面的高上有一点，且，一只蚂蚁从点出发，沿着圆柱体的表面爬行到点的最短路程是．(    )

A.
B.
C.
D.

12. 如图是一个按某种规律排列的数阵，根据数阵排列的规律，第行从左向右数第个数是(    )
     

A.  B.  C.  D.

二、填空题（本题共4小题，共16分）

13. 把化为最简二次根式得______．
14. 利用计算器，得，，，，按此规律，可得
    的值约为______．
15. 若最简二次根式与最简二次根式是同类二次根式，则______．
16. 如图，在中，，，，分别以的三边为直径画半圆，则两个月形图案阴影部分的面积之和是______．

三、解答题（本题共9小题，共98分）

17. 计算：
    ；
    ．
18. 把下列各数填入相应的集合里：，，，，，，．
    正数集合：______；
    负数集合：______；
    有理数集合：______；
    无理数集合：______．
19. 已知，，分别求下列代数式的值：
    ；
    ．
20. 如图，明明在距离水面高度为的岸边处，用绳子拉船靠岸，开始时绳子的长为若明明收绳后，船到达处，则船向岸移动了多少米？

21. 已知、互为相反数，、互为倒数，的倒数等于它本身，求的立方根．
22. 如图，是边长为的正方形的对角线，以点为圆心，长为半径画弧，在点右侧交数轴于点，则点表示的数是______；
    请仿照的作法，在图的数轴上描出表示数的点．
     
23. 某运动公园有一块空地，如图，四边形所示，公园管理处计划在四边形区域内种植草坪，绿化环境，并在处修一条小路，经测量：已知，米，米，米，米．
    求小路的长；
    判断的形状，并求出种植草坪的面积．

24. 小红家最近新盖了房子，室内装修时，木工师傅让小红爸爸去建材市场买一块长，宽的薄木板用来做家居面，到了市场爸爸看到满足这个尺寸的木板有点大，买还是不买爸爸犹豫了，因为他知道他家门框高只有，宽只有，他不知道这块木板买回家后能不能完整的通过自家门框．请你替小红爸爸解决一下难题，帮他算一算要买的木板能否通过自家门框进入室内．备用图可供做题参考，薄木板厚度可以忽略不计
25. 在数学课外学习活动中，嘉琪遇到一道题：已知，求的值．她是这样解答的：
    解：，
    ，
    ，即，
    ，
    ．
    请你根据嘉琪的解题过程，解决如下问题：
    化简：______，______；
    化简；
    若，求的值．
    

答案和解析

1.【答案】 

【解析】解：、当时，二次根式无意义，故选项A一定是二次根式，选项A不符合题意；
B、是二次根式，故选项B符合题意；
C、当时，此时二次根式无意义，故选项C不一定是二次根式，选项C不符合题意；
D、，二次根式无意义，故选项D一定不是二次根式，选项D不符合题意；
故选：．
根据二次根式的定义判断即可．
本题考查二次根式的定义，掌握二次根式的定义：一般地，我们把形如的式子叫做二次根式是解题的关键．
 

2.【答案】 

【解析】解：、是无理数，故本选项符合题意；
B、是分数，属于有理数，故本选项不合题意；
C、是整数，属于有理数，故本选项不合题意；
D、是整数，属于有理数，故本选项不合题意；
故选：．
根据无理数的定义求解即可．
此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如，，每两个之间依次多个等形式．
 

3.【答案】 

【解析】解：由题意得：，
解得：，
故选：．
根据二次根式有意义的条件可得，再解即可．
此题主要考查了二次根式有意义，关键是掌握二次根式中的被开方数是非负数．
 

4.【答案】 

【解析】解：、，，不是正整数，，，不是勾股数；
B、，，，是勾股数；
C、，，，不是勾股数；
D、，不是正整数，，，不是勾股数；
故选：．
利用勾股数的定义进行分析即可．
此题主要考查了勾股数，关键是掌握勾股数的定义：满足的三个正整数，称为勾股数．
 

5.【答案】 

【解析】解：由勾股定理得：，
即，
故选：．
由勾股定理可直接得出结果．
本题考查了勾股定理，熟练掌握勾股定理是解题的关键．
 

6.【答案】 

【解析】解：一正数的两个平方根分别为和，
，
解得：，
则，
，
故选：．
根据一个正数的两个平方根互为相反数建立方程，解方程求出的值，由此即可得．
本题考查了平方根的性质和一元一次方程的应用，熟练掌握平方根的性质一个正数的两个平方根互为相反数是解题关键．
 

7.【答案】 

【解析】解：由题意可知：，，
，，
，
故选：．
根据非负数的性质即可求出与的值，然后代入原式即可求出答案．
本题考查平方根与立方根，解题的关键是熟练运用平方根与立方根的定义，本题属于基础题型．
 

8.【答案】 

【解析】解：在选项中，由图可知三个三角形的面积的和等于梯形的面积，
，
整理可得，
选项可以证明勾股定理，
在选项中，大正方形的面积等于四个三角形的面积加小正方形的面积，
，
整理得，
选项可以证明勾股定理，
在选项中，大正方形的面积等于四个三角形的面积加小正方形的面积，
，
整理得，
选项可以说明勾股定理，
在选项中，大正方形的面积等于四个矩形的面积的和，
，
以上公式为完全平方公式，
选项不能说明勾股定理，
故选：．
勾股定理有两条直角边，一条斜边，共三个量，根据勾股定理的概念即可判断．
本题主要考查勾股定理的证明过程，关键是要牢记勾股定理的概念，在直角三角形中，两条直角边的平方和等于斜边的平方．
 

9.【答案】 

【解析】解：设芦苇的长度为尺，则为尺，
根据勾股定理得：，
解得：，
芦苇的长度尺，
故选：．
找到题中的直角三角形，设芦苇的长度为尺，根据勾股定理解答．
本题考查了勾股定理的应用，善于观察题目的信息是解题以及学好数学的关键．
 

10.【答案】 

【解析】解：，即，
，
，
即，
故选：．
估算无理数的大小，进而得出的大小即可．
本题考查估算无理数的大小，掌握算术平方根的定义以及不等式的性质是正确解答的关键．
 

11.【答案】 

【解析】解：圆柱侧面展开图如图所示，

圆柱的底面周长为，
．
，
在中，，
，
即蚂蚁从点出发沿着圆柱体的表面爬行到点的最短距离是．
故选：．
首先画出圆柱的侧面展开图，根据底面周长为，求出的值；再在中，根据勾股定理求出的长，即为所求．
此题主要考查了平面展开图，以及勾股定理的应用，做题的关键是画出圆柱的侧面展开图．
 

12.【答案】 

【解析】解：第行，第个数是，即，
第行，第个数是，即，
第行，第个数是，即，

第行，第个数是，即，
所以第行，第个数是，
故选：．
根据数阵的排列规律可得答案．
本题考查二次根式的性质与化简，数字的变化类，发现数阵的排列规律是正确解答的前提．
 

13.【答案】 

【解析】解：，
故答案为：．
利用二次根式的性质和最简二次根式的定义解答即可．
本题主要考查了二次根式的性质和最简二次根式的定义，正确利用二次根式的性质进行化简是解题的关键．
 

14.【答案】 

【解析】解：由题意知，被开方数每扩大为原来的倍，其算术平方根相应的扩大为原来的倍，
，
，
故答案为：．
由已知数据得出被开方数每扩大为原来的倍，其算术平方根相应的扩大为原来的倍，据此求解可得．
本题主要考查计算器数的开方，解题的关键是得出被开方数每扩大为原来的倍，其算术平方根相应的扩大为原来的倍的规律．
 

15.【答案】 

【解析】解：最简二次根式与最简二次根式是同类二次根式，
，
解得：．
故答案为：．
根据同类二次根式的被开方数相同可得出关于的方程，解出即可．
本题考查了同类二次根式的知识，注意掌握同类二次根式化为最简二次根式后被开方数相同且根指数均为．
 

16.【答案】 

【解析】解：，
，，
设以、、为直径的半圆分别为、、，
，
同理：，，
，
，
即两个月形图案阴影部分的面积之和是，
故答案为：．
由勾股定理得，，设以、、为直径的半圆分别为、、，则，而，即可解决问题．
本题考查了勾股定理以及半圆面积的计算等知识，将阴影部分的面积转化为的面积是解题的关键．
 

17.【答案】解：原式

；

原式
． 

【解析】直接化简二次根式，进而合并同类二次根式得出答案；
直接利用完全平方公式以及二次根式的乘法运算法则、零指数幂的性质分别化简，进而得出答案．
此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．
 

18.【答案】，，  ，，，  ，，，，，   

【解析】解：正数集合：；
负数集合：；
有理数集合：；
无理数集合：；
故答案为：，，；，，；，，，，，；．
根据实数的分类进行计算即可．
本题考查了实数的分类，掌握实数的分类是解题的关键．
 

19.【答案】解：，，
，，
；
． 

【解析】根据二次根式的加法法则、减法法则分别求出，，再根据平方差公式计算；
根据完全平方公式计算．
本题考查的是二次根式的化简求值，掌握完全平方公式、平方差公式是解题的关键．
 

20.【答案】解：开始时绳子的长为明明收绳后，船到达处，
，
由题意得：，，
，
，
，
船向岸移动了米，
答：船向岸移动了米． 

【解析】先求出，再由勾股定理求出、，即可得出答案．
本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．
 

21.【答案】解：、互为相反数，
，
、互为倒数，
，
的倒数等于它本身，
，
当；；时，
，
的立方根为；
当；；时，
，
的立方根为．
综上所述，的立方根是或． 

【解析】根据题意得，，，以整体的形式代入所求的代数式即可．
本题考查的是相反数、倒数和一个数的立方根的问题，又考查了代数式求值的方法，同时还隐含了整体的数学思想和正确运算的能力．
 

22.【答案】 

【解析】解：由作法得，
，
，
点表示的数为；
故答案为：；
如图，点为所作．

先利用勾股定理计算出，再利用作法得到，然后根据数轴表示数的方法得到点表示的数；
如图，是长、宽分别为、的长方形的对角线，以点为圆心，长为半径画弧，在点右侧交数轴于点，则点表示的数为．
本题考查了作图复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了实数与数轴．
 

23.【答案】解：在直角中，，米，米，则：
米．
答：小路的长为米；
在中，米，米，米，则：
米，米
所以．
所以是直角三角形，且．
故米
答：是直角三角形，种植草坪的面积是米． 

【解析】在直角中，利用勾股定理求小路的长；
由勾股定理逆定理判断的形状，由三角形面积公式求得种植草坪的面积．
本题考查勾股定理的应用，四边形的面积等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
 

24.【答案】解：连接，如图所示：
，，
在中，根据勾股定理：
，
，
，
小红爸爸要买的木板能通过自家门框进入室内． 

【解析】本题考查了勾股定理的应用，熟练掌握勾股定理是解决问题的关键．
连接，由勾股定理解得，由，得出，即可得出结果．
 

25.【答案】  

【解析】解：

，


，
故答案为：，；


；


，
，
，即，




．
根据分母有理化的方法进行求解即可；
把各项进行分母有理化，从而可求解；
仿照所给的解答方式进行求解．
本题主要考查二次根式的化简求值，分母有理化，解答的关键是对相应的运算法则的掌握．