

华师大版八年级上册3 角平分线评课ppt课件
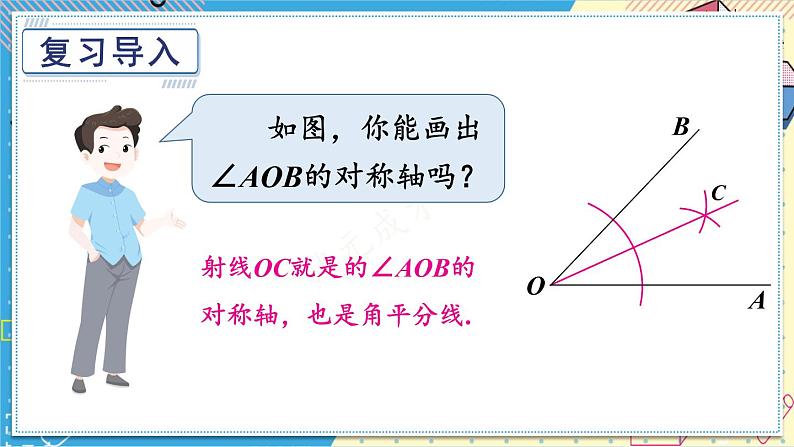
展开如图,你能画出∠AOB的对称轴吗?
射线OC就是的∠AOB的对称轴,也是角平分线.
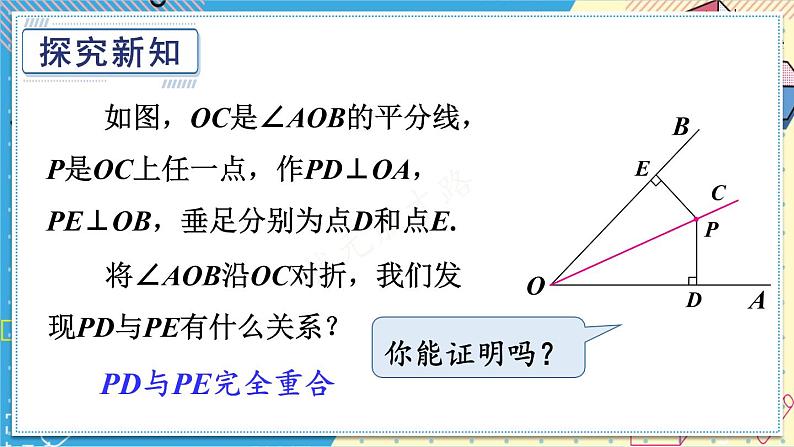
如图,OC是∠AOB的平分线,P是OC上任一点,作PD⊥OA,PE⊥OB,垂足分别为点D和点E.
将∠AOB沿OC对折,我们发现PD与PE有什么关系?
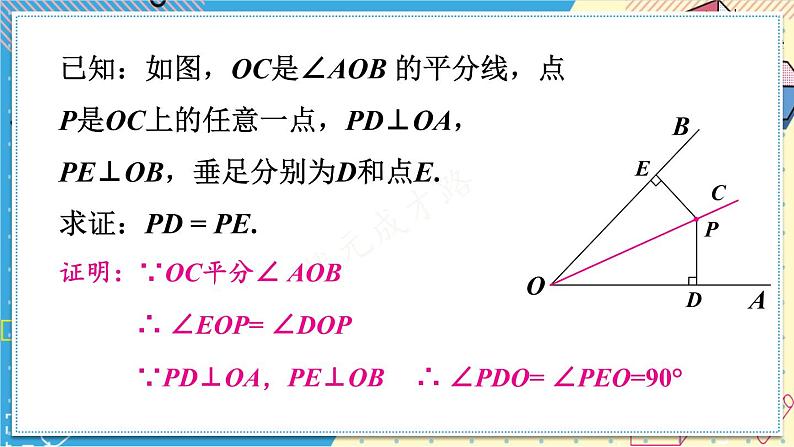
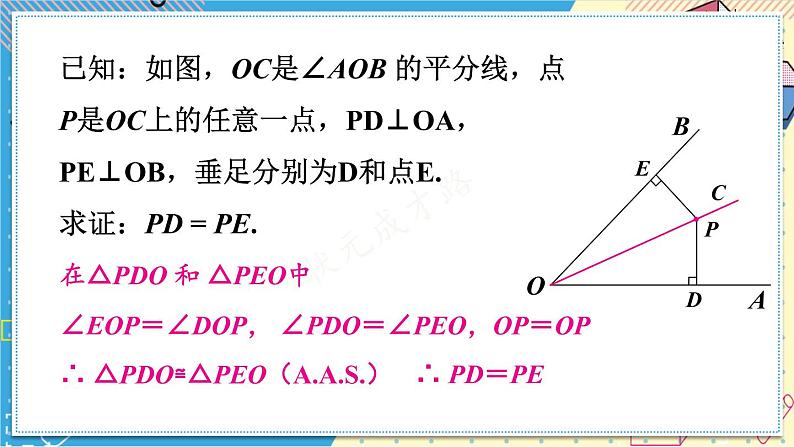
已知:如图,OC是∠AOB 的平分线,点P是OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为D和点E.求证:PD = PE.
证明:∵OC平分∠ AOB
∴ ∠EOP= ∠DOP
∵PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO=90°
在△PDO 和 △PEO中
∠EOP=∠DOP, ∠PDO=∠PEO,OP=OP
∴ △PDO≌△PEO()
角平分线上的点到角两边的距离相等.
∵ ∠1= ∠2, PD⊥OA, PE⊥OB
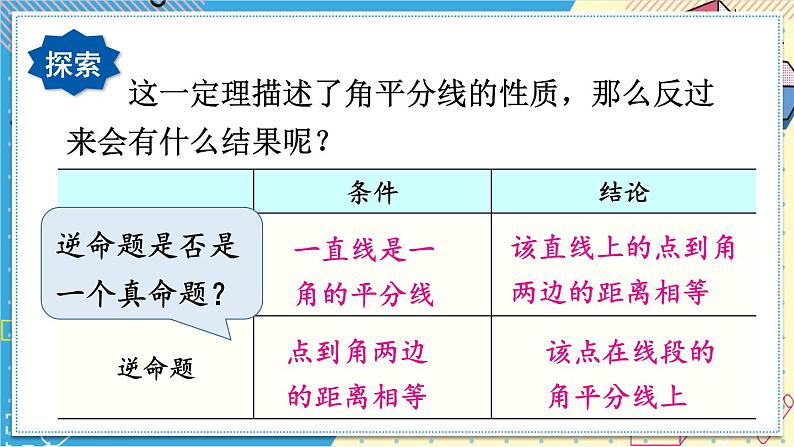
这一定理描述了角平分线的性质,那么反过来会有什么结果呢?
该直线上的点到角两边的距离相等
该点在线段的角平分线上
逆命题是否是一个真命题?
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE. 求证:点Q在∠AOB的平分线上.
证明:过点O、Q作射线OQ.
∵OQ⊥OA,QE⊥OB,
∴∠QDO=∠QEO=90°
在Rt△QDO和Rt△QEO中,
∵OQ=OQ,QD=QE,
∴Rt△QDO≌Rt△QEO(H.L.)
∴点Q在∠AOB的平分线上.
角的内部到角两边距离相等的点在角的平分线上.
角平分线的性质定理与判定定理互为逆定理
如何证明“三角形三条边的角平分线交于一点”?
只需证明其中两条角平分线的交点一定在第三条角平分线上就可以了.
AO是∠BAC的平分线
BO是∠ABC的平分线
试试看,现在你会证明了吗?
1. 如图,在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.
提示:作∠AOB的平分线OP,它与l的交点P,即为所求的点.
2.如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F. 求证:点F在∠DAE的平分线上.
证明:作FG⊥AC,FH⊥BC,FM⊥AB﹐垂足分别为G、H 、M .
∵ CF平分∠ECB,BF平分∠CBD
∴ FG=FH=FM
∴点F在∠DAE的平分线上.
华师大版八年级上册3 角平分线课文配套课件ppt: 这是一份华师大版八年级上册3 角平分线课文配套课件ppt,共22页。PPT课件主要包含了备选习题等内容,欢迎下载使用。
八年级上册3 角平分线说课课件ppt: 这是一份八年级上册3 角平分线说课课件ppt,文件包含3角平分线pptx、3角平分线doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
华师大版八年级上册3 角平分线评课课件ppt: 这是一份华师大版八年级上册3 角平分线评课课件ppt,共38页。PPT课件主要包含了学习目标,本节要点,学习流程,知识点,角平分线的性质定理,感悟新知,角平分线的判定定理,本节小结,角平分线,三角形的角平分线等内容,欢迎下载使用。













