华师大版八年级上册3 角平分线教学设计

 角平分线的性质

教学目标 ：1． 掌握角的平分线的性质定理和它的逆定理的内容、证明及应用。

2． 理解原命题和逆命题的概念和关系，会找一个简单命题的逆命题．

3． 渗透角平分线是满足特定条件的点的集合的思想。

教学重点和难点 ：角平分线的性质定理和逆定理的应用是重点． 性质定理和判定定理的区别和灵活运用是难点．

如图，AB＝AD，BC＝DC，　沿着AC画一条射线AE，AE就是∠BAD的角平分线，　你知道为什么吗？

用直尺和圆规作角的平分线

已知：∠AOB

求作：射线OC

使∠AOC =∠BOC

做法：

探究角平分线的性质

(1)实验：将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开，观察两次折叠形成的三条折痕，你能得出什么结论？

(2)猜想:角的平分线上的点到角的两边的距离相等.

已知：如图，OC平分∠AOB，点P在OC上，PD⊥OA于点D，PE⊥OB于点E

求证:   PD=PE

几何书写

在Rt△ABC中，BD平分∠ABC，DE⊥AB于E，则：

⑴图中相等的线段有哪些？相等的角呢？

⑵哪条线段与DE相等？为什么？

⑶若AB＝10，BC＝8，AC＝6，　　　　　　求BE，AE的长和△AED的周长。

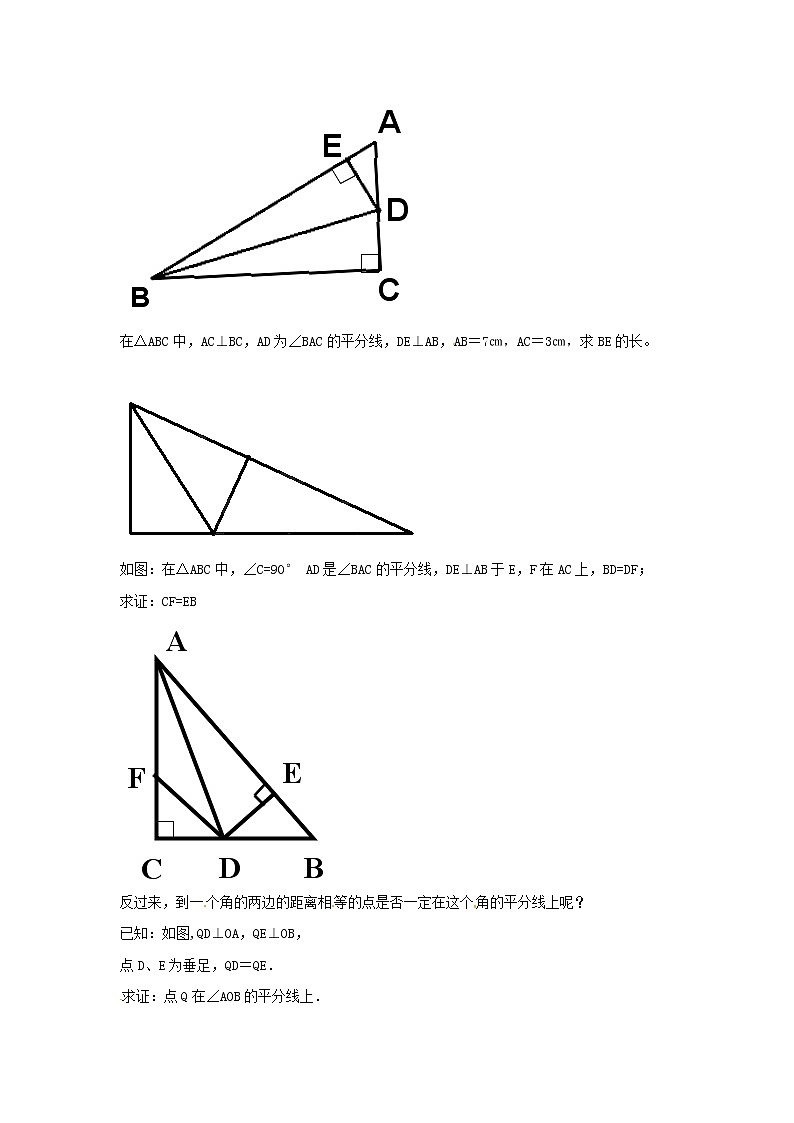
在△ABC中，AC⊥BC，AD为∠BAC的平分线，DE⊥AB，AB＝7㎝，AC＝3㎝，求BE的长。

如图：在△ABC中，∠C=90° AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF；          求证：CF=EB

反过来，到一个角的两边的距离相等的点是否一定在这个角的平分线上呢？

已知：如图,QD⊥OA，QE⊥OB，

点D、E为垂足，QD＝QE．

求证：点Q在∠AOB的平分线上．

2.到角的两边的距离相等的点在角的平分线上。

用数学语言表示为：

∵ QD⊥OA，QE⊥OB，QD＝QE．

∴点Q在∠AOB的平分线上．

角的平分线上的点到角的两边的距离相等.

∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上

∴ QD＝QE

思考：

要在Ｓ区建一个集贸市场，使它到公路，铁路距离相等且离公路，铁路的交叉处５００米，应建在何处？（比例尺 1：20 000）

例  已知：如图，△ABC的角平分线BM、CN相交于点P.
求证：点P到三边AB、BC、CA的距离相等.

练习：如图，△ＡＢＣ的∠Ｂ的外角的平分线ＢＤ与∠Ｃ的外角的平分线ＣＥ相交于点Ｐ．求证：点Ｐ到三边ＡＢ，ＢＣ，ＣＡ所在直线的距离相等．

如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，且BE＝CF。
求证：AD是△ABC的角平分线。