辽宁省大连市沙河口区格致中学2022—2023学年上学期八年级月考数学试卷（含答案）

2022-2023学年格致中学秋季八年级数学月考试卷+解析

一、选择题（本题共10小题，每小题2分，共20分，在每小题给出的四个选项中，只有一个选项正确)

1、下面三个边中，能组成三角形的是（    ）

A、4cm  6cm    8cm           B、1cm   2cm  4cm   

C、5cm  6cm    12cm          D、2cm  3cm  5cm

2、下列计算正确的是（    ）

A、a²·a³=   B、a²+2a²=2   C、（a²）³=    D、(ab）²=a²b²

3、下列四个图形中，线段AD是△ABC中BC边上的高的是（    ）

A、             B、           C、                  D、

4、如图，已知△ABC的三条边和三个角，则甲、乙、丙三个三角形中和△ABC全等的是（  ）

A、甲和乙      B、甲和丙         C、乙和丙       D、只有甲

5、下列能用平方差公式计算的是（    ）

A、（-x+y）（x+y）B、（-x+y）（x-y）C、（x+2）（2+x）D、（2x+3）（3x-2）

6、若等腰三角形的两边长分别为3cm和8cm，则它的周长为（    ）

A、14cm    B、14cm或19cm    C、19cm    D、以上都不对

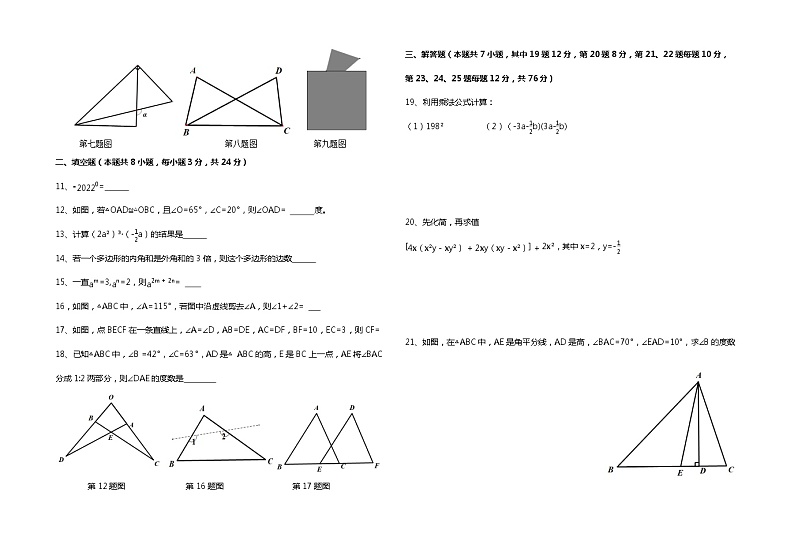
7、一副三角尺如图摆放，则α的大小为（    ）

A、105°        B、120°        C、135°       D、150°

8、如图，在△ABC和△DCB中，一直∠ACB=∠DBC，则添加以下条件，仍不能判定△ABC≌△DCB的是（    ）

A、∠ABC=∠DCB  B、AB=DC   C、AC=DB   D、∠A=∠D

9、如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（  ）

A、SSS  B、SAS     C、AAS     D、ASA

10如果a=，c=，那么（    ）

A、a＞b＞c      B、b＞c＞a       C、c＞a＞b     D、c＞b＞a

  第七题图                            第八题图              第九题图

二、填空题（本题共8小题，每小题3分，共24分）

11、-=       

12、如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=       度。

13、计算（2a²）³·（-a）的结果是       

14、若一个多边形的内角和是外角和的3倍，则这个多边形的边数     

15、一直=3,=2，则=      

16，如图，△ABC中，∠A=115°，若图中沿虚线剪去∠A，则∠1+∠2=   

17、如图，点BECF在一条直线上，∠A=∠D，AB=DE，AC=DF，BF=10，EC=3，则CF=

18、已知△ABC中，∠B =42°，∠C=63°，AD是△ ABC的高，E是BC上一点，AE将∠BAC分成1:2两部分，则∠DAE的度数是         

第12题图               第16题图                 第17题图    

三、解答题（本题共7小题，其中19题12分，第20题8分，第21、22题每题10分，第23、24、25题每题12分，共76分）

19、利用乘法公式计算：

（1）198²          （2）（-3a-b)(3a-b)

20、先化简，再求值

2x²，其中x=2，y=-

21、如图，在△ABC中，AE是角平分线，AD是高，∠BAC=70°，∠EAD=10°，求∠B的度数

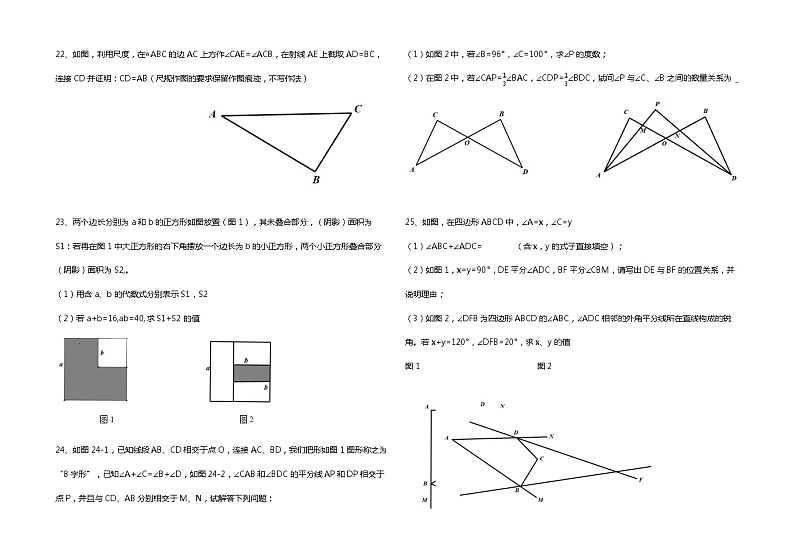
22、如图，利用尺度，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD并证明：CD=AB（尺规作图的要求保留作图痕迹，不写作法）

23、两个边长分别为a和b的正方形如图放置（图1），其未叠合部分，（阴影）面积为S1：若再在图1中大正方形的右下角摆放一个边长为b的小正方形，两个小正方形叠合部分（阴影）面积为S2,。

（1）用含a、b的代数式分别表示S1，S2

（2）若a+b=16,ab=40,求S1+S2的值

           图1                               图2

24、如图24-1，已知线段AB、CD相交于点O，连接AC、BD，我们把形如图1图形称之为“8字形”，已知∠A+∠C=∠B+∠D，如图24-2，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N，试解答下列问题：

（1）如图2中，若∠B=96°，∠C=100°，求∠P的度数；

（2）在图2中，若∠CAP=∠BAC，∠CDP=∠BDC，试问∠P与∠C、∠B之间的数量关系为             

25、如图，在四边形ABCD中，∠A=x，∠C=y

（1）∠ABC+∠ADC=        （含x，y的式子直接填空）；

（2）如图1，x=y=90°，DE平分∠ADC，BF平分∠CBM，请写出DE与BF的位置关系，并说明理由；

（3）如图2，∠DFB为四边形ABCD的∠ABC，∠ADC相邻的外角平分线所在直线构成的锐角。若x+y=120°，∠DFB=20°，求x、y的值

图1                             图2

2022-2023学年格致中学秋季八年级数学月考试卷+解析

一、选择题（本题共10小题，每小题2分，共20分，在每小题给出的四个选项中，只有一个选项正确)

1、下面三个边中，能组成三角形的是（    ）

A、4cm  6cm    8cm           B、1cm   2cm  4cm   

C、5cm  6cm    12cm          D、2cm  3cm  5cm

答案：A

4、下列计算正确的是（    ）

B、a²·a³=   B、a²+2a²=2   C、（a²）³=    D、(ab）²=a²b²

    答案：D

5、下列四个图形中，线段AD是△ABC中BC边上的高的是（    ）

B、             B、           C、                  D、

    答案：D

4、如图，已知△ABC的三条边和三个角，则甲、乙、丙三个三角形中和△ABC全等的是（  ）

A、甲和乙      B、甲和丙         C、乙和丙       D、只有甲

    答案：A

5、下列能用平方差公式计算的是（    ）

B、（-x+y）（x+y）B、（-x+y）（x-y）C、（x+2）（2+x）D、（2x+3）（3x-2）

    答案：A

7、若等腰三角形的两边长分别为3cm和8cm，则它的周长为（    ）

A、14cm    B、14cm或19cm    C、19cm    D、以上都不对

答案：C

7、一副三角尺如图摆放，则α的大小为（    ）

A、105°          B、120°          C、135°     D、150°

答案：A

8、如图，在△ABC和△DCB中，一直∠ACB=∠DBC，则添加以下条件，仍不能判定△ABC≌△DCB的是（    ）

A、∠ABC=∠DCB      B、AB=DC     C、AC=DB     D、∠A=∠D

答案：B

9、如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（  ）

A、SSS  B、SAS     C、AAS     D、ASA

答案：B

10如果a=，c=，那么（    ）

B、a＞b＞c      B、b＞c＞a       C、c＞a＞b     D、c＞b＞a

    答案：B

  第七题图                            第八题图              第九题图

二、填空题（本题共8小题，每小题3分，共24分）

11、-=       

答案：-1

12、如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=       度。

答案：95°

13、计算（2a²）³·（-a）的结果是       

答案：-

14、若一个多边形的内角和是外角和的3倍，则这个多边形的边数     

答案：8

15、一直=3,=2，则=      

答案：36

16，如图，△ABC中，∠A=115°，若图中沿虚线剪去∠A，则∠1+∠2=   

答案：295°

17、如图，点B、E、C、F在一条直线上，∠A=∠D，AB=DE，AC=DF，BF=10，EC=3，则CF=

答案：3.5

18、已知△ABC中，∠B =42°，∠C=63°，AD是△ ABC的高，E是BC上一点，AE将∠BAC分成1:2两部分，则∠DAE的度数是         

答案：23°

第12题图               第16题图                 第17题图    

三、解答题（本题共7小题，其中19题12分，第20题8分，第21、22题每题10分，第23、24、25题每题12分，共76分）

19、利用乘法公式计算：

（1）198²          （2）（-3a-b)(3a-b)

答案：

（1）198²=（100-2）²=100²-2×100×2-2²=10000-400-4=9596

（2）（-3a-b)(3a-b)

     =（-b）²-（3a）²=b²-9a²

20、先化简，再求值

2x²，其中x=2，y=-

答案：2x²

     =（4x³y-4x²y²+2x²y²-2x³y）+2x²

     =（2x³y-2x²y²）+2x²

     =2x²+2x³y-2x²y²

当x=2，y=-时

2x²+2x³y-2x²y²

=-2

21、如图，在△ABC中，AE是角平分线，AD是高，∠BAC=70°，∠EAD=10°，求∠B的度数

解：∵∠BAC=70°，AE是角分线，

∴∠BAE=∠EAC=35°

在△DEA中，∵AD⊥BC，∴∠ADE=90°，∠DAD=10°

 ∴∠AED=80°

∵∠AED=∠BAE+∠B

∴∠B=∠AED-∠BAE=80°-35°=55°

22、如图，利用尺度，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD并证明：CD=AB（尺规作图的要求保留作图痕迹，不写作法）

【分析】先按照题意作图，然后证明△ADC≌△CBA即可得到AB=CD，

【详解】解：如图所示，即为所求；

∵∠CAE=∠ACB，AC=CA，AD=CB，

∴△ADC≌△CBA（SAS），

∴AB=CD，∠ACD=∠CAB，

23、两个边长分别为a和b的正方形如图放置（图1），其未叠合部分，（阴影）面积为S1：若再在图1中大正方形的右下角摆放一个边长为b的小正方形，两个小正方形叠合部分（阴影）面积为S2,。

（1）用含a、b的代数式分别表示S1，S2

（2）若a+b=16,ab=40,求S1+S2的值

           图1                               图2

答案：解

（1）S1=a²-b²

     S2=b（2b-a）=2b²-ab

S1+S2=a²+b²-ab=（a+b）²-ab=256-40=216

答：S1+S2为216

24、如图24-1，已知线段AB、CD相交于点O，连接AC、BD，我们把形如图1图形称之为“8字形”，已知∠A+∠C=∠B+∠D，如图24-2，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N，试解答下列问题：

（1）如图2中，若∠B=96°，∠C=100°，求∠P的度数；

（2）在图2中，若∠CAP=∠BAC，∠CDP=∠BDC，试问∠P与∠C、∠B之间的数量关系为             

答案：

（1）

解：∵∠CAB和∠BDC的平分线AP和DP相交于点P，

∴∠CAP=∠BAP，∠BDP=∠CDP，

∵∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，

∴∠C-∠P=∠P-∠B，

即∠P=（∠C+∠B），

∵∠C=100°，∠B=96°，

∴∠P=（100°+96°）=98°；

（2）

解：结论：∠P=（∠B+2∠C），

理由：∵∠CAP=∠CAB，∠CDP=∠CDB，

∴∠BAP=∠BAC，∠BDP=∠BDC，

∵∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，

∴∠C-∠P=∠BDC-∠BAC，∠P-∠B=∠BDC-∠BAC，

∴2（∠C-∠P）=∠P-∠B，

∴∠P=（∠B+2∠C），

25、如图，在四边形ABCD中，∠A=x，∠C=y

（1）∠ABC+∠ADC=        （含x，y的式子直接填空）；

（2）如图1，x=y=90°，DE平分∠ADC，BF平分∠CBM，请写出DE与BF的位置关系，并说明理由；

（3）如图2，∠DFB为四边形ABCD的∠ABC，∠ADC相邻的外角平分线所在直线构成的锐角。若x+y=120°，∠DFB=20°，求x、y的值

图1                             图2

【分析】（1）利用四边形的内角和进行计算即可；（2）由三角形外角的性质及角的平分线性质得出BF和DE的位置关系，进而作答；（3）①利用角平分线的定义以及三角形内角和定理，得出 ，进而得出x，y的值

【详解】，，，

．

故答案为．

．

理由：如图1，

平分，BF平分，

，，

又，

，

又，

，

；

由得：，

、DF分别平分、，

，

如图2，连接DB，

则，

，

，

解方程组：，

可得：；

【点睛】本题主要考查了多边形的内角和角平分线的定义以及三角形内角和定理等知识，正确应用角平分线的定义是解题关键.