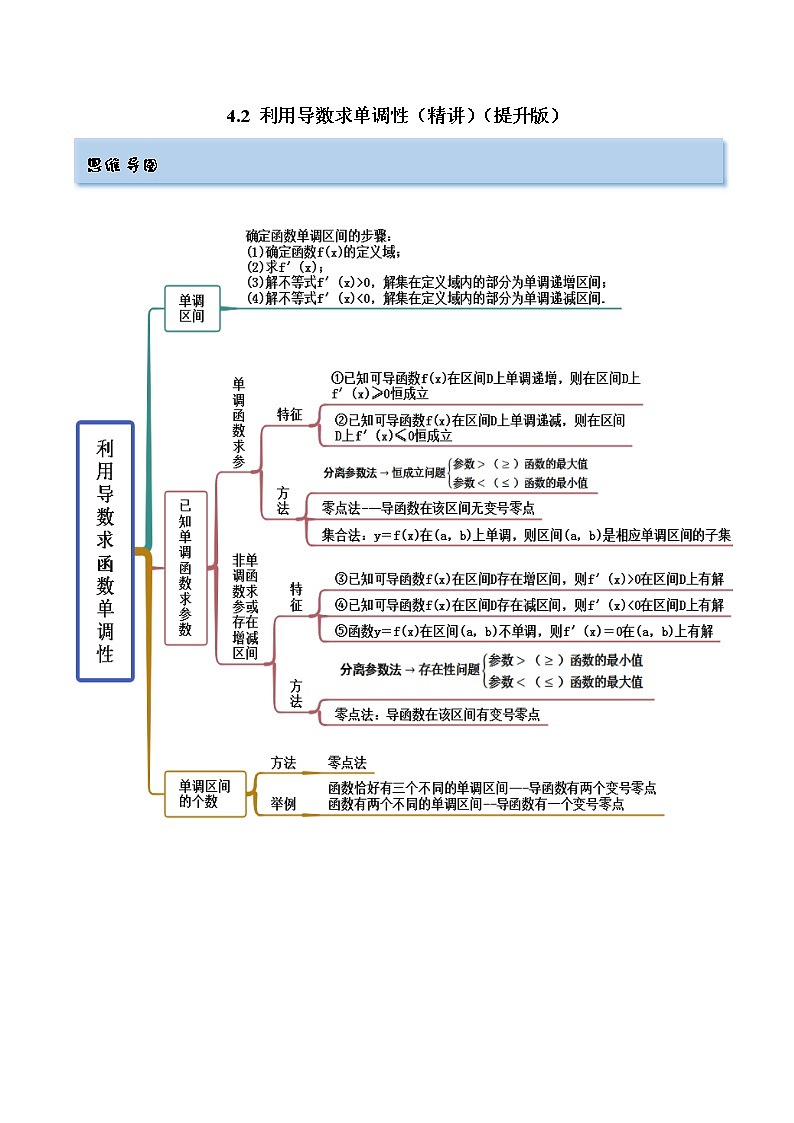
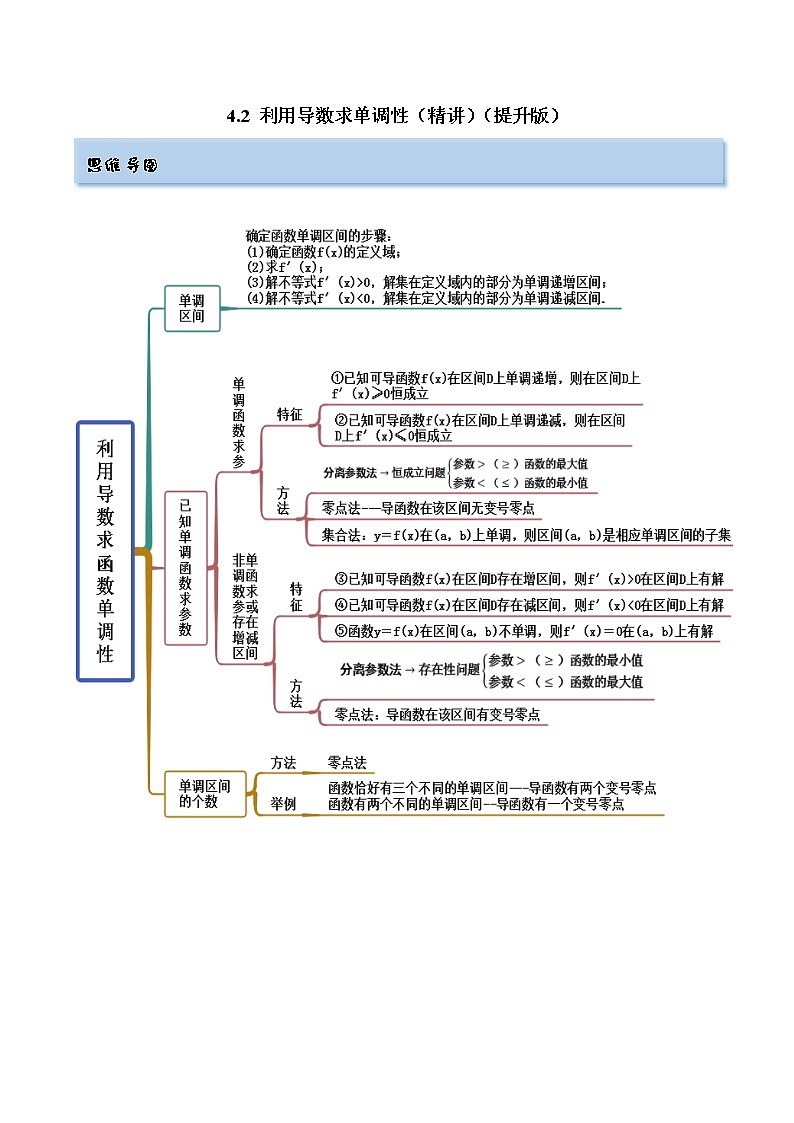
4.2 利用导数求单调性（精讲）- 2023年高考数学一轮复习（提升版）（新高考地区专用）

这是一份4.2 利用导数求单调性（精讲）- 2023年高考数学一轮复习（提升版）（新高考地区专用），文件包含42利用导数求单调性精讲提升版解析版docx、42利用导数求单调性精讲提升版原卷版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
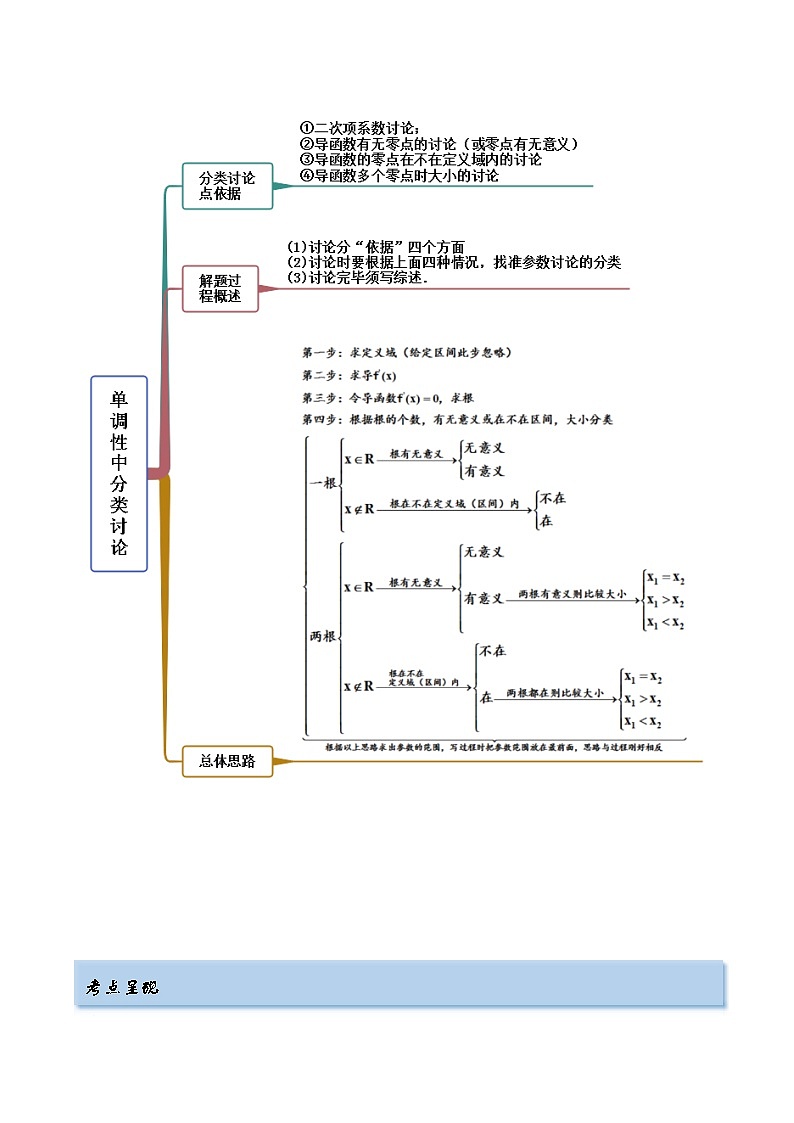
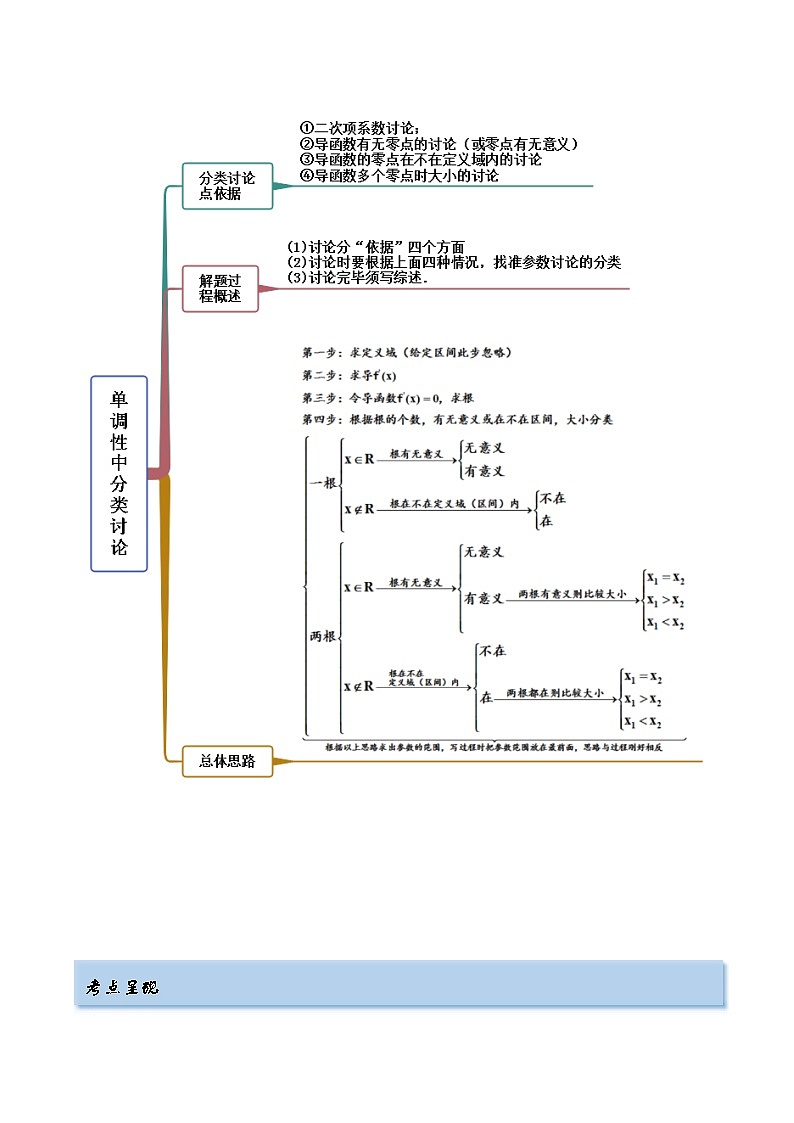
4.2 利用导数求单调性（精讲）（提升版）      考点一 单调区间（无参）【例1-1】（2022·新疆）函数的减区间是____________. 【例1-2】（2022·广东·顺德一中）设曲线在上的单调递减区间是______. 【例1-3】（江苏省苏州实验中学）已知函数f(x)满足，则f(x)的单调递减区间为（       ）A．(-∞,0) B．(1,+∞) C．(-∞,1) D．(0,+∞) 【一隅三反】1．函数f(x)＝x＋2的单调递增区间是(　　)A．(0,1)   B．(－∞，1)C．(－∞，0)   D．(0，＋∞) 2．（皖豫名校联盟体2022届）函数的单调递减区间为__________． 3．已知定义在区间(0，π)上的函数f(x)＝x＋2cos x，则f(x)的单调递增区间为        ． 考点二 已知单调性求参数【例2-1】（2022安徽省“皖东县中联盟）若函数在区间上单调递减，则实数a的取值范围是（       ）A． B． C． D． 【例2-2】（2022.广东）已知函数在区间上不是单调函数，则实数a的取值范围是（       ）A． B． C． D． 【一隅三反】1．（2022福建省）已知函数在上为单调递增函数，则实数m的取值范围为（       ）A． B． C． D． 2．（湖南省三湘名校教育联盟2022届）若是R上的减函数，则实数a的取值范围是（            ）A． B． C． D． 3．（江西省宜春市八校2022届）已知函数在区间上存在单调减区间，则实数的取值范围为（       ）A． B．C． D． 4．（2022·宁夏吴忠）已知函数存在三个单调区间，则实数的取值范围是（       ）A． B．C． D． 考点三 单调性的应用之解不等式【例3】（湖南省多所学校2022届）已知，则的解集是（       ）A．  B．或C．或  D．或 【一隅三反】1．（陕西省西安地区八校2022届）已知函数，则不等式的解集为（       ）A． B．C． D． 2．（湖北省2022届）已知函数，不等式的解集为（       ）A． B．C． D． 3．若函数f(x)＝ln x＋ex－sin x，则不等式f(x－1)≤f(1)的解集为        ． 4．已知函数f(x)＝xsin x＋cos x＋x2，则不等式f(ln x)＋f <2f(1)的解集为        ．   考点四 单调性应用之比较大小【例4-1】（华大新高考联盟名校2022届）已知实数a，b，，e为自然对数的底数，且，，，则（       ）A． B．C． D． 【例4-2】（湖南师范大学附中2022届）下列两数的大小关系中正确的是（     ）A． B．C． D． 【一隅三反】1．（2022年全国新高考I卷数学试题）设，则（       ）A． B． C． D． 2．（山东省青州市2022届）设，，，则（       ）A． B． C． D． 3．（江西省萍乡市2022届）设，，，则（       ）A． B．C． D． 4．（湖北省二十一所重点中学2022届）已知是自然对数的底数，设，，，，下列说法正确的是（       ）A． B．C． D． 考点五 含参函数的单调性讨论【例5-1】（2022广西节选）已知函数，讨论的单调性；        【例5-2】（2022安徽）已知函数，讨论f（x）的单调性；        【例5-3】（安徽省江淮名校2022届）已知函数，讨论的单调性；        【例5-4】（2022辽宁省沈阳市第二中学）已知函数，讨论的单调性；         【一隅三反】1．（2022贵州省贵阳市五校）已知，函数，讨论的单调性；        2．（2022陕西省）已知函数．讨论函数的单调性；       3．（重庆市第八中学校2022届高三下学期适应性月考（七）数学试题）已知，讨论的单调性；              4．（2022江苏省）已知函数，函数的导函数为．讨论函数的单调性；