广东省深圳市高级中学2021-2022学年七年级下学期期末测试数学试卷(含答案)

高级中学2021- 2022学年第二学期期末测试

初一数学

一、选择题： (每小题只有一个选项，每小题3分，共计30分)

1. 下列2022年北京冬奥会吉祥物冰墩墩的图形中，是轴对称图形的是（    ）．

A.  B.  

C.  D.

2. 如图是一个由5个相同正方体组成的立体图形，从其正面看，得到的平面图形是（    ）

A.  B.  

C.  D.

3. 今年4月16日，神舟十三号载人飞船返回舱在东风着陆场预定区域安全着陆，三位航天员顺利返回地面，神舟十三号载人飞行任务取得圆满成功．已知神舟十三号飞行过程中近地距离，远地距离．将“356000”用科学记数法表示为（    ）

A.  B.  

C.  D.

4. 下列运算正确是(      )

A. (2a2)3 =6a6 B. 2a2 +3a2 = 5a4 C. a3÷a-1=a4 D. a4．a2=a8

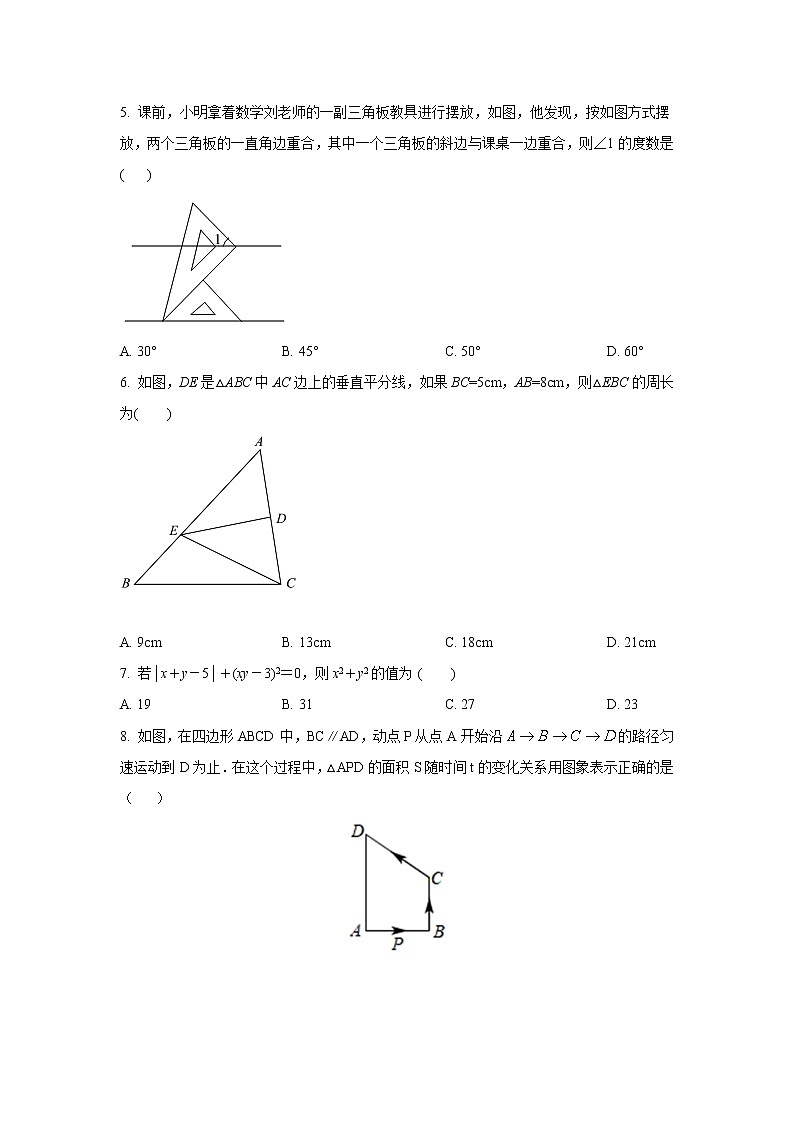
5. 课前，小明拿着数学刘老师的一副三角板教具进行摆放，如图，他发现，按如图方式摆放，两个三角板的一直角边重合，其中一个三角板的斜边与课桌一边重合，则∠1的度数是(    )

A. 30° B. 45° C. 50° D. 60°

6. 如图，DE是△ABC中AC边上的垂直平分线，如果BC=5cm，AB=8cm，则△EBC的周长为(     )

A. 9cm B. 13cm C. 18cm D. 21cm

7. 若│x＋y－5│＋(xy－3)2＝0，则x2＋y2的值为 (     )

A. 19 B. 31 C. 27 D. 23

8. 如图，在四边形ABCD中，BC∥AD，动点P从点A开始沿的路径匀速运动到D为止．在这个过程中，△APD的面积S随时间t的变化关系用图象表示正确的是（    ）

A.  B.  

C.  D.

9. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为(   )

A. 2.2米 B. 2.3米 C. 2.4米 D. 2.5米

10. 如图，在△ABC中，∠BAC 和∠ABC的平分线AE， BF相交于点O， AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，在下列结论中：①∠AOB=90°+∠C；②若AB=4，OD=1，则S△ABO=2； ③当∠C=60°时，AF+BE=AB；④若OD=a，AB+BC+CA=2b，则S△ABC=ab．其中正确的结论个数为(    )

A. 1 B. 2

C. 3 D. 4

二．填空题(共5小题，每题3分，共15分)

11. 若am=8，an=2，则 的值是________

12. 如图．在△ABC中，∠C=90°，AD平分∠CAB， DE⊥AB于E，若CD=3，BD=5，则BE长为__________     

13. 七巧板是我国古代劳动人民的发明之一，被誉为“东方魔板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图是一个用七巧板拼成的正方形飞镖游戏板，某人向该游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是______．

14. 如图，Rt△ABC中，∠C=90°，AC=4，BC=3，点P为AC边上的动点，过点P作PD⊥AB于点D，则PB+PD的最小值为_____．

15. 如图，矩形ABCD中，AD＝6，AB＝8．点E为边DC上的一个动点，△AD'E与△ADE关于直线AE对称，当△CD'E为直角三角形时，DE的长为__．

三．解答题(共7小题，共55分)

16. 计算：（）-1-(π-3)0+(-23)-4×∣-1∣

17. 先化简，再求值：)，其中x=-1， y=2．

18. 如图：在正方形网格上有一个△ABC．

（1）画出△ABC关于直线MN的对称图形：

（2）△ABC的形状是          三角形；

（3）若在MN上存在一点P，使得PA+PC最小，请在图中画出点P的位置：

（4）若网格上最小正方形边长为1，求△ABC的面积．

19. 在一条东西走向的河的一侧有一村庄C，河边原有两个取水点A，B，其中，由于某种原由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得千米，千米，千米．

（1）问CH是否为从村庄C到河边的最近路？请通过计算加以说明．

（2）求原来的路线AC的长．

20. 甲乙两地的距离为45千米，下图中的折线表示某骑车人离甲地的距离y（千米）与时间x（时）之间的函数关系．有一辆客车9点从乙地出发，以45千米/小时的速度匀速行驶，并往返于甲乙两地之间（乘客上下车的停留时间忽略不计）．

（1）从折线图可以看出，骑车人一共休息_______次，共休息了_________小时；

（2）请在图中画出9点至15点之间客车与甲地的距离y（千米）随时间x（时）变化的函数图象；

（3）由图象可以看出，在_______时，骑车人与客车同时位于________地（填“甲”或“乙”），除此之外行进过程中，有_____次是骑车人与客车迎面相遇，有________次是客车从背后追上骑车人．

21. 已知四边形ABCD中，BC=CD，连接BD，过点C作BD垂线交AB于点E，连接DE．

（1）如图1，若DCBE，求证：DB平分∠CDE；

（2）如图2，连接AC，设BD， AC相交于点F，DE垂直平分线段AC．

(i)求∠CED的大小；

(ii)若AF=AE，求证：BE=CF．

22. 在△ABC中，点D，E分别为边BC，AC上一个动点，连接AD，BE．

（1）已知∠ABC＝∠C，线段AD与BE交于点O，且满足∠AOE＝∠AEO．

①如图1，若∠BAC＝60°，AD平分∠BAC，则∠EBC的度数为 　 　．（直接写出答案）

②如图2，猜想∠BAD与∠CBE之间的数量关系，并证明．

（2）如图3，AD，BE都为△ABC的高，点G，点F分别在线段AD和射线BE上，且满足AG＝BC，BF＝AC，过点F作FM⊥AB于M，过点G作GN⊥AB于点N，猜想FM，GN和AB之间的数量关系，并证明．

答案

1-10 BABCB  BADAC 

11. 1

12. 4

13.

14.

15. 3或6

16. 解：原式 ．

17. 解：原式

．

当，时，

原式

．

18. 【小问1详解】

解：如图，△A′B′C′为所作；

；

【小问2详解】

解：在△ACF和△CBE中，

，

∴△ACF≌△CBE(SAS)，

∴AC=BC，∠ACF=∠CBE，

∵∠CBE+∠BCE=90°，

∴∠ACF+∠BCE=90°，

∴∠BCA=90°，

∴△ABC等腰直角三角形；

故答案为：等腰直角；

【小问3详解】

解：如图，点P为所作；

【小问4详解】

解：△ABC的面积=3×4-×1×3-×1×3-×4×2=5．

19. 小问1详解】

解：是， 理由是：在△CHB中，

∵CH2+BH2=1.22+0.92=2.25， BC2=2.25，

∴CH2+BH2=BC2，

∴△CHB是直角三角形，

∴CH是从村庄C到河边的最近路；

【小问2详解】

设AC=x千米，

在Rt△ACH中，由已知得AC=x，AH=x-0.9，CH=1.2，

由勾股定理得：AC2=AH2+CH2

∴x2=（x-0.9）2+1.22，

解这个方程，得x=1.25，

答：原来的路线AC的长为1.25千米．

20. 解：（1）根据题意得：骑车人一共休息2次，共休息了（11-10）+（13-12）=2时；

（2）根据题意得：客车从乙地到甲地所用的时间为 （时），

所以9点至15点之间客车在甲乙两地之间往返 次，

则9点至15点之间客车与甲地的距离y（千米）随时间x（时）变化的函数图象，如图所示，

（3）由图象可以看出，在13时，骑车人与客车同时位于乙地；

二者迎面相遇，是客车从乙地驶往甲地的过程中，此时y（千米）随时间x（时）的增大而减小，由图象可以看出，除此之外的行进过程中，在9时到10时之间，11时至12时之间，14时至15时之间的3次相遇是骑车人与客车迎面相遇；

客车从背后追上骑车人，是客车从甲地驶往乙地的过程中，此时y（千米）随时间x（时）的增大而增大，在10至11时之间的1次相遇是客车从背后追上骑车人．

21. 【小问1详解】

证明：设与交于点，

，，

，

，

，

，

，

，

四边形是平行四边形，

，

平行四边形是菱形；

DB平分∠CDE；

【小问2详解】

解：解：垂直平分，

且，

，

又且，

垂直平分，

，

，

，

又，

；

证明：由得，

又，

，

同理可得，在等腰中，，

，

在与中，

，

，

，

又，

，

即．

22. 解：（1）①且AD平分∠BAC，根据已知证，然后再证明

∴，且，

，

故答案为：；

②；证明如下：

，且，

，

，

，

，

又，

，且，

；

（2）如图，作交AB于H点，

则AD、BE、CH交于点I，

，

，

，

，

，

又，且，

，

，

,

,

又,

,

又,且,

,

,

,

即．