中考冲刺：数形结合问题--巩固练习（基础）

这是一份中考冲刺：数形结合问题--巩固练习（基础），共8页。
选择题
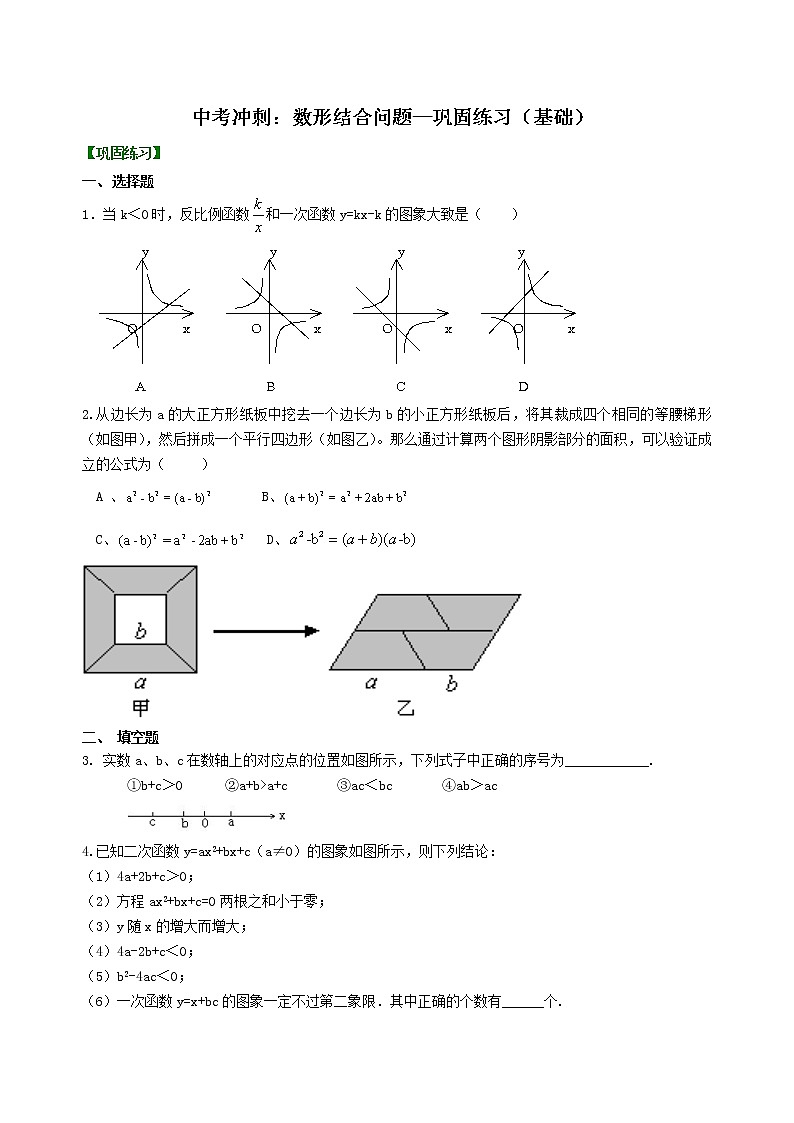
1．当k＜0时，反比例函数和一次函数y=kx-k的图象大致是（ ）
2.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）。那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）
A 、 B、
C、 D、
二、 填空题
3. 实数a、b、c在数轴上的对应点的位置如图所示，下列式子中正确的序号为____________.
①b+c＞0 ②a+b>a+c ③ac＜bc ④ab＞ac
4.已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：
（1）4a+2b+c＞0；
（2）方程ax2+bx+c=0两根之和小于零；
（3）y随x的增大而增大；
（4）4a-2b+c＜0；
（5）b2-4ac＜0；
（6）一次函数y=x+bc的图象一定不过第二象限．其中正确的个数有______个.
三、解答题
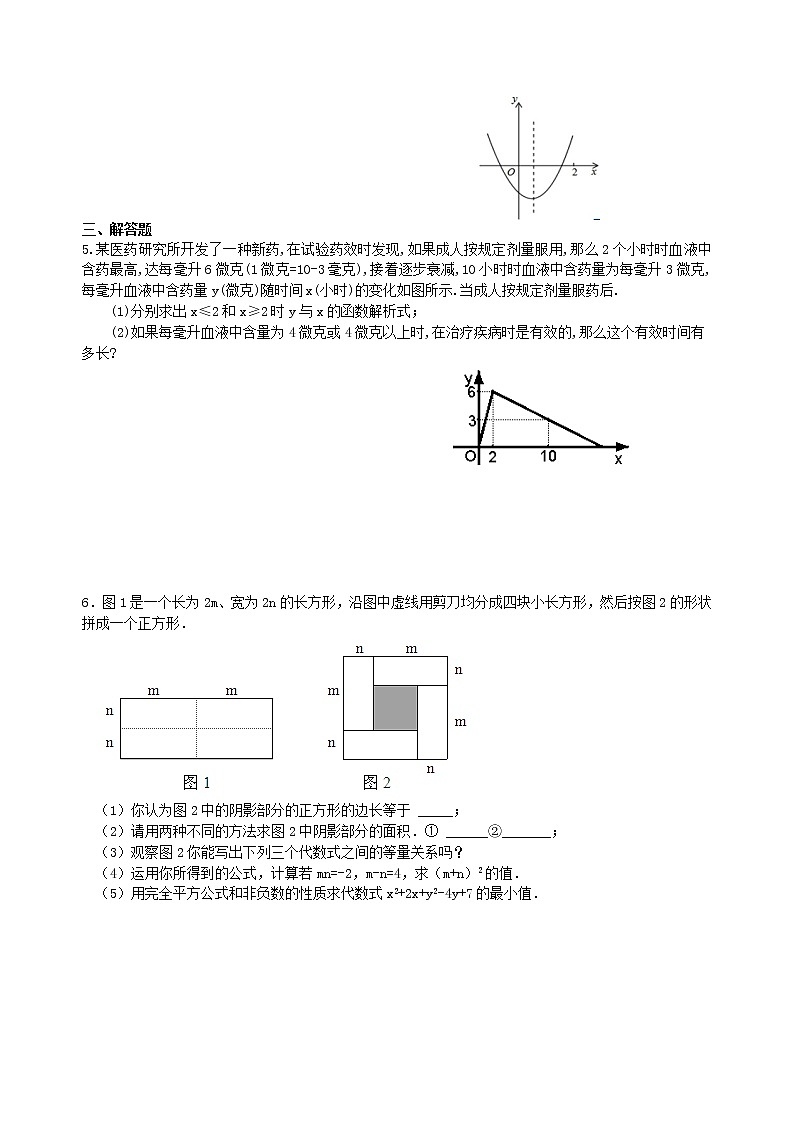
5.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么2个小时时血液中含药最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时y与x的函数解析式；
(2)如果每毫升血液中含量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间有
多长?
6．图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

（1）你认为图2中的阴影部分的正方形的边长等于 _____；
（2）请用两种不同的方法求图2中阴影部分的面积．① ______②_______；
（3）观察图2你能写出下列三个代数式之间的等量关系吗？
（4）运用你所得到的公式，计算若mn=-2，m-n=4，求（m+n）2的值．
（5）用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值．
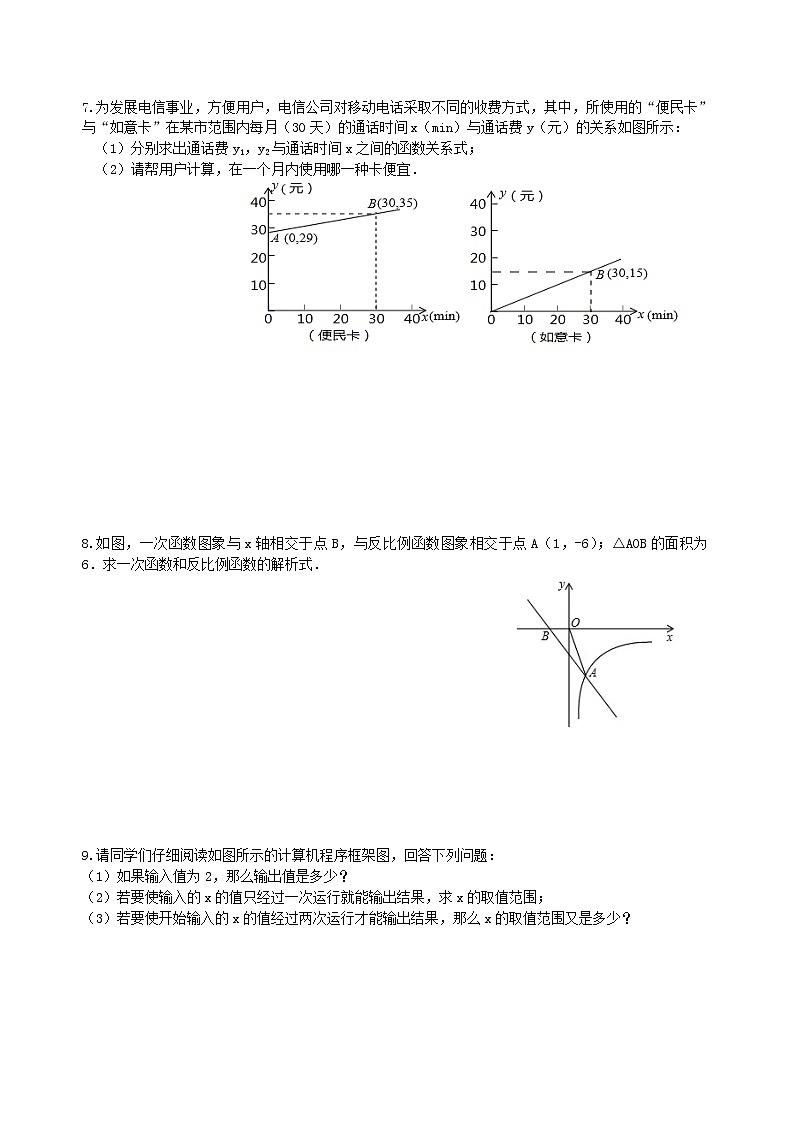
7.为发展电信事业，方便用户，电信公司对移动电话采取不同的收费方式，其中，所使用的“便民卡”与“如意卡”在某市范围内每月（30天）的通话时间x（min）与通话费y（元）的关系如图所示：
（1）分别求出通话费y1，y2与通话时间x之间的函数关系式；
（2）请帮用户计算，在一个月内使用哪一种卡便宜．

8.如图，一次函数图象与x轴相交于点B，与反比例函数图象相交于点A（1，-6）；△AOB的面积为6．求一次函数和反比例函数的解析式．
9.请同学们仔细阅读如图所示的计算机程序框架图，回答下列问题：
（1）如果输入值为2，那么输出值是多少？
（2）若要使输入的x的值只经过一次运行就能输出结果，求x的取值范围；
（3）若要使开始输入的x的值经过两次运行才能输出结果，那么x的取值范围又是多少？
10.观察如图所包含规律（图中三角形均是直角三角形，且一条直角边始终为1，四边形均为正方形．S1，S2，S3，…Sn依次表示正方形的面积，每个正方形边长与它左边相邻的直角三角形斜边相等），再回答下列问题．
（1）填表：
（2）当s1+s2+s3+s4+…+sn=465时，求n．
11.某报社为了了解读者对该报社一种报纸四个版面的认可情况，对读者做了一次问卷凋查，要求读者选出自己最喜欢的一个版面，并将调查结果绘制成如下的统计图，请你根据图中提供的信息解答下列问题．
（1）在这次活动中一共调查了多少读者？
（2）在扇形统计图中，计算第一版所在扇形的圆心角度数；
（3）请你求出喜欢第四版的人数，并将条形统计图补充完整．

【答案与解析】
一、选择题
1．【答案】B；
2．【答案】D；
二、 填空题
3．【答案】②③④；
4．【答案】1；
三、 解答题
5．【答案与解析】
解：（1）当x≤2时，设y=kx，
把（2，6）代入上式，得k=3，
∴x≤2时，y=3x；
当x≥2时，设y=kx+b，
把（2，6），（10，3）代入上式，得
k=，b=
∴x≥2时，y=x+
（2）把y=4代入y=3x，得x1=
把y=4代入y=x+ 得x2=
则x2-x1=6（小时）．
答：这个有效时间为6小时．
6．【答案与解析】
解：（1）由图可知，阴影部分小正方形的边长为：m-n；
（2）根据正方形的面积公式，阴影部分的面积为（m-n）2，
还可以表示为（m+n）2-4mn；
（3）根据阴影部分的面积相等，（m-n）2=（m+n）2-4mn；
（4）∵mn=-2，m-n=4，
∴（m+n）2=（m-n）2+4mn=42+4×（-2）=16-8=8；
（5）x2+2x+y2-4y+7，
=x2+2x+1+y2-4y+4+2，
=（x+1）2+（y-2）2+2，
∵（x+1）2≥0，（y-2）2≥0，
∴（x+1）2+（y-2）2≥2，
∴当x=-1，y=2时，代数式x2+2x+y2-4y+7的最小值是2．
故答案为：（1）m-n；（2）（m-n）2，（m+n）2-4mn；（3）（m-n）2=（m+n）2-4mn．(4) 8 (5) 最
小值是2.
7.【答案与解析】
解：（1）设y1=kx+b，将（0，29），（30，35）代入，
解得k=，b=29，∴y1=x+29，
又24×60×30=43200（min）（属于隐含条件）
∴y1=x+29 （0≤x≤43200），
同样求得y2=x (0≤x≤43200)；
（2）当y1=y2时，
x+29=x，
x=；
当y1＜y2时，
x+29＜x， x＞．
所以，当通话时间等于min时，两种卡的收费一致，
当通话时间小于min时，“如意卡便宜”，
当通话时间大于min时，“便民卡”便宜．
8.【答案与解析】
解：设反比例函数解析式为：y=（k≠0），
∵点A（1，-6）在反比例函数图象上
∴k=1×（-6）=-6，
即反比例函数关系式为y=-，
∵△AOB的面积为6．
∴×OB×6=6，
∴OB=2，
∴B（-2，0），
设一次函数解析式为：y=kx+b，
∵图象经过A（1，-6），B（-2，0），
∴
解得：
∴一次函数解析式为：y=-2x-4．
9.【答案与解析】
解：（1）依据题中的计算程序列出算式：3×2+1，
∵3×2+1=7，7＜9，
∴应该按照计算程序继续计算，3×7+1=22＞9，
∴如果输入值为2，那么输出值是22．
（2）依题意，有3x+1＞9，
解得x＞；
（3）依题意，有
解得＜x≤.
10.【答案与解析】
解：(1)，
，
（2）S1=（）2=2，
S2=（）2=3，
S3=22=4，
S4=（）2=5，……..
Sn=（）2=n+1；
由s1+s2+s3+s4+…+sn=465可得：
1+2+3+4+5+…+n=465，
(1+n) ×n=465
解得：n=-31（不合题意舍去）或n=30，
故：n=30．
11.【答案与解析】
解：（1）这次活动中一共调查了500÷10%=5000（人）；
（2）第一版所在扇形的圆心角度数=360°×（1-20%-40%-10%）=108°；
（3）喜欢第四版的人数是：
5000×20%=1000（人），如下图所示：

直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
…
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
2
…