初中数学9上九月份 学月检测题含答案

九年级上册九月份 学月检测题（1）

姓名：__________班级：__________考号：__________

一    、选择题（本大题共12小题，每小题4分，共48分）

1.下列方程中，一元二次方程共有（　　）个

①x2﹣2x﹣1=0；②ax2+bx+c=0；③ +3x﹣5=0；④﹣x2=0；

⑤（x﹣1）2+y2=2；   ⑥（x﹣1）（x﹣3）=x2．

A．1 B．2 C．3 D．4

2.把二次函数y=x2﹣4x+1化成y=a（x+m）2+k的形式是（　　）

A．y=（x﹣2）2+1           B．y=（x﹣2）2﹣1

C．y=（x﹣2）2+3                    D．y=（x﹣2）2﹣3

3.随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2015年底某市汽车拥有量为16.9万辆．己知2013年底该市汽车拥有量为10万辆，设2013年底至2015年底该市汽车拥有量的平均增长率为x，根据题意列方程得（　　）

A．10（1+x）2=16.9 B．10（1+2x）=16.9

C．10（1﹣x）2=16.9          D．10（1﹣2x）=16.9

4.抛物线y=（x﹣3）2﹣1的顶点坐标是（　　）

A．（3，1） B．（3，﹣1） C．（﹣3，1） D．（﹣3，﹣1）

5.已知关于x的一元二次方程x2+mx﹣8=0的一个实数根为2，则另一实数根及m的值分别为（　　）

A．4，﹣2 B．﹣4，﹣2 C．4，2 D．﹣4，2

6.抛物线y=﹣4x2+5的开口方向（　　）

A．向上 B．向下 C．向左 D．向右

7.在下列二次函数中，其图象对称轴为x=2的是（　　）

A．y=2x2﹣4 B．y=2（x﹣2）2 C．y=2x2+2 D．y=2（x+2）2

8.已知关于x的一元二次方程x2+2x﹣（m﹣2）=0有实数根，则m的取值范围是（　　）

A．m＞1 B．m＜1 C．m≥1 D．m≤1

9.方程x2+x﹣12=0的两个根为（　　）

A．x1=﹣2，x2=6 B．x1=﹣6，x2=2 C．x1=﹣3，x2=4 D．x1=﹣4，x2=3

10.在同一坐标系中，一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是（　　）

11.给出一种运算：对于函数y=xn，规定y′=nxn﹣1．例如：若函数y=x4，则有y′=4x3．已知函数y=x3，则方程y′=12的解是（　　）

A．x1=4，x2=﹣4 B．x1=2，x2=﹣2 C．x1=x2=0 D．x1=2，x2=﹣2

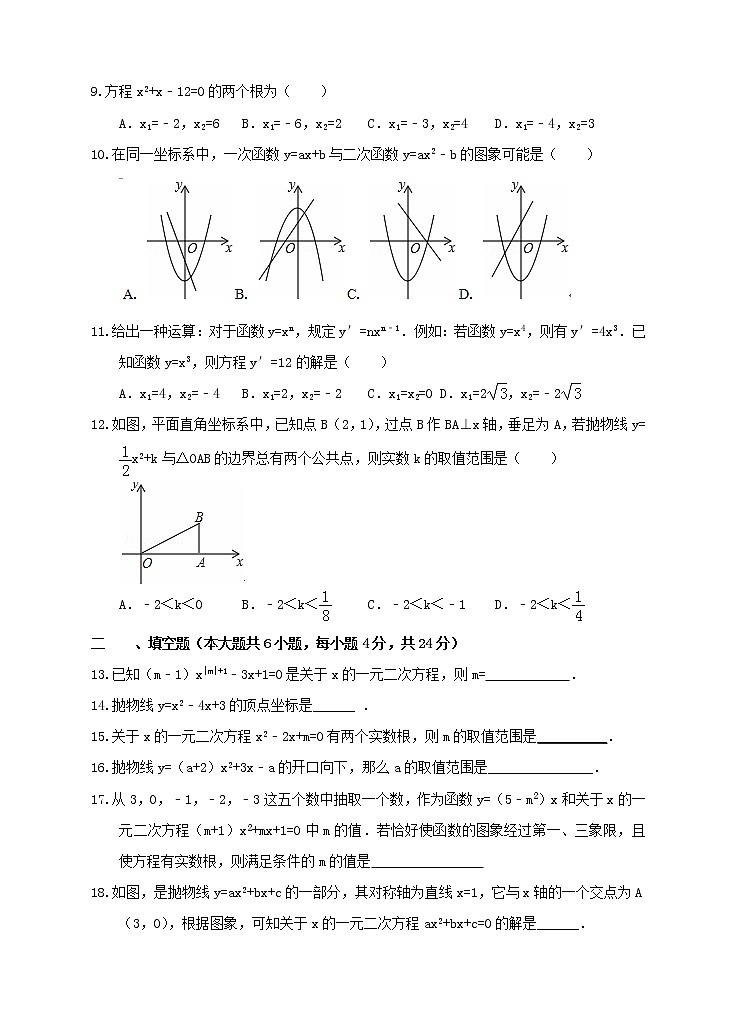
12.如图，平面直角坐标系中，已知点B（2，1），过点B作BA⊥x轴，垂足为A，若抛物线y=x2+k与△OAB的边界总有两个公共点，则实数k的取值范围是（　　）

A．﹣2＜k＜0 B．﹣2＜k＜ C．﹣2＜k＜﹣1 D．﹣2＜k＜

二    、填空题（本大题共6小题，每小题4分，共24分）

13.已知（m﹣1）x|m|+1﹣3x+1=0是关于x的一元二次方程，则m=　　　　　　．

14.抛物线y=x2﹣4x+3的顶点坐标是______ ．

15.关于x的一元二次方程x2﹣2x+m=0有两个实数根，则m的取值范围是__________．

16.抛物线y=（a+2）x2+3x﹣a的开口向下，那么a的取值范围是_______________．

17.从3，0，﹣1，﹣2，﹣3这五个数中抽取一个数，作为函数y=（5﹣m2）x和关于x的一元二次方程（m+1）x2+mx+1=0中m的值．若恰好使函数的图象经过第一、三象限，且使方程有实数根，则满足条件的m的值是　             

18.如图，是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=1，它与x轴的一个交点为A（3，0），根据图象，可知关于x的一元二次方程ax2+bx+c=0的解是______．

三    、解答题（本大题共8小题，19-20每题7分，21-24每题10分，24-25每题12分，共78分）

19.（1）解方程：x2﹣4x+3=0；           （2）解不等式组．

20.已知抛物线y=﹣x2+bx+c的对称轴是直线x=﹣1，且经过点（2，﹣3），求这个二次函数的表达式．

21.关于x的方程3x2+mx﹣8=0有一个根是，求另一个根及m的值．

22.某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

（1）求y与x之间的函数关系式；

（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

23.在直角墙角AOB（OA⊥OB，且OA．OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m2．

（1）求这地面矩形的长；

（2）有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？

24.已知关于x的一元二次方程x2﹣2x+k=0．

（1）若方程有实数根，求k的取值范围；

（2）如果k是满足条件的最大的整数，且方程x2﹣2x+k=0一根的相反数是一元二次方程（m﹣1）x2﹣3mx﹣7=0的一个根，求m的值及这个方程的另一根．

25.九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．

（1）求出w与x的函数关系式；

（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；

（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．

26.正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．

（1）建立适当的平面直角坐标系，

①直接写出O、P、A三点坐标；

②求抛物线L的解析式；

（2）求△OAE与△OCE面积之和的最大值．

0.九年级上册九月份 学月检测题（1）答案解析

一    、选择题

1.【考点】一元二次方程的定义．

【分析】本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证．

【解答】解：①x2﹣2x﹣1=0，符合一元二次方程的定义；

②ax2+bx+c=0，没有二次项系数不为0这个条件，不符合一元二次方程的定义；

③+3x﹣5=0不是整式方程，不符合一元二次方程的定义；

④﹣x2=0，符合一元二次方程的定义；

⑤（x﹣1）2+y2=2，方程含有两个未知数，不符合一元二次方程的定义；

⑥（x﹣1）（x﹣3）=x2，方程整理后，未知数的最高次数是1，不符合一元二次方程的定义．

一元二次方程共有2个．

故选：B．

【点评】本题考查了一元二次方程的概念，判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是2．

2.【考点】二次函数的三种形式．

【分析】运用配方法把二次函数的一般式化为顶点式即可．

【解答】解：y=x2﹣4x+1

=x2﹣4x+4﹣3

=（x﹣2）2﹣3，

故选：D．

3.【分析】根据题意可得：2013年底该市汽车拥有量×（1+增长率）2=2015年底某市汽车拥有量，根据等量关系列出方程即可．　　

【解答】解：设2013年底至2015年底该市汽车拥有量的平均增长率为x，

根据题意，可列方程：10（1+x）2=16.9，

故选：A．

【点评】此题主要考查了由实际问题抽象出一元二次方程，关键是掌握平均变化率的方法，若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．

4. 【考点】二次函数的性质．

【分析】根据二次函数的顶点式，可得顶点坐标．

【解答】解：由y=（x﹣3）2﹣1得顶点坐标是（3，﹣1），

故选：B．

5.【分析】根据题意，利用根与系数的关系式列出关系式，确定出另一根及m的值即可．

【解答】解：由根与系数的关系式得：2x2=﹣8，2+x2=﹣m=﹣2，

解得：x2=﹣4，m=2，

则另一实数根及m的值分别为﹣4，2，

故选D

【点评】此题考查了根与系数的关系式，熟练掌握一元二次方程根与系数的关系是解本题的关键．

6.【考点】二次函数的性质．

【分析】根据抛物线y=﹣4x2+5，可知二次项系数是﹣4，从而可以得到该函数的开口方向．

【解答】解：∵抛物线y=﹣4x2+5，﹣4＜0，

∴该抛物线的开口向下，

故选B．

7.【考点】二次函数的性质．

【分析】根据二次函数的性质求出各个函数的对称轴，选出正确的选项．

【解答】解：A．y=2x2﹣4的对称轴为x=0，所以选项A错误；

B、y=2（x﹣2）2的对称轴为x=2，所以选项B正确；

C、y=2x2+2的对称轴为x=0，所以选项C错误；

D、y=2（x+2）2对称轴为x=﹣2，所以选项D错误；

故选B．

8.【分析】根据关于x的一元二次方程x2+2x﹣（m﹣2）=0有实数根，可知△≥0，从而可以求得m的取值范围．

【解答】解：∵关于x的一元二次方程x2+2x﹣（m﹣2）=0有实数根，

∴△=b2﹣4ac=22﹣4×1×[﹣（m﹣2）]≥0，

解得m≥1，

故选C．

【点评】本题考查根的判别式，解题的关键是明确当一元二次方程有实数根时，△≥0．

9.【考点】解一元二次方程-因式分解法．

【分析】将x2+x﹣12分解因式成（x+4）（x﹣3），解x+4=0或x﹣3=0即可得出结论．

【解答】解：x2+x﹣12=（x+4）（x﹣3）=0，

则x+4=0，或x﹣3=0，

解得：x1=﹣4，x2=3．

故选D．

10.【考点】二次函数的图象；一次函数的图象．

【分析】先由一次函数y=ax+b图象得到字母a、b的正负，再与二次函数y=ax2﹣b的图象相比较看是否一致．

【解答】解：A．由直线y=ax+b的图象经过第二、三、四象限可知：a＜0，b＜0，

二次函数y=ax2﹣b的图象开口向上，

∴a＞0，A不正确；

B、由直线y=ax+b的图象经过第一、二、三象限可知：a＞0，b＞0，

二次函数y=ax2﹣b的图象开口向下，

∴a＜0，B不正确；

C、由直线y=ax+b的图象经过第一、二、四象限可知：a＜0，b＞0，

二次函数y=ax2﹣b的图象开口向上，

∴a＞0，C不正确；

D、由直线y=ax+b的图象经过第一、二、三象限可知：a＞0，b＞0，

二次函数y=ax2﹣b的图象开口向上，顶点在y轴负半轴，

∴a＞0，b＞0，D正确．

故选D．

11.【分析】首先根据新定义求出函数y=x3中的n，再与方程y′=12组成方程组得出：3x2=12，用直接开平方法解方程即可．

【解答】解：由函数y=x3得n=3，则y′=3x2，

∴3x2=12，

x2=4，

x=±2，

x1=2，x2=﹣2，

故选B．

【点评】本题考查了利用直接开平方法解一元二次方程，同时还以新定义的形式考查了学生的阅读理解能力；注意：①二次项系数要化为1，②根据平方根的意义开平方时，是两个解，且是互为相反数，不要丢解．

12.【考点】二次函数图象上点的坐标特征．

【分析】先根据抛物线解析式y=x2+k，求出抛物线与△AOB有一个公共点时的k值，然后根据抛物线的位置与开口方向判断k的取值范围即可．

【解答】解：①由B（2，1）可得，OB的解析式为y=x，

∵抛物线为y=x2+k，

∴当抛物线与OB有两个交点时，

一元二次方程x=x2+k中，判别式△＞0，

即1﹣8k＞0，

解得k＜，

∴抛物线与△OAB有两个公共点时，k＜；

②∵B（2，1），BA⊥x轴，

∴A（2，0），

当抛物线y=x2+k经过点A时，0=2+k，即k=﹣2，

∵抛物线开口向上，

∴抛物线与△OAB有两个公共点时，k＞﹣2，

综上，若抛物线y=x2+k与△OAB的边界总有两个公共点，则实数k的取值范围是﹣2＜k＜．

故选（B）

二    、填空题

13.【考点】一元二次方程的定义．

【分析】直接利用一元二次方程的定义得出|m|=1，m﹣1≠0，进而得出答案．

【解答】解：∵方程（m﹣1）x|m|+1﹣3x+1=0是关于x的一元二次方程，

∴|m|=1，m﹣1≠0，

解得：m=﹣1．

故答案为：﹣1．

【点评】此题主要考查了一元二次方程的定义，正确把握未知数的次数与系数是解题关键．

14.【考点】二次函数的性质．

【分析】根据抛物线y=x2﹣4x+3，可以将此函数的解析式化为顶点式，从而可以得到它的顶点坐标，本题得以解决．

【解答】解：∵y=x2﹣4x+3=（x﹣2）2﹣1，

∴抛物线y=x2﹣4x+3的顶点坐标是（2，﹣1），

故答案是：（2，﹣1）．

15.【考点】根的判别式．

【分析】根据方程有实数根，得出△≥0，建立关于m的不等式，求出m的取值范围即可．

【解答】解：由题意知，△=4﹣4m≥0，

∴m≤1，

故答案为：m≤1．

【点评】此题考查了根的判别式，掌握一元二次方程根的情况与判别式△的关系：△＞0⇔方程有两个不相等的实数根；△=0⇔方程有两个相等的实数根；△＜0⇔方程没有实数根是本题的关键．

16.【考点】二次函数的性质；二次函数的定义．

【分析】根据抛物线y=（a+2）x2+3x﹣a的开口向下，可得a+2＜0，从而可以得到a的取值范围．

【解答】解：∵抛物线y=（a+2）x2+3x﹣a的开口向下，

∴a+2＜0，

得a＜﹣2，

故答案为：a＜﹣2．

17.考点：    一次函数图象与系数的关系；根的判别式．.

分析：    确定使函数的图象经过第一、三象限的m的值，然后确定使方程有实数根的m值，找到同时满足两个条件的m的值即可．

解答：    解：∵函数y=（5﹣m2）x的图象经过第一、三象限，

∴5﹣m2＞0，

解得：﹣＜m＜，

∵关于x的一元二次方程（m+1）x2+mx+1=0有实数根，

∴m2﹣4（m+1）≥0，

∴m≥2+2或m≤2﹣2，

∴使函数的图象经过第一、三象限，且使方程有实数根的m的值有为﹣2，

故答案为：﹣2．

点评：    本题考查了一次函数图象与系数的关系及根的判别式的知识，解题的关键是会解一元二次不等式，难度不大．

18.【考点】抛物线与x轴的交点．

【分析】根据抛物线与x轴的两个交点到对称轴的距离相等，设另一个交点为（x，0），可得=1，解得x的值，关于x的一元二次方程ax2+bx+c=0的解就是抛物线与x轴交点的横坐标．

【解答】解：设抛物线与x轴的另一个交点坐标为：（x，0），

∵抛物线与x轴的两个交点到对称轴的距离相等，

∴=1，

解得：x=﹣1，

∴抛物线与x轴的另一个交点坐标为：（﹣1，0），

∴关于x的一元二次方程ax2+bx+c=0的解是3或﹣1．

三    、解答题

19.【考点】解一元二次方程-因式分解法；解一元一次不等式组．

【专题】计算题；一次方程（组）及应用．

【分析】（1）方程利用因式分解法求出解即可；

（2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可．

【解答】解：（1）分解因式得：（x﹣1）（x﹣3）=0，

可得x﹣1=0或x﹣3=0，

解得：x1=1，x2=3；

（2），

由①得：x≥1，

由②得：x＞2，

则不等式组的解集为x＞2．

【点评】此题考查了解一元二次方程﹣因式分解法，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．

20.考点：    待定系数法求二次函数解析式．

分析：    由抛物线的一般形式可知：a=﹣1，由对称轴方程x=﹣，可得一个等式﹣①，然后将点（2，﹣3）代入y=﹣x2+bx+c即可得到等式﹣4+2b+c=﹣3②，然后将①②联立方程组解答即可．

解答：    解：根据题意，得：，

解得，

所求函数表达式为y=﹣x2﹣2x+5．

点评：    此题考查了用待定系数法求二次函数的解析式，解题的关键是：熟练掌握待定系数法及对称轴表达式x=﹣．

21.【考点】根与系数的关系．

【分析】由于x=是方程的一个根，直接把它代入方程即可求出m的值，然后由根与系数的关系来求方程的另一根．

【解答】解：设方程的另一根为t．

依题意得：3×（）2+m﹣8=0，

解得m=10．

又t=﹣，

所以t=﹣4．

综上所述，另一个根是﹣4，m的值为10．

22.【考点】二次函数的应用．

【分析】（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．

（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．

（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．

【解答】解：（1）y=300+30（60﹣x）=﹣30x+2100．

（2）设每星期利润为W元，

W=（x﹣40）（﹣30x+2100）=﹣30（x﹣55）2+6750．

∴x=55时，W最大值=6750．

∴每件售价定为55元时，每星期的销售利润最大，最大利润6750元．

（3）由题意（x﹣40）（﹣30x+2100）≥6480，解得52≤x≤58，

当x=52时，销售300+30×8=540，

当x=58时，销售300+30×2=360，

∴该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装360件．

23.【考点】一元二次方程的应用．

【分析】（1）根据题意表示出长方形的长，进而利用长×宽=面积，求出即可；

（2）分别计算出每一规格的地板砖所需的费用，然后比较即可．

【解答】（1）设这地面矩形的长是xm，则依题意得：

x（20﹣x）=96，

解得x1=12，x2=8（舍去），

答：这地面矩形的长是12米；

（2）规格为0.80×0.80所需的费用：96×（0.80×0.80）×55=8250（元）．

规格为1.00×1.00所需的费用：96×（1.00×1.00）×80=7680（元）．

因为8250＜7680，

所以采用规格为1.00×1.00所需的费用较少．

24.【考点】根的判别式；一元二次方程的解．

【分析】（1）根据关于x的一元二次方程x2﹣2x+k=0有两个不等的实数根，得出4﹣4k≥0，即可求出k的取值范围；

（2）先求出k的值，再代入方程x2﹣2x+k=0，求出x的值，再把x的值的相反数代入（m﹣1）x2﹣3mx﹣7=0，即可求出m的值．

【解答】解：（1）∵关于x的一元二次方程x2﹣2x+k=0有两个不等的实数根，

∴△=b2﹣4ac=4﹣4k≥0，

解得：k≤1．

∴k的取值范围是k≤1；

（2）当k≤1时的最大整数值是1，

则关于x的方程x2﹣2x+k=0是x2﹣2x+1=0，

解得：x1=x2=1，

∵方程x2﹣2x+k=0一根的相反数是一元二次方程（m﹣1）x2﹣3mx﹣7=0的一个根，

∴当x=1时，（m﹣1）﹣3m﹣7=0，

解得：m=﹣4．

答：m的值是﹣4．

【点评】此题主要考查一元二次方程根的判别式，解题的关键是根据方程有实数根，求出k的值；一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．

25.【考点】二次函数的应用；一元一次不等式的应用．

【分析】（1）当0≤x≤50时，设商品的售价y与时间x的函数关系式为y=kx+b，由点的坐标利用待定系数法即可求出此时y关于x的函数关系式，根据图形可得出当50＜x≤90时，y=90．再结合给定表格，设每天的销售量p与时间x的函数关系式为p=mx+n，套入数据利用待定系数法即可求出p关于x的函数关系式，根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式；

（2）根据w关于x的函数关系式，分段考虑其最值问题．当0≤x≤50时，结合二次函数的性质即可求出在此范围内w的最大值；当50＜x≤90时，根据一次函数的性质即可求出在此范围内w的最大值，两个最大值作比较即可得出结论；

（3）令w≥5600，可得出关于x的一元二次不等式和一元一次不等式，解不等式即可得出x的取值范围，由此即可得出结论．

【解答】解：（1）当0≤x≤50时，设商品的售价y与时间x的函数关系式为y=kx+b（k、b为常数且k≠0），

∵y=kx+b经过点（0，40）、（50，90），

∴，解得：，

∴售价y与时间x的函数关系式为y=x+40；

当50＜x≤90时，y=90．

∴售价y与时间x的函数关系式为y=．

由书记可知每天的销售量p与时间x成一次函数关系，

设每天的销售量p与时间x的函数关系式为p=mx+n（m、n为常数，且m≠0），

∵p=mx+n过点（60，80）、（30，140），

∴，解得：，

∴p=﹣2x+200（0≤x≤90，且x为整数），

当0≤x≤50时，w=（y﹣30）•p=（x+40﹣30）（﹣2x+200）=﹣2x2+180x+2000；

当50＜x≤90时，w=（90﹣30）（﹣2x+200）=﹣120x+12000．

综上所示，每天的销售利润w与时间x的函数关系式是w=．

（2）当0≤x≤50时，w=﹣2x2+180x+2000=﹣2（x﹣45）2+6050，

∵a=﹣2＜0且0≤x≤50，

∴当x=45时，w取最大值，最大值为6050元．

当50＜x≤90时，w=﹣120x+12000，

∵k=﹣120＜0，w随x增大而减小，

∴当x=50时，w取最大值，最大值为6000元．

∵6050＞6000，

∴当x=45时，w最大，最大值为6050元．

即销售第45天时，当天获得的销售利润最大，最大利润是6050元．

（3）当0≤x≤50时，令w=﹣2x2+180x+2000≥5600，即﹣2x2+180x﹣3600≥0，

解得：30≤x≤50，

50﹣30+1=21（天）；

当50＜x≤90时，令w=﹣120x+12000≥5600，即﹣120x+6400≥0，

解得：50＜x≤53，

∵x为整数，

∴50＜x≤53，

53﹣50=3（天）．

综上可知：21+3=24（天），

故该商品在销售过程中，共有24天每天的销售利润不低于5600元．

26.【考点】二次函数综合题．

【分析】（1）以O点为原点，线段OA所在的直线为x轴，线段OC所在的直线为y轴建立直角坐标系．①根据正方形的边长结合正方形的性质即可得出点O、P、A三点的坐标；②设抛物线L的解析式为y=ax2+bx+c，结合点O、P、A的坐标利用待定系数法即可求出抛物线的解析式；

（2）由点E为正方形内的抛物线上的动点，设出点E的坐标，结合三角形的面积公式找出S△OAE+SOCE关于m的函数解析式，根据二次函数的性质即可得出结论．

【解答】解：（1）以O点为原点，线段OA所在的直线为x轴，线段OC所在的直线为y轴建立直角坐标系，如图所示．

①∵正方形OABC的边长为4，对角线相交于点P，

∴点O的坐标为（0，0），点A的坐标为（4，0），点P的坐标为（2，2）．

②设抛物线L的解析式为y=ax2+bx+c，

∵抛物线L经过O、P、A三点，

∴有，

解得：，

∴抛物线L的解析式为y=﹣+2x．

（2）∵点E是正方形内的抛物线上的动点，

∴设点E的坐标为（m，﹣+2m）（0＜m＜4），

∴S△OAE+SOCE=OA•yE+OC•xE=﹣m2+4m+2m=﹣（m﹣3）2+9，

∴当m=3时，△OAE与△OCE面积之和最大，最大值为9．