广东省2022年中考数学总复习讲练课件：题型循环卷8

这是一份广东省2022年中考数学总复习讲练课件：题型循环卷8，共28页。PPT课件主要包含了k＜2等内容，欢迎下载使用。

2．如图所示的几何体的主视图是(　　)
3．已知某新型感冒病毒的直径约为0.000 000 823米，将0.000 000 823用科学记数法表示为(　　)A．8.23×10－6B．8.23×10－7C．8.23×106D．8.23×107
4．下列图形中，既是轴对称图形又是中心对称图形的是(　　)
5．下列运算正确的是(　　)A．(x3)5＝x8B．(x－2)2＝x2－4C．2x2·x5＝2x7D．x3＋x5＝x86．一元二次方程x2＋4x－3＝0的两根为x1，x2，则x1＋x2＝(　　)A．4B．－4　　C．3D．－37．下列图形中，是中心对称图形，但不是轴对称图形的是(　　)A．正方形B．矩形C．菱形D．平行四边形
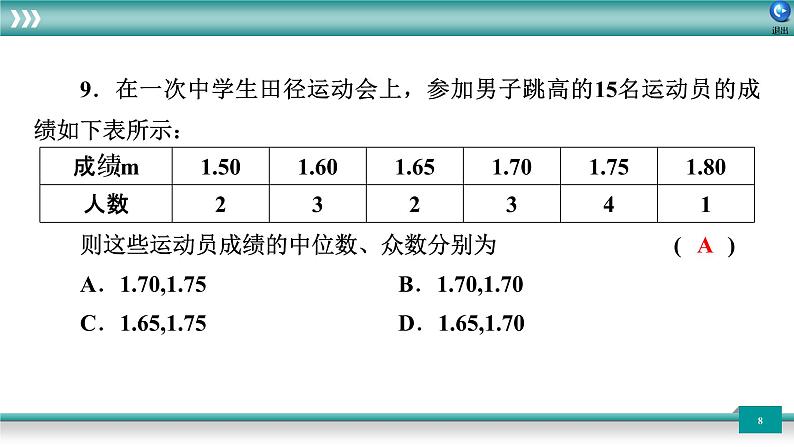
9．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：则这些运动员成绩的中位数、众数分别为(　　)A．1.70,1.75B．1.70,1.70　　C．1.65,1.75D．1.65,1.70
12．如图，△ABC为等腰直角三角形，∠ACB＝90°，AC＝BC＝2，正方形DEFG的边长也为2，且AC与DE在同一直线上，△ABC从C点与D点重合开始，沿直线DE向右平移，直到点A与点E重合为止，设CD的长为x，△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y，则y与x之间的函数关系的图象大致是(　　)
y(x＋1)(x－1)　
16．如图，扇形OAB是一个圆锥的侧面展开图，若小正方形网格的边长为1，则这个圆锥底面半径为______．
18．如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA，OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2020的纵坐标为_____________________．
三、解答题(本大题2小题，每小题12分，共24分)19．已知⊙O是△ABC的外接圆，CE为⊙O的直径，交AB于点F，连接AO并延长交BC于点D，AD⊥BC．
(1)证明：∵AD⊥BC，AD是过圆心的线段，∴BD＝CD．∴AB＝AC．∴∠BAD＝∠CAD．∵OA＝OC，∴∠OAC＝∠OCA．∵∠BFC＝∠FAC＋∠ACF，∴∠BFC＝3∠BAD．
20．如图1，一次函数的图象与两坐标轴分别交于A，B两点，且B点坐标为(0,4)，以A为顶点的抛物线解析式为y＝－(x＋2)2．(1)求一次函数的解析式；(2)如图2，将抛物线的顶点沿线段AB平移，此时抛物线顶点记为C，与y轴交点记为D，当点C的横坐标为－1时，求抛物线的解析式及D点的坐标；
(3)在(2)的条件下，线段AB上是否存在点P，使以B，D，P为顶点的三角形与△AOB相似？若存在，求出所有满足条件的P点坐标；若不存在，请说明理由．
(2)∵点C在直线y＝2x＋4上，且点C的横坐标为－1，∴y＝2×(－1)＋4＝2，∴点C坐标为(－1,2)．设平移后的抛物线解析式为y＝a(x－h)2＋k(a≠0)，∵a＝－1，顶点坐标为C(－1,2)，∴抛物线的解析式是y＝－(x＋1)2＋2．∵抛物线与y轴的交点为D，∴令x＝0，得y＝1，∴点D坐标为(0,1)．