初中数学8上2017-2018学年山东省菏泽市单县八年级上第一次月考数学试卷含解析练习含答案
展开2017-2018学年山东省菏泽市单县八年级(上)第一次月考数学试卷
一、选择题(本大题共12个小题,每小题3分,共36分)
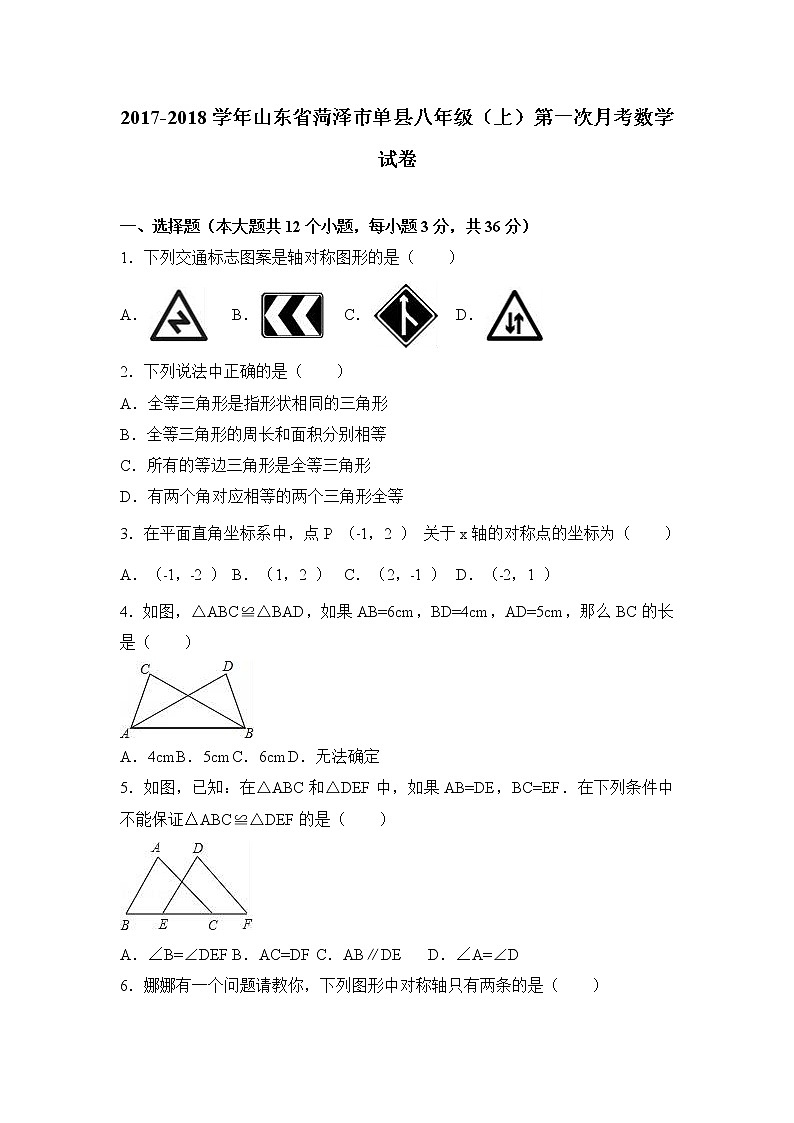
1.下列交通标志图案是轴对称图形的是( )
A. B. C. D.
2.下列说法中正确的是( )
A.全等三角形是指形状相同的三角形
B.全等三角形的周长和面积分别相等
C.所有的等边三角形是全等三角形
D.有两个角对应相等的两个三角形全等
3.在平面直角坐标系中,点P (﹣1,2 ) 关于x轴的对称点的坐标为( )
A.(﹣1,﹣2 ) B.(1,2 ) C.(2,﹣1 ) D.(﹣2,1 )
4.如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )
A.4cm B.5cm C.6cm D.无法确定
5.如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )
A.∠B=∠DEF B.AC=DF C.AB∥DE D.∠A=∠D
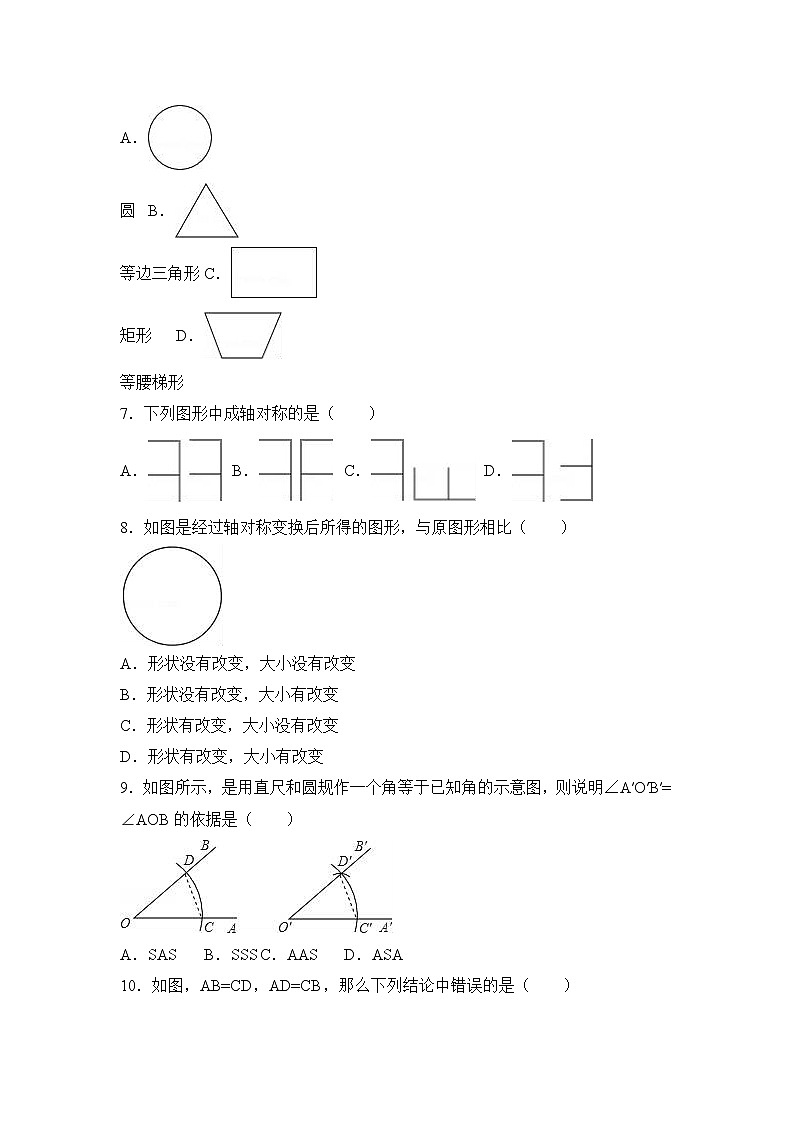
6.娜娜有一个问题请教你,下列图形中对称轴只有两条的是( )
A.
圆 B.
等边三角形 C.
矩形 D.
等腰梯形
7.下列图形中成轴对称的是( )
A. B. C. D.
8.如图是经过轴对称变换后所得的图形,与原图形相比( )
A.形状没有改变,大小没有改变
B.形状没有改变,大小有改变
C.形状有改变,大小没有改变
D.形状有改变,大小有改变
9.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
A.SAS B.SSS C.AAS D.ASA
10.如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD
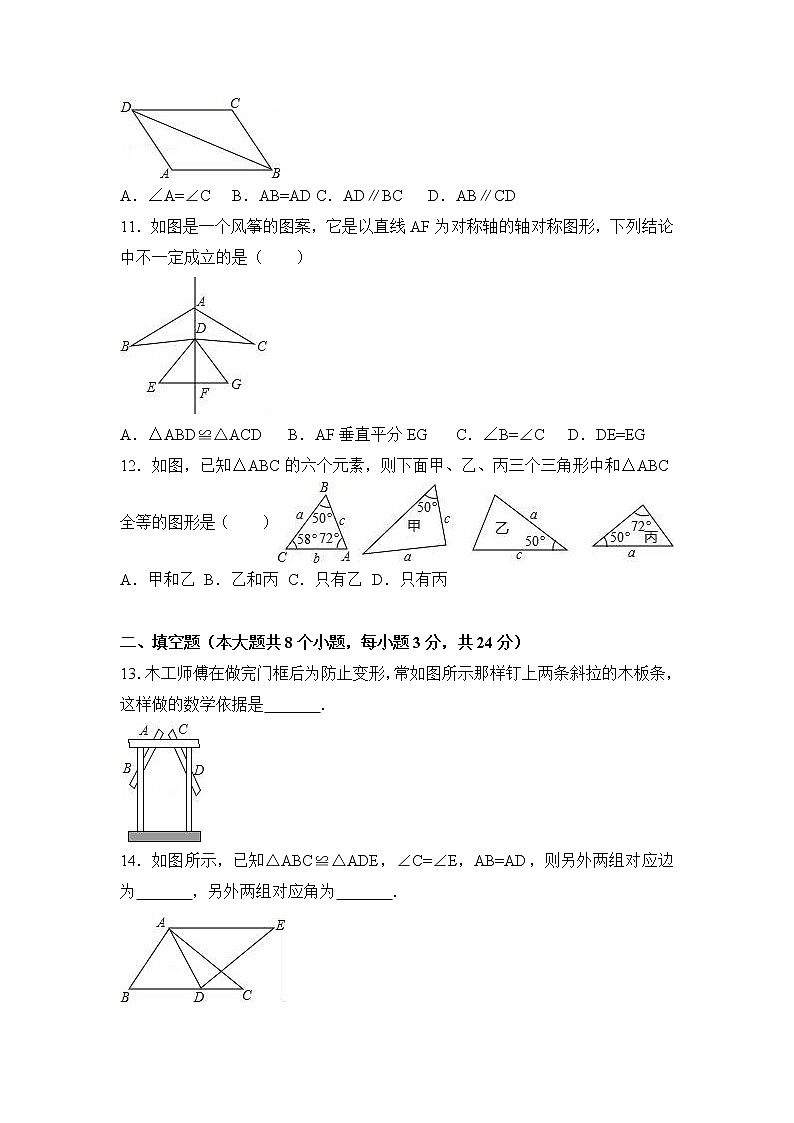
11.如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD B.AF垂直平分EG C.∠B=∠C D.DE=EG
12.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
二、填空题(本大题共8个小题,每小题3分,共24分)
13.木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是 .
14.如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为 ,另外两组对应角为 .
15.如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是 ,理由是 .
16.已知:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,AB=15cm,则∠C′= 度,A′B′= cm.
17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
18.已知△ABC≌△A′B′C′,若△ABC的面积为10cm2,则△A′B′C′的面积为 cm2;若△A′B′C′的周长为16cm,则△ABC的周长为 cm.
19.如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 (只添一个条件即可).
20.如图,点F、C在线段BE 上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还需补充一个条件 ,依据是 .
三、简答题
21.(8分)等腰三角形两边长为4cm、6cm,求等腰三角形的周长.
22.(8分)如图,AB=AC,AD=AE.求证:∠B=∠C.
23.(10分)如图,C是AB的中点,AD=CE,CD=BE.求证:△DCA≌△EBC.
24.(10分)已知AE、AD分别是△ABC的高和角平分线,且∠B=46°,∠C=60°,求∠DAE的度数.
25.(10分)如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明.
26.(14分)已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
2017-2018学年山东省菏泽市单县八年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题(本大题共12个小题,每小题3分,共36分)
1.(3分)下列交通标志图案是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称的定义结合选项所给的特点即可得出答案.
【解答】解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误;
故选:B.
【点评】本题考查了轴对称图形,掌握中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
2.(3分)下列说法中正确的是( )
A.全等三角形是指形状相同的三角形
B.全等三角形的周长和面积分别相等
C.所有的等边三角形是全等三角形
D.有两个角对应相等的两个三角形全等
【分析】根据能够完全重合的两个三角形叫做全等三角形,全等三角形的判定方法:AAS、AAS进行分析即可.
【解答】解:A、全等三角形是指形状相同的三角形,说法错误;
B、全等三角形的周长和面积分别相等,说法正确;
C、所有的等边三角形是全等三角形,说法错误;
D、有两个角对应相等的两个三角形全等,说法错误;
故选:B.
【点评】此题主要考查了全等三角形,关键是掌握全等三角形形状和大小都相等.
3.(3分)在平面直角坐标系中,点P (﹣1,2 ) 关于x轴的对称点的坐标为( )
A.(﹣1,﹣2 ) B.(1,2 ) C.(2,﹣1 ) D.(﹣2,1 )
【分析】根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
【解答】解:点P (﹣1,2 ) 关于x轴的对称点的坐标为(﹣1,﹣2),
故选:A.
【点评】本题考查了关于x轴对称的点的坐标,利用关于x轴对称的点的横坐标相等,纵坐标互为相反数是解题关键.
4.(3分)如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )
A.4cm B.5cm C.6cm D.无法确定
【分析】根据全等三角形的性质得出BC=AD,代入求出即可.
【解答】解:∵△ABC≌△BAD,AD=5cm,
∴BC=AD=5cm,
故选B.
【点评】本题考查了全等三角形的性质的应用,注意:全等三角形的对应边相等,对应角相等.
5.(3分)如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )
A.∠B=∠DEF B.AC=DF C.AB∥DE D.∠A=∠D
【分析】已知AB=DE,BC=EF,只需再找一个夹角或者一条边相等,即可判定△ABC≌△DEF.
【解答】解:A、可根据SAS判定△ABC≌△DEF,故本选项错误;
B、可根据SSS判定△ABC≌△DEF,故本选项错误;
C、根据AB∥DE,可得∠B=∠DEF,可根据SAS判定△ABC≌△DEF,故本选项错误;
D、不能根据SSA判定△ABC≌△DEF,故本选项正确.
故选D.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.(3分)娜娜有一个问题请教你,下列图形中对称轴只有两条的是( )
A.
圆 B.
等边三角形 C.
矩形 D.
等腰梯形
【分析】根据轴对称图形的概念,分别判断出四个图形的对称轴的条数即可.
【解答】解:A、圆有无数条对称轴,故本选项错误;
B、等边三角形有3条对称轴,故本选项错误;
C、矩形有2条对称轴,故本选项正确;
D、等腰梯形有1条对称轴,故本选项错误.
故选C.
【点评】本题考查轴对称图形的概念,解题关键是能够根据轴对称图形的概念正确找出各个图形的对称轴的条数,属于基础题.
7.(3分)下列图形中成轴对称的是( )
A. B. C. D.
【分析】根据轴对称图形的概念求解.
【解答】解:根据轴对称图形的概念可得:
是轴对称图形的是:B.
故选:B.
【点评】考查了轴对称图形,掌握好轴对称的概念.轴对称的关键是寻找对称轴,两边图象折叠后可重合.
8.(3分)如图是经过轴对称变换后所得的图形,与原图形相比( )
A.形状没有改变,大小没有改变
B.形状没有改变,大小有改变
C.形状有改变,大小没有改变
D.形状有改变,大小有改变
【分析】根据轴对称不改变图形的形状与大小解答.
【解答】解:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变.
故选:A.
【点评】本题考虑轴对称的性质,是基础题,熟记轴对称变换不改变图形的形状与大小是解题的关键.
9.(3分)如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
A.SAS B.SSS C.AAS D.ASA
【分析】由作法易得OD=O′D′,OC=O′C′,CD=C′D′,根据SSS可得到三角形全等.
【解答】解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',
故选:B.
【点评】本题主要考查了全等三角形的判定,关键是掌握全等三角形的判定定理.
10.(3分)如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD
【分析】根据题干给出的条件可以证明△ABD≌△CDB,可以求得A、C、D选项正确.
【解答】解:∵在△ABD和△CDB中,,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C
∴AD∥BC,AB∥CD,
∴A、C、D选项正确.
故选B.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABD≌△CDB是解题的关键.
11.(3分)如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD B.AF垂直平分EG C.∠B=∠C D.DE=EG
【分析】认真观察图形,根据轴对称图形的性质得选项A、B、C都是正确的,没有理由能够证明△DEG是等边三角形.
【解答】解:A、因为此图形是轴对称图形,正确;
B、对称轴垂直平分对应点连线,正确;
C、由三角形全等可知,∠B=∠C,正确;
D、题目中没有60°条件,不能判断是等边三角形,故不能得到DE=EG错误.
故选D.
【点评】本题考查了轴对称的性质;解决此题要注意,不要受图形误导,要找准各选项正误的具体原因是正确解答本题的关键.
12.(3分)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
【解答】解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选B.
【点评】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
二、填空题(本大题共8个小题,每小题3分,共24分)
13.(3分)木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是 三角形具有稳定性 .
【分析】根据三角形具有稳定性进行解答.
【解答】解:木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是三角形具有稳定性,
故答案为:三角形具有稳定性.
【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
14.(3分)如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为 AC=AE,BC=DE ,另外两组对应角为 ∠BAC=∠DAE,∠B=∠ADE .
【分析】由已知△ABC≌△ADE,∠C=∠E,AB=AD得C点与点E,点B与点D为对应点,然后根据全等三角形的性质可得答案.
【解答】解:∵△ABC≌△ADE,∠C=∠E,AB=AD,
∴AC=AE,BC=DE;
∴∠BAC=∠DAE,∠B=∠ADE.
【点评】本题考查了全等三角形的性质;找准对应关系是正确解答本题的关键.
15.(3分)如图所示,AE、BD相交于点C,要使△ABC≌△EDC,至少要添加的条件是 BC=DC或AC=EC ,理由是 两个三角形全等至少有一组对应边相等 .
【分析】要使△ABC≌△EDC,已知∠ACB=∠ECD,已知了一组对应角相等,因此至少添加一组对应边相等才可得出两三角形全等的结论.
【解答】解:要使△ABC≌△EDC,至少要添加的条件是BC=DC或AC=EC,
理由是两个三角形全等至少有一组对应边相等.
故答案为:BC=DC或AC=EC,两个三角形全等至少有一组对应边相等.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
16.(3分)已知:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,AB=15cm,则∠C′= 70 度,A′B′= 15 cm.
【分析】由已知条件,根据全等三角形有关性质即可求得答案.
【解答】解:∵△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,
∴∠C′与∠C是对应角,A′B′与边AB是对应边,
故填∠C′=70°,A′B′=15cm.
【点评】本题主要考查了全等三角形的性质,全等三角形的对应边相等,对应角相等,是需要熟记的内容.找准对应关系是正确解答本题的关键.
17.(3分)如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 4 对.
【分析】本题重点是根据已知条件“AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点”,得出△ABD≌△ACD,然后再由结论推出AB=AC,BE=DE,CF=DF,从而根据“SSS”或“SAS”找到更多的全等三角形,要由易到难,不重不漏.
【解答】解:∵AD⊥BC,AB=AC
∴D是BC中点
∴BD=DC,
∵AD=AD,
∴△ABD≌△ACD(SSS);
E、F分别是DB、DC的中点
∴BE=ED=DF=FC
∵AD⊥BC,AD=AD,ED=DF
∴△ADF≌△ADE(HL);
∵∠B=∠C,BE=FC,AB=AC
∴△ABE≌△ACF(SAS)
∵EC=BF,AB=AC,AE=AF
∴△ABF≌△ACE(SSS).
∴全等三角形共4对,分别是:△ABD≌△ACD(HL),△ABE≌△ACF(SAS),△ADF≌△ADE(SSS),△ABF≌△ACE(SAS).
故答案为4.
【点评】本题考查了全等三角形的判定.题目是一道考试常见题,易错点是漏掉△ABE≌△ACD,此类题可以先根据直观判断得出可能全等的所有三角形,然后从已知条件入手,分析推理,对结论一个个进行论证.其中△ABE≌△ACD常被忽略.
18.(3分)已知△ABC≌△A′B′C′,若△ABC的面积为10cm2,则△A′B′C′的面积为 10 cm2;若△A′B′C′的周长为16cm,则△ABC的周长为 16 cm.
【分析】根据全等三角形的面积相等,全等三角形的周长相等解答.
【解答】解:∵△ABC≌△A′B′C′,△ABC的面积为10cm2,
∴△A′B′C′的面积为10cm2;
∵△ABC≌△A′B′C′,△A′B′C′的周长为16cm,
∴△ABC的周长为16cm.
故答案为:10,16.
【点评】本题考查了全等三角形的性质,是基础题,需熟记.
19.(3分)如图,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是 CD=BD (只添一个条件即可).
【分析】由已知条件具备一角一边分别对应相等,还缺少一个条件,可添加DB=DC,利用SAS判定其全等.
【解答】解:需添加的一个条件是:CD=BD,
理由:∵∠1=∠2,
∴∠ADC=∠ADB,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
故答案为:CD=BD.
【点评】本题考查了三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.
20.(3分)如图,点F、C在线段BE 上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还需补充一个条件 AC=DF ,依据是 SAS .
【分析】要使△ABC≌△DEF,已知∠1=∠2,AC=EF,添加边的话应添加对应边,符合SAS来判定.
【解答】解:AC=DF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
故答案为:AC=DF,SAS.
【点评】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
三、简答题
21.(8分)等腰三角形两边长为4cm、6cm,求等腰三角形的周长.
【分析】两边的长为4m和6cm,具体哪边是底,哪边是腰没有明确,应分两种情况讨论
【解答】解:当腰长是4m,底长是6cm时,能构成三角形,则周长是:4+4+6=14cm;
当腰长是6m,底长是4cm时,能构成三角形,则周长是4+6+6=16cm;
则等腰三角形的周长是14cm或16cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
22.(8分)如图,AB=AC,AD=AE.求证:∠B=∠C.
【分析】欲证明∠B=∠C,只要证明△AEB≌△ADC.
【解答】证明:在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS)
∴∠B=∠C.
【点评】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.
23.(10分)如图,C是AB的中点,AD=CE,CD=BE.求证:△DCA≌△EBC.
【分析】根据中点定义可得AC=BC,再利用SSS判定△DCA≌△EBC即可.
【解答】证明:∵C是AB的中点,
∴AC=BC,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SSS).
【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
24.(10分)已知AE、AD分别是△ABC的高和角平分线,且∠B=46°,∠C=60°,求∠DAE的度数.
【分析】先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠DAC=∠BAC,而∠EAC=90°﹣∠C,然后利用∠DAE=∠DAC﹣∠EAC进行计算即可.
【解答】解:在△ABC中,∠B=46°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣46°﹣60°=74°,
∵AD是的角平分线,
∴∠DAC=∠BAC=37°,
∵AE是△ABC的高,
∴∠AEC=90°,
∴在△AEC中,∠EAC=180°﹣∠AEC﹣∠C=180°﹣90°﹣60°=30°,
∴∠DAE=∠DAC﹣∠EAC=37°﹣30°=7°.
【点评】考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的高线与角平分线的性质.
25.(10分)如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明.
【分析】连接AB,由题意知AC=DC,BD=EC,根据∠ACB=∠DCE即可证明△ABC≌△DEC,即可得AB=DE,即可解题.
【解答】解:连接AB,
由题意知:AC=DC,BC=EC,
在△ABC和△DEC中
∵,
∴△ABC≌△DEC(SAS),
∴DE=AB
故量出DE的长,就是A,B两点间的距离.
答:量出DE的长,就是A,B两点间的距离.
【点评】本题考查了全等三角形在实际生活中的应用,考查了全等三角形对应边相等的性质,本题中求证△ABC≌△DEC是解题的关键.
26.(14分)已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
【分析】根据角平分线上的点到角的两边距离相等可得PD=PE,利用“HL”证明Rt△OPD和Rt△OPE全等,根据全等三角形对应边相等可得OD=OE,再利用“边角边”证明△ODF和△OEF全等,然后利用全等三角形对应边相等证明即可.
【解答】证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,,
∴△ODF≌△OEF(SAS),
∴DF=EF.
【点评】本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,难点在于二次证明三角形全等.
2022-2023学年山东省菏泽市单县九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年山东省菏泽市单县九年级(上)期末数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
初中数学8下2017-2018学年山东省菏泽市定陶县八年级(上)期末数学试卷含答案含答案: 这是一份初中数学8下2017-2018学年山东省菏泽市定陶县八年级(上)期末数学试卷含答案含答案,共19页。试卷主要包含了精挑细选,火眼金睛,认真填写,试一试自己的身手,认真解答,一定要细心!等内容,欢迎下载使用。
初中数学8上2017-2018学年山东省菏泽市单县八年级上期末模拟数学试卷含答案解析练习含答案: 这是一份初中数学8上2017-2018学年山东省菏泽市单县八年级上期末模拟数学试卷含答案解析练习含答案,共16页。试卷主要包含了选择题,填空题,解答题,综合题等内容,欢迎下载使用。













