人教版八年级数学下册期末复习课件

这是一份人教版八年级数学下册期末复习课件，共60页。PPT课件主要包含了全章方法结构图，重点归类提升练，攻克陷阱提分练，超越自我拓展练，或225，AEGF，二四象限，图Z－19－1，≤m≤2等内容，欢迎下载使用。

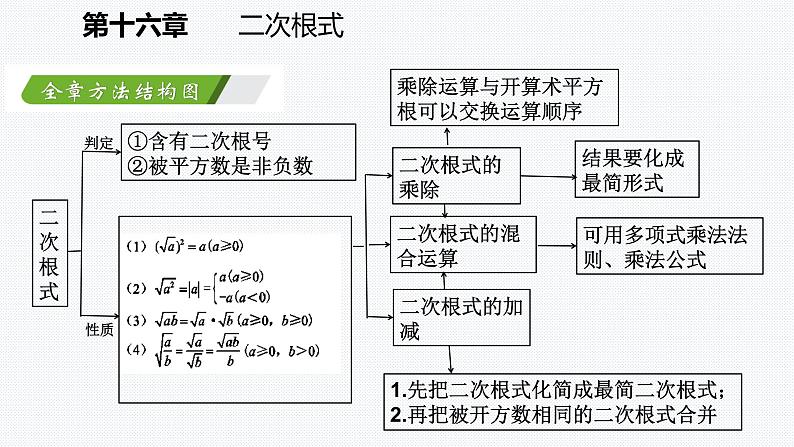
第十六章　 二次根式
二、二次根式计算的应用2．阅读与计算：请阅读以下材料，并完成相应的任务．斐波那契是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列(按照一定顺序排列着的一列数称为数列)．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．
第十七章 勾股定理
第十七章　 勾股定理
一、勾股定理的验证1．设直角三角形两直角边的长分别为a，b，斜边的长为c，作边长是(a＋b)的正方形ABCD，把正方形ABCD分成如图Z－17－1①所示的几部分，再把正方形ABCD分成如图②所示的几部分，请根据图①与图②，对勾股定理进行证明．
二、勾股定理的应用2．已知：如图Z－17－2，在△ABC中，D是BC的中点，DE⊥BC，垂足为D，交AB于点E，且BE 2－AE 2＝AC 2.(1)求证：∠A＝90°；(2)若AB＝8，AC＝4，求AE的长；(3)若DE＝3，BD＝4，求AE的长．
(2)∵AB＝8，CE＝BE，∴CE＋AE＝8，∴CE＝8－AE.在Rt△ACE中，AE 2＋AC 2 ＝CE 2，∴AE2＋42＝(8－AE)2，∴AE＝3.
3．如图Z－17－3，学校位于高速路AB的一侧(AB成一直线)，点A、点B为高速路上距学校直线距离最近的2个隧道出入口，点C、点D为学校的两幢教学楼．经测量，∠ACB＝90°，∠ADB＞90°，AC＝600 m，AB＝1000 m，D到高速路的最短直线距离DE＝400 m.
(1)求教学楼C到隧道出入口B的直线距离；(2)一辆载重汽车若从B沿BA方向驶向A，速度为70 km/h，该汽车经过时噪声影响的最远范围为距离汽车500 m，通过计算说明教学楼C和教学楼D是否会受到该汽车噪声的影响，如果受到影响，受到影响的时间分别是多少？(3)教学楼C和教学楼D分别到隧道出入口点A、点B直线距离的平方和谁大谁小？试计算比较说明(即比较图中AC2＋BC2与AD2＋BD2的大小)．
解：(1)在Rt△ABC中，∠C＝90°，根据勾股定理，得BC 2＝AB 2－AC 2＝10002－6002＝8002，∴BC＝800(m)，即教学楼C 到隧道出入口B的直线距离为800 m.(2)如图①，过点C作CF⊥AB于点F，
5．我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上的高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．●特例感知①等腰直角三角形___勾股高三角形(请填写“是”或“不是”)；②如图Z－17－5①，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高，若BD＝2AD＝2，试求线段CD的长．
●推广应用如图③，等腰三角形ABC为勾股高三角形，其中AB＝AC＞BC，CD为AB边上的高，过点D作BC边的平行线与AC边交于点E，若CE＝a，试求线段DE的长．
第十八章 平行四边形
第十八章　 平行四边形
(1)求证：四边形EBFD是平行四边形．(2)若∠ABC＝60°，BC＝2AB＝4，①求四边形EBFD的周长；②求证：CE是△AGD的中位线．(3)连接AC，BG，求证：∠BAC＝∠BGC.
(1)若AB＝4 cm，请解决下列问题：①点P运动几秒时，四边形PQBA是矩形？写出你的推理过程．②在点P运动的过程中，是否存在四边形PQCD是菱形的时刻？若存在，请求出运动的时间；若不存在，请说明理由．(2)当四边形PQBA是正方形时，求CD的长．
解：设运动时间为t s，则AP＝t，CQ＝3t，∴PD＝17－t，BQ＝20－3t.(1)①当AP＝BQ时，因为AD∥BC，∠B＝90°，所以四边形PQBA是矩形．此时t＝20－3t，∴t＝5，∴点P运动5 s时，四边形PQBA是矩形．
4．如图Z－18－4①，将△ABC纸片沿中位线EH折叠，使点A的对应点D落在BC边上，再将纸片分别沿等腰三角形BED和等腰三角形DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形．类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．
(1)将平行四边形ABCD纸片按图②的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段________，S矩形AEFG∶S平行四边形ABCD＝________．(2)平行四边形ABCD纸片还可以按图③的方式折叠成一个叠合矩形EFGH，若EF＝5，EH＝12，求AD的长；(3)如图④，四边形ABCD纸片满足AD∥BC，AD＜BC，AB⊥BC，AB＝8，CD＝10，小明把该纸片折叠，得到叠合正方形，请你帮助他画出叠合正方形的示意图，并求出AD，BC的长．
第十九章 一次函数
第十九章　 一次函数
1．已知函数y1＝(1－2m)x＋2m＋1，试解决下列问题：(1)当m＝2时，直线y1＝(1－2m)x＋2m＋1所在的象限是_______________；(2)m________时，y1是正比例函数；(3)m________时，y1随x的增大而增大；(4)m＝－2时，点A(a1，b1)，点B(a2，b2)在直线y1＝(1－2m)x＋2m＋1上，若b1>b2，则a1________a2(填“>”或“<”)；
(5)若直线y1＝(1－2m)x＋2m＋1与x轴的交点坐标为A(3，0)，与y轴的交点为B，求△ABO的面积；(6)试说明：直线y1＝(1－2m)x＋2m＋1必过点(1，2)；(7)若有点C(3，1)，D(6，1)，直线y1＝(1－2m)x＋2m＋1与线段CD(包括端点)有公共点，求m的取值范围；(8)已知点E(1，1)，F(5，6)，直线y2＝kx＋b经过点E，F，若直线y2由直线y1＝(1－2m)x＋2m＋1平移得到的，求m的值．
2.张老师计划到超市购买甲种文具100个，他到超市后发现还有乙种文具可供选择，其中甲种文具每个5元，乙种文具每个3元．如果调整文具购买品种，每减少购买1个甲种文具，需增加购买2个乙种文具．设购买x个甲种文具时，需购买y个乙种文具．(1)求y与x之间的函数关系式；(2)若张老师购买这两种文具共用去540元，则甲、乙两种文具各购买了多少个？
3．甲、乙两名运动员在一段2000米长的笔直公路上进行跑步比赛，比赛开始时甲在起点，乙在甲的前面200米处，他们同时同向出发匀速前进，甲的速度是8米/秒，乙的速度是6米/秒，先到终点者在终点原地等待．设甲、乙两人之间的距离是y米，比赛时间是x秒，当两人都到达终点计时结束，整个过程中y与x之间的函数图象是(　　)
4.已知直线y＝mx＋2m－4不经过第二象限，则m的取值范围是________．
(1)若点P在边AB，AD上，点P关于坐标轴的对称点Q落在直线y＝x－1上，求点P的坐标；(2)若点P在边AB，AD，CD上，G是AD与y轴的交点，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，求点P的坐标．
②当点P在边AB上时，设P(a，－4)，且1≤a≤7.若点P关于x轴的对称点Q2(a，4)在直线y＝x－1上，则4＝a－1，解得a＝5，此时P(5，－4)；若点P关于y轴的对称点Q4(－a，－4)在直线y＝x－1上，则－4＝－a－1，解得a＝3，此时P(3，－4)．综上所述，点P的坐标为(－3，4)或(－1，0)或(5，－4)或(3，－4)．
第二十章 数据的分析
第二十章　 数据的分析
1．某学校有两个校区：南校区和北校区，这两个校区九年级学生各有300名，为了解这两个校区九年级学生的英语单词掌握情况，进行了抽样调查，过程如下：①收集数据，从南校区和北校区的九年级学生中各随机抽取10名学生，进行英语单词测试，测试成绩(百分制)如下：
②整理、描述数据，按如下分数段整理、描述这两组样本数据：
(说明：90分及以上为优秀，80～89分为良好，60～79分为合格，60分以下为不合格)
③分析数据，对上述数据进行分析，分别求出了两组样本数据的平均数、中位数、众数、方差，如下表：
结合上述统计全过程，回答下列问题：(1)补全③中的表格；(2)请估计北校区九年级学生英语单词掌握情况为优秀的人数；(3)你认为哪个校区的九年级学生英语单词掌握得比较好？说明你的理由(至少从两个不同的角度说明推断的合理性)．
3．前南峪是河北省著名的红色旅游胜地，下表和统计图分别是前南峪景点一周的抽样统计参观人数和门票价格．
(1)把上表中一周的参观人数作为一个样本，直接指出这个样本的中位数是________，众数是________，平均数是________．(2)分析表中数据还可得到一些信息，如双休日参观人数远远高于平时等，请尝试再写出两条相关信息：①__________________________________；②__________________________________．
这一周每天参观人数不低于100人
一周内参观人数在100人左右的天数最多
(3)若五一期间有甲、乙两个旅游团到该景点参观，两团人数之和恰为上述样本数据的中位数，乙团人数不超过50，设两团分别购票共付W元，甲团人数为x.①求W关于x的函数关系式，并写出自变量的取值范围；②若甲团人数不超过100，则两团合起来购票比分开购票最多可节约多少钱？