
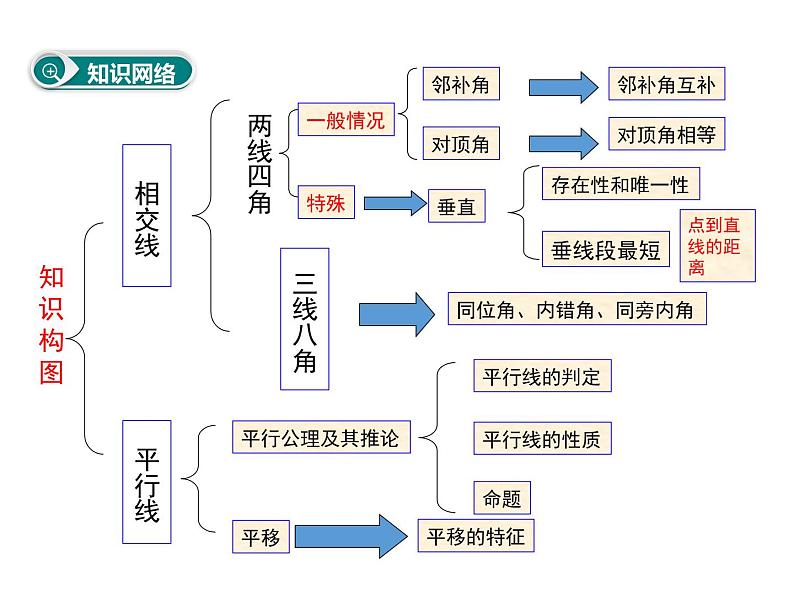


人教版七年级数学下册期末复习课件全套
展开同位角、内错角、同旁内角
【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
∵AB⊥CD,∴∠AOC=90°.∵∠AOE=65°,∴∠COE=25°又∵∠COE=∠DOF(对顶角相等)∴∠DOF=25°.
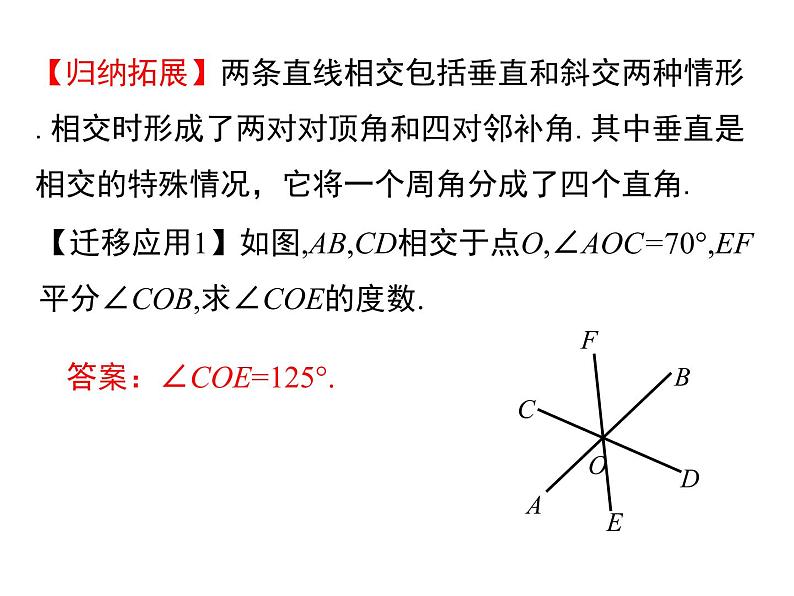
【迁移应用1】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.
答案:∠COE=125°.
【归纳拓展】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况,它将一个周角分成了四个直角.
【例2】如图,AD为三角形ABC的高,能表示点到直 线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条
解析:从图中可以看到共有三条,A到BC的垂线段AD,B到AD的垂线段BD,C到AD的垂线段CD.
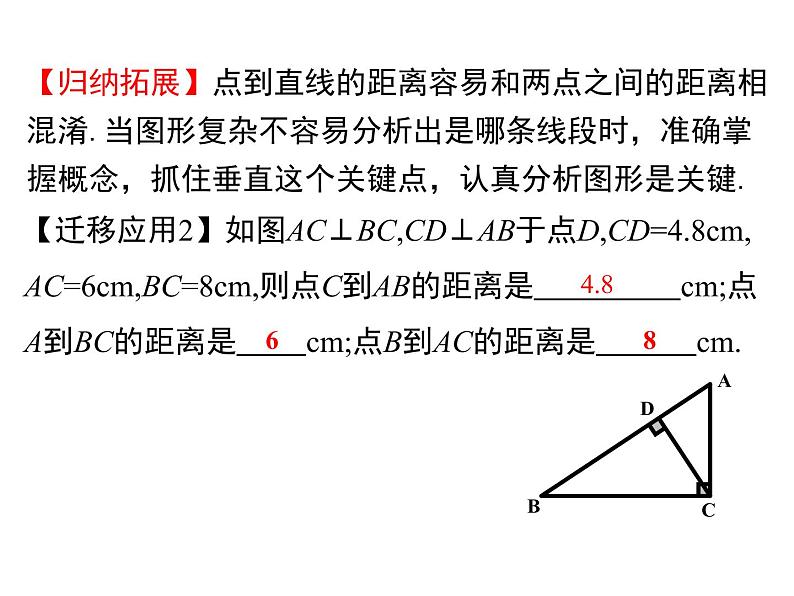
专题二 点到直线的距离
【迁移应用2】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.
【归纳拓展】点到直线的距离容易和两点之间的距离相混淆.当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键.
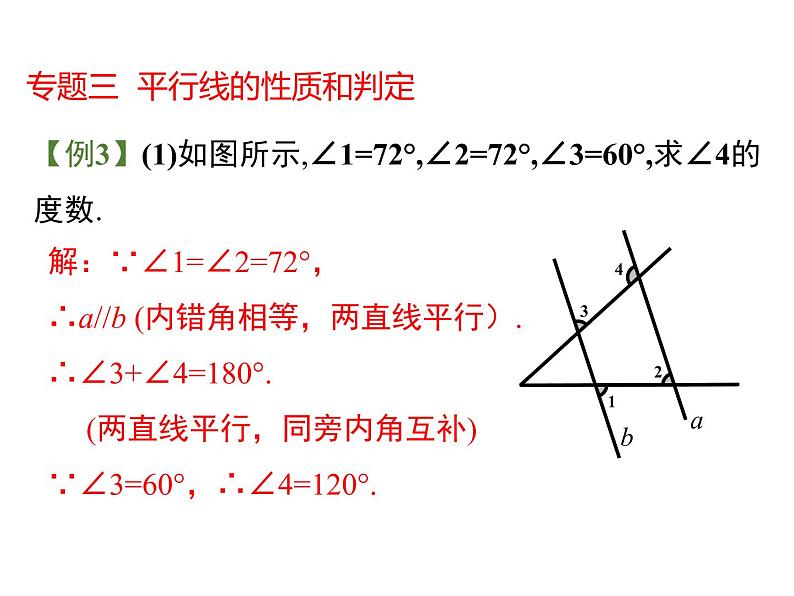
【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解:∵∠1=∠2=72°,∴a//b (内错角相等,两直线平行).∴∠3+∠4=180°. (两直线平行,同旁内角互补)∵∠3=60°,∴∠4=120°.
专题三 平行线的性质和判定
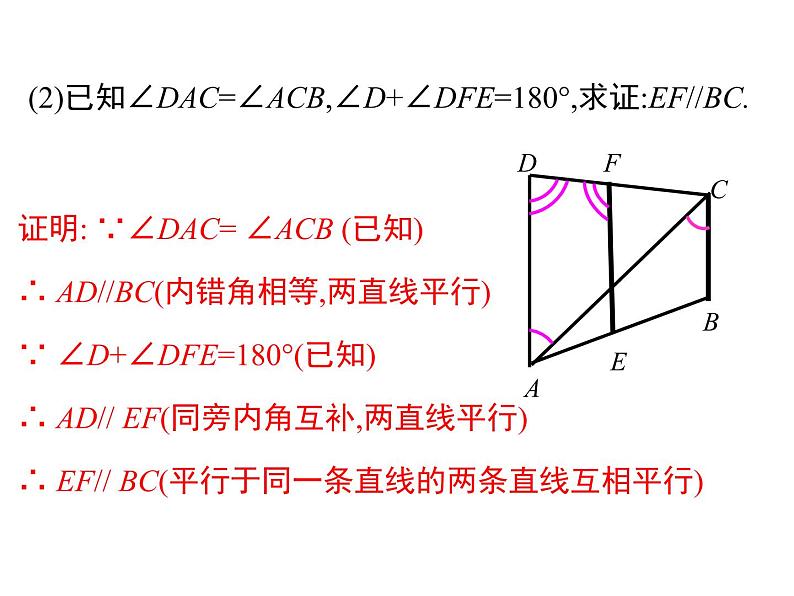
证明: ∵∠DAC= ∠ACB (已知)∴ AD//BC(内错角相等,两直线平行)∵ ∠D+∠DFE=180°(已知)∴ AD// EF(同旁内角互补,两直线平行)∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.
【迁移应用3】如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG的度数.
【归纳拓展】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.
【例4】如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是 ( )
解析:紧扣平移的概念解题.
【迁移应用4】如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是 ( )
【归纳拓展】平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等.
解:设∠1的度数为x°,则∠2的度数为x°,∠3的度数为8x°,根据题意可得x°+x°+8x°=180°,解得x=18.即∠1=∠2=18°,而∠4=∠1+∠2(对顶角相等).故∠4=36°.
专题五 相交线中的方程思想
【迁移应用5】如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
【归纳拓展】利用方程解决问题,是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.
请同学们总结一下本节课所复习的主要内容
若AB∥CD, 则∠ =∠ .
1.如图, 若∠3=∠4,则 ∥ ;
2.如图,∠D=70°,∠C= 110°,∠1=69°,则∠B= ·
3.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
4.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( ) A.75° B.45° C.30° D.15°
5. 如图,直线AB、CD相交于O,∠AOC=80°,∠1=30°; 求∠2的度数.
6. 如图,已知∠AEM=∠DGN,则你能说明AB平行于CD吗?
变式:若∠AEM=∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
七年级数学下(RJ) 教学课件
【例1】1.求下列各数的平方根:
2.求下列各数的立方根:
【归纳拓展】解题时,要注意题目的要求,是求平方根、立方根还是求算术平方根.
【迁移应用1】求下列各式的值:
A. 1个 B. 2个 C.3个 D.4个
【归纳拓展】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
专题二 实数的有关概念
【例3】(1) 位于整数 和 之间. (2)实数a,b在数轴上的位置如图所示,化简
= .
【归纳拓展】1.实数与数轴上的点是一一对应的关系;2.在数轴上表示的数,右边的数总是比左边的数大.
专题三 实数的估算及与数轴的结合
= .
【例4】(1) (2)
【例5】已知 , ,
,则 = , = .
【例6】计算: = .
【归纳拓展】开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
答案:(1)5.79;(2)5.48
1.通过对本章内容的复习,你认为平方根和立方根之 间有怎么样的区别与联系?
3.实数的运算法则与有理数的运算法则有什么联系?
1.写出两个大于1小于4的无理数____、____.
2. 的整数部分为____,小数部分为_ ____.
3.一个立方体的棱长是4cm,如果把它体积扩大为 原来的8倍,则扩大后的立方体的表面积是_______.
4.求下列各式中的x.
(1) (x-1)2=64; (2)
解:∵|3a+4|≥0且(4b-3)2≥0而|3a+4|+(4b-3)2=0∴|3a+4|=0且(4b-3)2=0∴a= ,b= .∴-ab=-( × )=1 , ∴ 1 的平方根是±1.
第七章 平面直角坐标系
点与有序数对的对应关系
坐标有序数对(x,y)
横坐标,右移加,左移减
纵坐标,上移加,下移减
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的 距离为5,则点a的值是 .
专题一 平面直角坐标系与点的坐标
【归纳拓展】1.第一、三象限内点的横、纵坐标同号;2.第二、四象限内点的横、纵坐标异号;3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的 距离是它横坐标的绝对值;4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线 上的点的横坐标相同.
【迁移应用1】(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则 m的值为 .
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则 点B的坐标是 .
(2,2)或(-2,2)
【例2】如图,把三角形ABC经过一定的变换得到三角形A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .
【归纳拓展】为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行了怎样的平移.
【迁移应用2】将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
【例3】(1)写出三角形ABC的各个顶点的坐标;(2)试求出三角形ABC的面积;(3)将三角形先向左平移5个单位长度,再向下平移4个单位长度,画出平移后的图形.
S=3×4-1/2×2×3-1/2×1×4 -1/2×1×3=5.5
专题三 平移作图及求坐标系中的几何图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转化为一些特殊的图形,去间接计算面积.(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
【迁移应用3】已知直角三角形ABC的直角边BC=AC,且B(3,2),C(3,-2),求点A的坐标及三角形ABC的面积.
解:∵B(3,2),C(3,-2), ∴BC∥y轴,且BC=2-(-2)=4, ∴AC=BC=4. ∴三角形ABC面积是1/2×4×4=8. ∵AC⊥BC,∴AC⊥y轴, ∴点A的横坐标为3-4=-1,纵坐标为-2, ∴A点坐标为(-1,-2).
坐标系画法(坐标、x轴和y轴、象限)
表示地理位置(选、建、标、写)
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的 坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标 是 .
3.点A(2,3)到x轴的距离为 ;点B(-4,0)到y 轴的距离为 ;点C到x轴的距离为1,到y轴的 距离为3,且在第三象限,则C点坐标是 .
4.直角坐标系中,在y轴上有一点P ,且OP=5,则 P的坐标为 .
(0 ,5)或(0 ,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
第八章 二元一次方程组
数学问题的解(二元或三元一次方程组的解)
数学问题(二元或三元一次方程组)
实际问题的答案
【例1】若x2m-1+5y3n-2m=7是二元一次方程,则m= , n= .
由二元一次方程的定义可得:
专题一 二元一次方程与二元一次方程组
【迁移应用1】已知方程(m-3) +(n+2) =0是关于x、y的二元一次方程,求m、n的值.
解:由题可得:|n| -1=1,m≠3,m2-8=1,n ≠-2. 解得:m=-3,n=2.
【归纳拓展】首先理解二元一次方程或二元一次方程组定义的几大因素,并且通过定义得到需要的等式,由等式得到最后的求解.
把x=1,y=-2代入二元一次方程组得
解得:a=-1,b=1.5.
专题二 二元一次方程与二元一次方程组的解
【归纳拓展】一般情况下,提到二元一次方程(组)的解,须先把解代入二元一次方程(组),得到解题需要的关系式,然后解关系式,即可解决问题.
【迁移应用2】已知x=1,y=-2满足(ax-2y-3)2+ |x-by+4 |=0,求a+b的值.
解:由题意可得: 把x=1,y=-2代入方程组 可得: 解得:a=-1,b=-2.5,则a+b=-3.5.
由①可得y=3x-7 , ③
将③代入②得 5x+2(3x-7)=8,
解得x=2,把x=2代入③得
由此可得二元一次方程组的解是
专题三 代入消元法与加减消元法
【例4】用加减消元法解方程组
由②-①得 18=y+11,解得y=7,
把y=7代入①得 3x=28-16+3,
由此可得二元一次方程组的解为
【归纳拓展】①代入消元法是将其中的一个方程写成“y=”或“x=”的形式,并把它代入另一个方程,得到一个关于x或y的一元一次方程求得x或y值.②加减消元法是通过两个方程两边相加(或相减)消去一个未知数,把二元一次方程组转化为一元一次方程.
【迁移应用3】 已知-4xm+nym-n与-2x7-my1+n是同类项,求m,n的值.
【迁移应用4】 已知方程组 的解为 则求6a-3b的值.
解:将 代入原方程组得 解得 所以6a-3b=6×3-3×1=15.
【例5】某汽车运输队要在规定的天数内运完一批货物,如果减少6辆汽车则要再运3天才能完成任务;如果增加4辆汽车,则可提前一天完成任务,那么这个汽车运输队原有汽车多少辆?原规定运输的天数是多少?
分析:等量关系式: ①减少6辆汽车后运输的货物=原规定运输货物; ②增加4辆汽车后运输的货物=原规定的货物。
专题四 二元一次方程组的实际应用
解:设这个汽车运输队原有汽车x辆,原规定完成的天数为y天,每辆汽车每天的运输量为1.
根据题意可得 化简整理得:
由②可得x=4y-4 ,③
3(4y-4)-6y=18,
答:原有汽车16辆,原规定完成的天数为5天.
【归纳拓展】利用方程的思想解决实际问题时,1.首先要找准等量关系式,找等量关系式时要注意题干 中提到的等量关系的语句,2.根据等量关系列得方程, 主要步骤是“找”“设”“列”“解”“答”,一步 都不能少.
解:设该年级寄宿学生有x人,宿舍有y间.根据题意可得 解得
答:设该年级寄宿学生有514人,宿舍有85间.
【迁移应用5】某校七年级安排宿舍,若每间宿舍住6人,则有4人住不下,若每间住7人,则有1间只住3人,且空余11间宿舍,求该年级寄宿学生有多少人?宿舍有多少间?
1.二元一次方程(组)的定义及解的定义
2.二元一次方程组的解法
3.二元一次方程组的应用
4.方程组 中,x与y的和为12,求k的值.
5.A、B两地相距36千米.甲从A地出发步行到B地,乙从B地出发步行到A地.两人同时出发,4小时相遇,6小时后,甲所余路程为乙所余路程的2倍,求两人的速度.
解:设甲、乙的速度分别为x千米/时和y千米/时.
答:甲、乙的速度分别为4千米/时和5千米/时.
第九章 不等式与不等式组
数学问题的解(不等式(组)的解集)
实际问题(包含不等关系)
数学问题 (一元一次不等式(组))
专题一 一元一次不等式的定义和性质
【归纳拓展】一元一次不等式的概念含几个要点:(1)用不等号连接;(2)不等号两边都是关于未知数的整式;(3)只含有一个未知数,且含有未知数的项的最高 次数为1.
(1)x<6,数轴上表示为
(2)y<2,数轴上表示为
专题二 解一元一次不等式
【归纳拓展】解不等式一定要把握好基础知识:①不等式的性质;②去分母,去括号,合并同类项.熟练掌握并利用这些基础知识解题,保证准确率.
【迁移应用2】不等式4x-6 ≥7x-12的非负整数解为 .
【例3】小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
【分析】从路程下手找不等关系:即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
专题三 一元一次不等式的应用
【归纳拓展】不等式的应用情况很多,但解所有的题目关键在于找准表示不等关系的语句,并能够列出不等式,再利用不等式的性质解不等式,这样问题才能得以解决.
提示:解不等式x-a≥0,得x≥a;解不等式-2x>-4,得x<2.因为不等式组有解,故2在a的右边,即a<2.
专题四 一元一次不等式组的定义与解集
【归纳拓展】不等式组的解集确定方法除利用数轴直观确定外,还可以用口诀确定:同大取大,同小取小,大小小大中间找,大大小小没得找.
解:①不等式组的解集是 ;
②不等式组的解集是x≥9.
专题五 解一元一次不等式组
【归纳拓展】解不等式组的基础是解不等式,把每个不等式的解集解出来后,按求不等式组解集的口诀或利用画数轴的方法找到解集.
提示:不等式组的解集是1
【例6】一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
设小朋友总共有x人,由此可得不等式组
由此可得5
【归纳拓展】当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属于通过列不等式(组)来解决的问题,而不属于通过列方程(组)来解决的问题.
1.一元一次不等式的定义和性质
2.一元一次不等式的解法及应用
3.一元一次不等式组的定义、解集及应用
1.已知点M(3a-9,1-a)在第三象限,且它的横、纵坐标都 是整数,则a的值是( ) A. 1 B. 2 C. 3 D. 0
2.关于x的不等式x-2a≤1的解集如图所示,则a的值是 .
解:1
【应用迁移1】为了了解某县初中二年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法中正确的是( )A.9800名学生是总体 B.每个学生是个体C.100名学生是所抽取的一个样本D.样本容量是100
【归纳拓展】抽样调查的考察内容较广,所以打好基础,全面掌握有关抽样调查的知识,抓住知识的要点,灵活运用知识进行判断.
专题二 统计图及其应用
【例2】小明把自己一周的支出情况,用如图所示的统计图来表示,下面说法正确的是 ( )
A.可以直接看出具体消费数额
B.可以直接看出总消费额
C.可以直接看出各项消费额占总消费额的百分比
D.可以直接看出各项消费额在一周中的具体变化情况
【归纳拓展】我们只有掌握好各种统计图的特点以后,才能更好地解决这类问题.所以本章没有难题,只要把基础打扎实了,大部分题目都是比较简单的.
【迁移应用2】新华中学制作了有关300名学生选择棋类、武术、摄影、刺绣四门校本课程情况的扇形统计图,从图中可以看出选择刺绣的学生为 人.
【例3】对某班学生一次数学测验成绩(成绩为正数)进行各分数段人数的统计如图所示,根据图示信息填空: (1)该班有学生 人;(2)成绩在69.5~79.5范围内的人数为 .(3)如果以大于或等于80分为优良,那么该班的优良率约为 .
专题三 频数分布直方图及其应用
【归纳拓展】学会从图形中获取信息,然后利用所得信息结合已知解决问题,其中要注意结合统计图的特点.
【应用迁移3】 为进一步加强中小学生近视眼的防控,市教育局近期下发了有关文件,将学生视力保护工作纳入学校和教师的考核内容,为此,某县教育主管部门对今年初中毕业生的视力进行了一次抽样调查,并根据调查结果绘制如下频数分布表和频数分布直方图的一部分.
解:(1)这次调查的人数是:15 ÷0.05=300 (人), 所以a=300 ×0.25=75 ,b=60 ÷300=0.2 , 因为a=75 ,所以4.9 ~5.1 范围内的人数是75 .图略.
(2)若视力在4.9 以上(含4.9 )均属正常,估计该县5600 名初中毕业生视力正常的学生有多少人?
(2)根据题意得:5600 ×(0.25+0.2 )=2520 (人). 答:该县初中毕业生视力正常的学生有2520 人.
专题四 统计图的综合应用
【例3】某学校为了了解学生课外参加体育锻炼的情况,随机抽取了该校七、八、九年级共1600名学生进行抽样调查,发现只有25%的学生课外参加体育锻炼,整理收集到的数据,绘制成如图所示的统计图.根据以上信息,解答下列问题:
(1)九年级共抽查了 名学生,其圆心角为 ; (2)九年级学生课外参加体育锻炼的占九年级人数 比例为 ;
解析:被抽查的学生中,参加体育锻炼的人数为 40+20+15=75(人),故被调查的学生人数为75÷25%=300(人),故九年级被调查的学生有300×(1-40%-30%)=90(人),所以九年级部分所对的扇形圆心角为360°×30%=108°,九年级学生参加体育锻炼的占九年级人数的比例为
(3)若该校七、八、九年级分别有600人、500人、500人,按各年级参加体育锻炼的比例计算,则全校学生中课外参加体育锻炼的约有多少人?
解:全校学生中课外参加体育锻炼的人数为
1.各统计图的识图方法、特点和画法
2.全面调查和抽样调查的特点及选用
3.抽样调查的有关概念
4.统计图的信息的获取和应用
1.下列调查工作需采用全面调查方式的是( )A.环保部门对淮河某段水域的水污染情况的调查B.电视台对正在播出的某电视节目收视率的调查C.质检部门对各厂家生产的电池使用寿命的调查D.企业在给职工做工作服前进行的尺寸大小的调查
2.要反映某市一周内每天的最高气温的变化情况,宜 采用( ) A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
3.某住宅小区6月份随机抽查了该小区6天的用水量(单位:t),结果分别是30,34,32,37,28,31,那么请你估计该小区6月份的总用水量约是( )A.940 B.950 C.960 D.980
4.某市为了了解七年级学生的身体素质情况,随机抽取了500名七年级学生进行检测,身体素质达标率为92%.请你估计该市6万名七年级学生中,身体素质达标的大约有 万人.
5.七年级某次抽考的各学科满分值情况如下表,若把本次七年级抽考各科满分值比例绘成扇形统计图,则数学所在的圆心角是 度.
6.某地区教育部门要了解初中学生阅读课外书籍的情况,随机调查了本地区500名初中学生一学期阅读课外书的本数,并绘制了如图的统计图.请根据统计图反映的信息回答问题.
七年级数学上册期末复习-(人教版)课件PPT: 这是一份七年级数学上册期末复习-(人教版)课件PPT,共60页。
七年级数学下册期末复习课件-(北师大): 这是一份七年级数学下册期末复习课件-(北师大),共31页。PPT课件主要包含了-20a3b3,nn-1,a+8b,y=21x,y=2x+1等内容,欢迎下载使用。
七年级数学下册期末复习-(北师大)课件PPT: 这是一份七年级数学下册期末复习-(北师大)课件PPT,共17页。












