2021-2022学年吉林省长春十一高中北湖学校七年级（下）期末数学试卷（Word解析版）

2021-2022学年吉林省长春十一高中北湖学校七年级（下）期末数学试卷

一、选择题（本题共8小题，共24分）

1. 北京冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是(    )

A.  B.  C.  D.

2. 下列各式中是一元一次方程的是(    )

A.  B.  C.  D.

3. 已知，下列不等式不一定成立的是(    )

A.  B.
C.  D.

4. 学校购买一种正多边形形状的瓷砖来铺满教室的地面，所购买的瓷砖形状不可能是(    )

A. 等边三角形 B. 正五边形 C. 正六边形 D. 正方形

5. 现有两根长度分别这和的木棒，若要钉成一个三角形木棒，则第三根木棒长可以为(    )

A.  B.  C.  D.

6. 九章算术中记载：“今有上禾三秉，益实六斗，当下禾十秉；下禾五秉，益实一斗，当上禾二秉．问上、下禾实一秉各几何？”其大意是：今有上等稻子三捆，若打出来的谷子再加六斗，则相当于十捆下等稻子打出来的谷子；有下等稻子五捆，若打出来的谷子再加一斗，则相当于两捆上等稻子打岀来的谷子．问上等、下等稻子每捆打多少斗谷子？设上等稻子每捆打斗谷子，下等稻子每捆打斗谷子，根据题意可列方程组为(    )

A.  B.
C.  D.

7. 如图，将绕顶点逆时针旋转到，，，则的度数为(    )

A.
B.
C.
D.

8. 关于的不等式的解集为，那么的取值范围是(    )

A.  B.  C.  D.

二、填空题（本题共6小题，共18分）

9. 已知方程，用含的代数式表示，则______．
10. 如图，已知为等边三角形，若沿图中虚线剪去，则______．

11. 如图，沿方向平移得到若，，则的长是______．

12. 在三角形的三边关系一节中“三角形的任何两边的和大于第三边”，这一结论的根本依据是______．
13. 如图，在中，已知点，，分别为边，，的中点，且，则_______．

14. 不等式组只有两个整数解，则的取值范围是______．

三、选择题（本题共10小题，共78分）

15. 解下列方程：
    ．
    ．
16. 解二元一次方程组．
17. 解不等式组，并把它的解集在数轴上表示出来．
     
18. 已知一个多边形的内角和比外角和大，求这个多边形的边数．
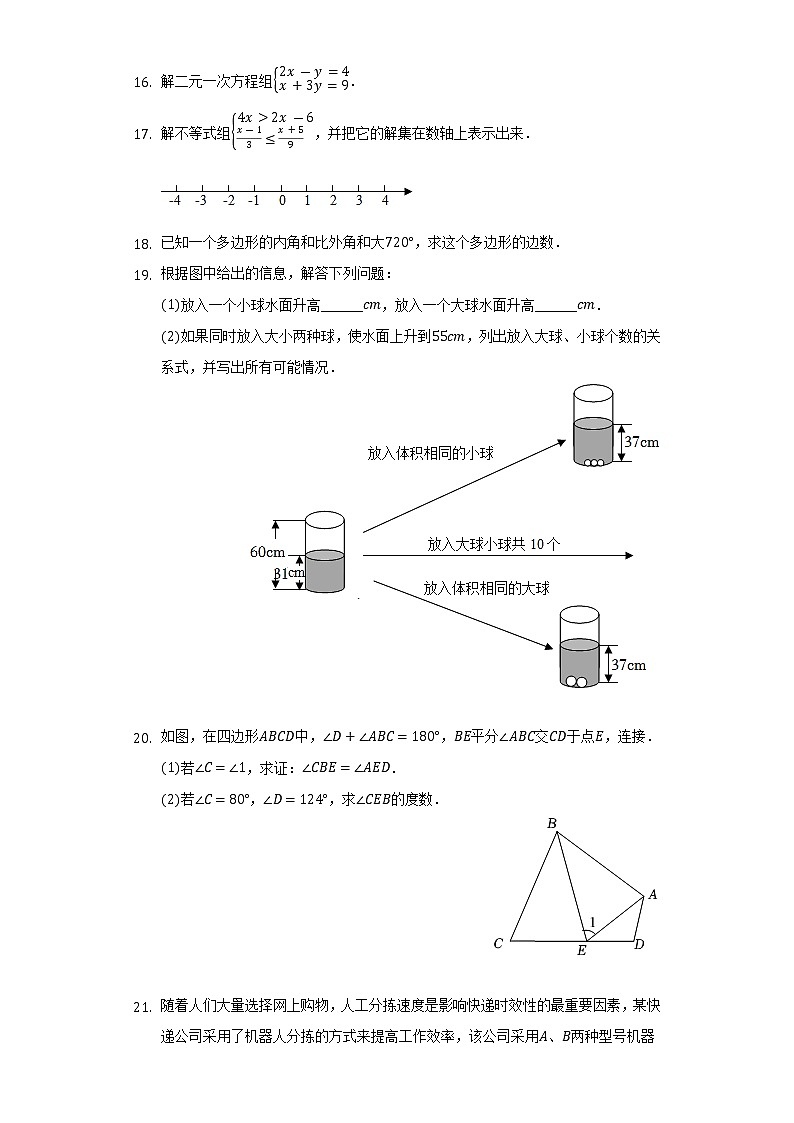
19. 根据图中给出的信息，解答下列问题：
    放入一个小球水面升高______，放入一个大球水面升高______．
    如果同时放入大小两种球，使水面上升到，列出放入大球、小球个数的关系式，并写出所有可能情况．

20. 如图，在四边形中，，平分交于点，连接．
    若，求证：．
    若，，求的度数．

21. 随着人们大量选择网上购物，人工分拣速度是影响快递时效性的最重要因素，某快递公司采用了机器人分拣的方式来提高工作效率，该公司采用、两种型号机器人，若型机器人工作小时，型机器人工作小时，一共可以分拣件包裹；若型机器人工作小时，型机器人工作小时，一共可以分拣件包裹．
    求型、型两个机器人每小时各分拣多少件包裹．
    “”期间，快递公司的业务量猛增，要让型、型机器人每天分拣包裹的总量不低于件，它们每天至少要一起工作多少小时？
22. 如图，每个小方格都是边长为个单位长度的小正方形．
    将向右平移个单位长度，画出平移后的．
    画出关于直线成轴对称的．
    作出，并且过点画出一条直线将的面积分成相等的两部分．
    在直线上找一点，使最短，保留作图痕迹．

23. 阅读下列解方程组的方法，然后解答问题：
    解方程组时，小明发现如果用常规的代入消元法、加减消元法来解，计算量大，且易出现运算错误，他采用下面的解法则比较简单：
    得：，即
    得：
    得：，代入得．
    所以这个方程组的解是．
    请你运用小明的方法解方程组．
    规律探究：猜想关于，的方程组，的解是______．
24. 如图，在中，，，将绕着的中点旋转得到，点为的中点．点从点出发沿折线的方向以每秒的速度向终点运动，连结，设点的运动时间为秒．
    ______，______度．
    用含的代数式表示的长．
    当将四边形的周长分成：两部分时，求的值．
    在点的运动过程中，作点关于直线的对称点，连结，当与四边形的边垂直时，请直接写出的度数．

答案和解析

1.【答案】 

【解析】解：不是中心对称图形，也不是轴对称图形，故此选项不合题意；
B.不是中心对称图形，也不是轴对称图形，故此选项不合题意；
C.既是中心对称图形，也是轴对称图形，故此选项符合题意；
D.不是中心对称图形，也不是轴对称图形，故此选项不合题意；
故选：．
根据中心对称图形与轴对称图形的概念进行判断即可．
本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转度后与自身重合．
 

2.【答案】 

【解析】解：根据一元一次方程的定义，中有两个未知数，那么不是一元一次方程，故A不符合题意．
B.根据一元一次方程的定义，是一元一次方程，故B符合题意．
C.根据分式方程的定义，是分式方程，故C不符合题意．
D.根据一元一次方程的定义，中未知数的最高次数是，那么不是一元一次方程，故D不符合题意．
故选：．
根据一元一次方程的定义解决此题．
本题主要考查一元一次方程，熟练掌握一元一次方程的定义是解决本题的关键．
 

3.【答案】 

【解析】解：，
，故本选项不合题意；
B.，
，故本选项不合题意；
C.，
，
，故本选项不合题意；
D.，当时，，所以原式不一定成立，故本选项符合题意；
故选：．
直接利用不等式的基本性质分别分析得出答案．
本题考查了不等式的性质，掌握不等式的两边同时加上或减去同一个数或同一个含有字母的式子，不等号的方向不变；不等式的两边同时乘或除以同一个正数，不等号的方向不变；不等式的两边同时乘或除以同一个负数，不等号的方向改变是解题的关键．
 

4.【答案】 

【解析】解：、等边三角形的每个内角是，能整除，能密铺；
B、正五边形的每个内角为：，不能整除，不能密铺；
C、正六边形的每个内角是，能整除，能密铺；
D、正方形的每个内角是，个能密铺．
故选：．
根据一种正多边形的镶嵌应符合一个内角度数能整除，进而判断得出即可．
本题主要考查了平面镶嵌，由平面镶嵌的知识可知只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形．
 

5.【答案】 

【解析】解：设第三根木棒长为，
则，即，
四个选项中，第三根木棒长可以为，
故选：．
根据三角形的三边关系确定第三边的范围，判断即可．
本题考查的是三角形的三边关系，熟记三角形两边之和大于第三边、两边差小于第三边是解题的关键．
 

6.【答案】 

【解析】解：设上等稻子每捆打斗谷子，下等稻子每捆打斗谷子，
根据题意可列方程组为：．
故选：．
设上等稻子每捆打斗谷子，下等稻子每捆打斗谷子，分别利用已知“今有上等稻子三捆十捆下等稻子打出来的谷子；有下等稻子五捆两捆上等稻子打岀来的谷子“分别得出等量关系求出答案．
此题主要考查了由实际问题抽象出二元一次方程组，正确得出等量关系是解题关键．
 

7.【答案】 

【解析】解：将绕顶点逆时针旋转到，，
，，
，
，
，
故选：．
由旋转的性质及，得出，，由，求出，再根据三角形内角和定理即可求出的度数．
本题考查了旋转的性质，掌握旋转的性质，三角形内角和定理是解决问题的关键．
 

8.【答案】 

【解析】解：关于的不等式的解集为，
，
解得，
故选：．
根据不等式的解集为，知，解之即可．
本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
 

9.【答案】 

【解析】解：，
，
，
故答案为：．
把看作已知数求出即可．
此题考查了解二元一次方程，解题的关键是将看作已知数求出．
 

10.【答案】 

【解析】解：为等边三角形，
，
，，
，
，
，
故答案为：．
根据等边三角形的性质可得，根据三角形外角的性质以及三角形内角和定理可得的度数．
本题考查了等边三角形的性质，三角形外角的性质，三角形的内角和定理等，熟练掌握这些知识是解题的关键．
 

11.【答案】 

【解析】解：沿方向平移得到，
，
，
，
，
故答案为：．
根据沿方向平移得到求出，从而可求出，即可求得．
本题考查平移的性质，解题的关键是根据平移的性质求出．
 

12.【答案】两点之间，线段最短 

【解析】解：在三角形的三边关系一节中“三角形的任何两边的和大于第三边”，这一结论的根本依据是两点之间，线段最短．
故答案为：两点之间，线段最短．
根据线段的性质即可求解．
本题考查了三角形三边关系定理的推导，掌握线段的性质是解题的关键．
 

13.【答案】 

【解析】

【分析】
根据三角形的面积公式，知的面积是的面积的一半，进一步求得阴影部分的面积是的面积的一半．
此题主要是根据三角形的面积公式知三角形的中线把三角形的面积分成相等的两部分．
【解答】
解：点是的中点，
的面积是的面积的一半，的面积是的面积的一半．
则的面积是的面积的一半，即为．
点是的中点，
阴影部分的面积是的面积的一半，即为．
故答案为．  

14.【答案】 

【解析】解：不等式组整理得：，
不等式组只有两个整数解，
，整数解为，，
则的取值范围是．
故答案为：．
不等式组整理后，根据只有两个整数解，确定出的范围即可．
此题考查了一元一次不等式组的整数解，熟练掌握不等式组的解法是解本题的关键．
 

15.【答案】解：，
，
，
，
；
，
，
，
，
，
． 

【解析】去括号、移项、合并同类项、系数化为，即可求解；
去分母、去括号、移项、合并同类项、系数化为，即可求解．
本题考查解一元一次方程，熟练掌握解一元一次方程的方法，准确计算是解题的关键．
 

16.【答案】解：
由得
把代入得，
，
解得，
把代入得，
原方程组的解为． 

【解析】由第个方程可得用表示的的式子，代入第个方程可得的值，进而可得的值．
考查解二元一次方程组；当一个方程中未知数的系数为时，可考虑用代入法求解比较简便．
 

17.【答案】解：解不等式，得：，
解不等式，得：，
不等式组的解集是，
在数轴上表示为：
 

【解析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．
本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
 

18.【答案】解：设这个多边形的边数是，
则，
解得．
故它的边数为． 

【解析】根据多边形的内角和公式与外角和定理列式求解即可．
本题考查了多边形的内角和与外角和定理，熟记多边形的外角和都是是解题的关键．
 

19.【答案】   

【解析】解：

；


．
故答案为：；．
设放入个小球，个大球，
依题意得：，
，
又，均为正整数，
或或，
共有种放入方式，
方案：放入个小球，个大球；
方案：放入个小球，个大球；
方案：放入个小球，个大球．
根据放入球的数量及水面升高的高度，即可求出放入一个小球或放入一个大球水面升高的高度；
设放入个小球，个大球，根据水面升高的总高度为，即可得出关于，的二元一次方程，再结合，均为正整数，即可得出各放入方式．
本题考查了二元一次方程的应用，找准等量关系，正确列出二元一次方程是解题的关键．
 

20.【答案】证明：，，，
；
解：，，
，
平分，
，
，，
． 

【解析】根据三角形内角和定理及平角的定义求解即可；
根据三角形内角和定理及角平分线的定义求解即可．
此题考查了三角形内角和定理，熟记三角形内角和定理是解题的关键．
 

21.【答案】解：设型机器人每小时分拣件包裹，型机器人每小时分拣件包裹，
由题意得：，
解得：，
答：型机器人每小时分拣件包裹，型机器人每小时分拣件包裹；
设型、型机器人每天要一起工作小时，
由题意得：，
解得：，
答：型、型机器人每天至少要一起工作小时． 

【解析】设型机器人每小时分拣件包裹，型机器人每小时分拣件包裹，由题意：若型机器人工作小时，型机器人工作小时，一共可以分拣件包裹；若型机器人工作小时，型机器人工作小时，一共可以分拣件包裹．列出二元一次方程组，解方程组即可；
设型、型机器人每天要一起工作小时，由题意：让型、型机器人每天分拣包裹的总量不低于件，列出一元一次不等式，解不等式即可．
本题是二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；找出数量关系，正确列出一元一次不等式．
 

22.【答案】解：如图，即为所求；
如图，即为所求；
如图，直线即为所求；
如图，点即为所求．
 

【解析】利用平移变换的性质分别作出，，的对应点，，即可；
利用轴对称变换的性质分别作出，，的对应点，，即可；
过和的中点作直线即可；
作点关于直线的对称点，连接交直线于点，点即为所求．
考查作图轴对称变换，平移变换，轴对称最短问题等知识，解题的关键是掌握轴对称变换的性质，属于中考常考题型．
 

23.【答案】 

【解析】解：，
得：，即，
：，
得，，
把代入得
所以这个方程组的解是；

得：，即，
得：，
得，，
把代入得
这个方程组的解是．
故答案为：．
先计算得，再运用题目中的方法求解此方程组的解；
先计算得，再运用题目中的方法求解此方程组的解．
本题考查了解二元一次方程组，根据方程组的特点进行准确变形是解题的关键．
 

24.【答案】   

【解析】解：将绕着的中点旋转得到，
≌，
，，
四边形是平行四边形，
，，
，
，
，
故答案为：，；
点秒运动，，
；
点秒运动，
则，
当将四边形的周长分成：两部分时，
或，
解得或，
经检验，和是原方程的根，
当将四边形的周长分成：两部分时，的值为或；
如图，

当时，，
，
点与点关于对称，
；
如图，

当时，
，
点与点关于对称，
，
综上所述，的度数为或．
将绕着的中点旋转得到，则≌，则，，从而判定四边形是平行四边形，，根据求出；
点秒运动，，表示出；
先用表示四边形的各个线段的长度，当将四边形的周长分成：两部分时，分两种情况讨论即可；
当与四边形的边垂直时，有两种情况，画出图形，求解即可．
本题是四边形综合题目，考查了平行四边形的性质，图形的旋转等知识；本题综合性强，有一定难度，根据点的运动情况表示出各个线段的长是解题的关键．