沪科版九年级上册23.1 锐角的三角函数优质教学ppt课件

这是一份沪科版九年级上册23.1 锐角的三角函数优质教学ppt课件，共20页。PPT课件主要包含了导入新课，回顾与思考，讲授新课，引出定义，典例精析，探究归纳，方法总结，在Rt△BCD中，当堂练习，在Rt△ABC中等内容，欢迎下载使用。

1.理解并掌握锐角正弦、余弦的定义，并进行相关计算； （重点、难点）2.在直角三角形中求正弦值、余弦值. (重点)
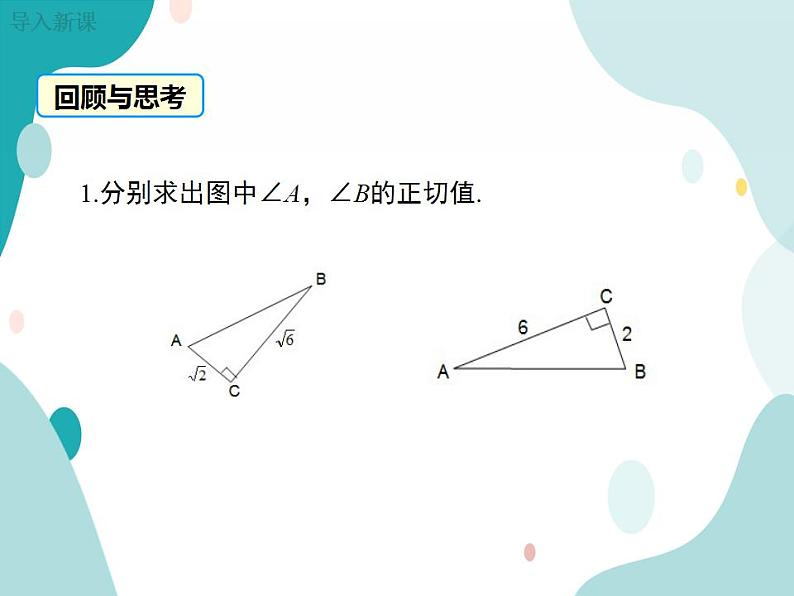
1.分别求出图中∠A，∠B的正切值.
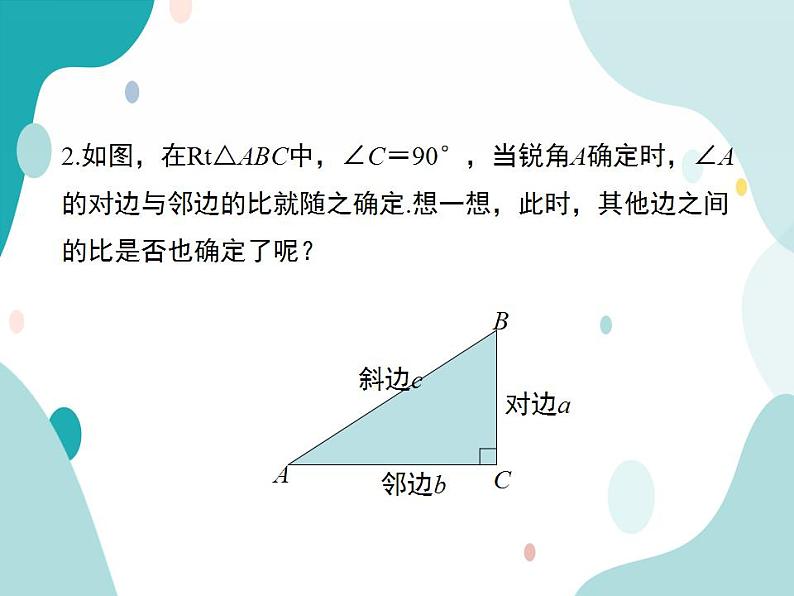
2.如图，在Rt△ABC中，∠C＝90°，当锐角A确定时，∠A的对边与邻边的比就随之确定.想一想，此时，其他边之间的比是否也确定了呢？
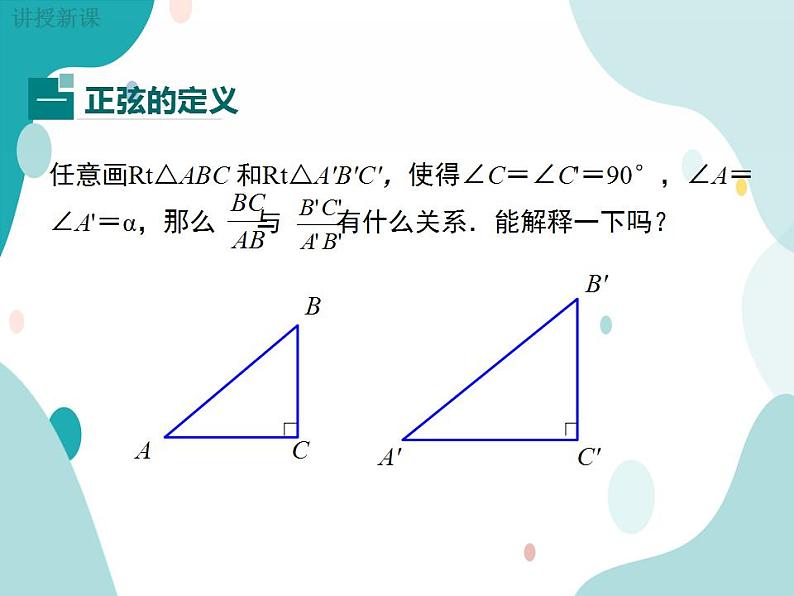
任意画Rt△ABC 和Rt△A'B'C'，使得∠C＝∠C'＝90°，∠A＝∠A'＝α，那么 与 有什么关系．能解释一下吗？
在图中，由于∠C＝∠C'＝90°，∠A＝∠A'＝α，所以Rt△ABC∽Rt△A'B'C'
这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比也是一个固定值．
如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦（sine），记作sinA 即
例如，当∠A＝30°时，我们有
当∠A＝45°时，我们有
例1 在Rt△ABC中，∠C＝90°，a＝3，c＝5，求sinA和tanA的值．
分析：先根据勾股定理求出b的长，再根据锐角三角函数的定义求解．
解：在Rt△ABC中，c＝5，a＝3，
【方法总结】解决这类问题的关键是利用勾股定理求出直角三角形的其他边的长，再利用锐角三角函数的定义求三角函数的值．
如图，在Rt△ABC中，∠C＝90°，当锐角A确定时，∠A的对边与斜边的比就随之确定，此时，其他边之间的比是否也确定了呢？为什么？
任意画Rt△ABC 和Rt△A'B'C'，使得∠C＝∠C'＝90°，∠B＝∠B'＝α，那么 与 有什么关系．能解释一下吗？
在图中，由于∠C＝∠C'＝90°，∠B＝∠B'＝α，所以Rt△ABC∽Rt△A'B'C'
这就是说，在直角三角形中，当锐角B的度数一定时，不管三角形的大小如何，∠B的邻边与斜边的比也是一个固定值．
当锐角B的大小确定时，我们把∠B的邻边与斜边的比叫做∠B的余弦（csine），记作csB，即
1.sinA、csA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)、 csA是一个比值（数值）、 csA的大小只与∠A的大小有关，而与直角三角形的边长无关.
如图：在Rt △ABC中，∠C＝90°，
解析：图中无直角三角形，需构造直角三角形，然后结合勾股定理，利用锐角三角函数的定义求解．过点P作PH⊥x轴，垂足为点H，如图．在Rt△OPH中，∵PH＝b，OH＝a，在Rt△ABC中，c＝5，a＝3，
例2 如图,已知点P在第一象限,其坐标是(a,b)，则csα等于(　　)
也可以过点P作PM⊥y轴于点M，注意点P(a，b)到x轴的距离是|b|，到y轴的距离是|a|，若点P不在第一象限，则要注意字母的符号．
1.如图，Rt△ABC中，∠ACB=90°，CD⊥AB，图中sinB可由哪两条线段比求得？
解：在Rt△ABC中，
因为∠B=∠ACD，所以
求一个角的正弦值，除了用定义直接求外，还可以转化为求和它相等角的正弦值.
2. 如图，在Rt△ABC中，∠C＝90°，AB =10，BC＝6，求sinA、csA、tanA的值．
3. 如图，在Rt△ABC中，∠C＝90°，csA＝ ，求sinA、tanA的值．
设AC=15k，则AB=17k
4. 如图，在Rt△ABC中，∠C＝90°，AC＝8，tanA＝ ，求：sinA、csB的值．