数学沪科版22.4 图形的位似变换精品教学课件ppt

这是一份数学沪科版22.4 图形的位似变换精品教学课件ppt，共15页。PPT课件主要包含了学习目标，导入新课，讲授新课，合作探究，当堂练习，－10等内容，欢迎下载使用。

1.理解位似图形的坐标变换规律.（难点）2.能熟练在坐标系中根据坐标的变化规律做出位似图形.(重点)
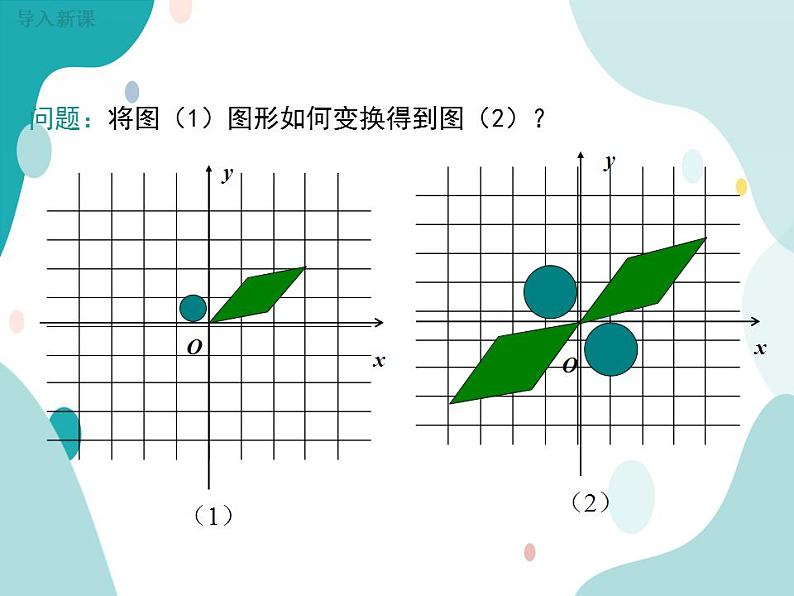
问题：将图（1）图形如何变换得到图（2）？
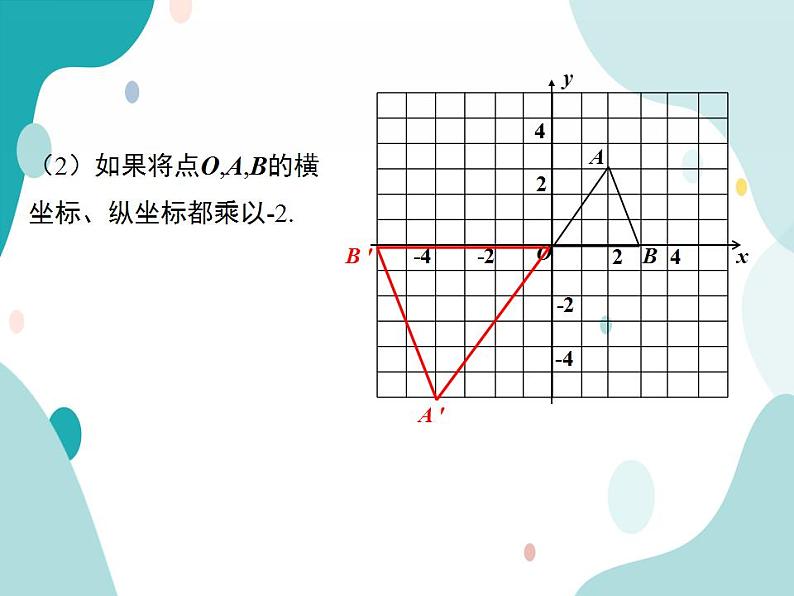
问题1：在平面直角坐标系中，△OAB三个顶点的坐标分别为O(0,0), A(3，0), B(2，3)
（1）将点O,A,B的横坐标、纵坐标都乘2，得到三个点，以这三个点位为顶点的三角形与△OAB位似吗？如果位似，指出位似中心和相似比.
位似,位似中心为原点O，相似比为1:2
（2）如果将点O,A,B的横坐标、纵坐标都乘以-2.
在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0)，所对应的图形与原图形位似，位似中心是坐标原点，它们的相似比为|k|.
例1：在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，0)，A(6，0),B(3，6),C(-3，3).以原点O为位似中心，画出四边形OABC的位似图形，使它与四边形OABC的相似比是2:3.
画法一：如右图所示，解：将四边形OABC各顶点的坐标都乘 ；在平面直角坐标系中描点O(0,0), A'(4,0),B'(2,4)C(-2,-2);在平面直角坐标系中描点A',B',C',用线段顺次连接O,A',B',C'.
画法二：如右图所示解：将四边形OABC各顶点的坐标都乘 ；在平面直角坐标系中描点O(0,0), A''(-4,0),B'' (-2,-4),C(2,-2);在平面直角坐标系中描点A'',B'', C'',用线段顺次连接O,A'',B'',C''.
一般情况下，若没有限定象限，画已知图形关于某点的相似图形有2个.
例2：在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以R(0，-1)为位似中心,相似比为2,将△ABC放大.
放大后对应点的坐标分别是多少?
在平面直角坐标系中，如果位似变换是以任意点(a,b)为位似中心，相似比为k，那么位似图形对应点的坐标(x,y)等于原来点的坐标(m,n)进行以下变换： x=a _ k(m-a) y=b _ k(n-b)
1.在平面直角坐标系中，已知点A(6，4),B(4，-2),以原点O为位似中心，相似比为 ，把△ABO缩小，则点A的对应点A'的坐标是（ ）A.(3，2) B.(12，8)或（-12，8） C.(12，8) D.(3，2)或（-3，-2）
2. 如图，四边形ABCD的坐标分别为A（－6，6），B（－8，2），C（－4，0），D（－2，4），画出它的一个以原点O为位似中心，相似比为 的位似图形．
解：如图，利用位似变换中对应点的坐标的变化规律．分别取点A'（ ， ），B ' （ ， ），C ' （ ， ），D'（ ， ）．
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形．
3.如图，△ABC三个顶点坐标分别为A（2，－2），B（4，－5），C（5，－2），以原点O为位似中心，将这个三角形放大为原来的2倍．
解：A'（ ， ），B ' （ ， ），C ' （ ， ），
A" （ ， ），B" （ ， ），C" （ ， ），