【最新版】高中数学高三培优小题练第62练　立体几何小题易错练

这是一份【最新版】高中数学高三培优小题练第62练　立体几何小题易错练，共8页。试卷主要包含了以下命题等内容，欢迎下载使用。
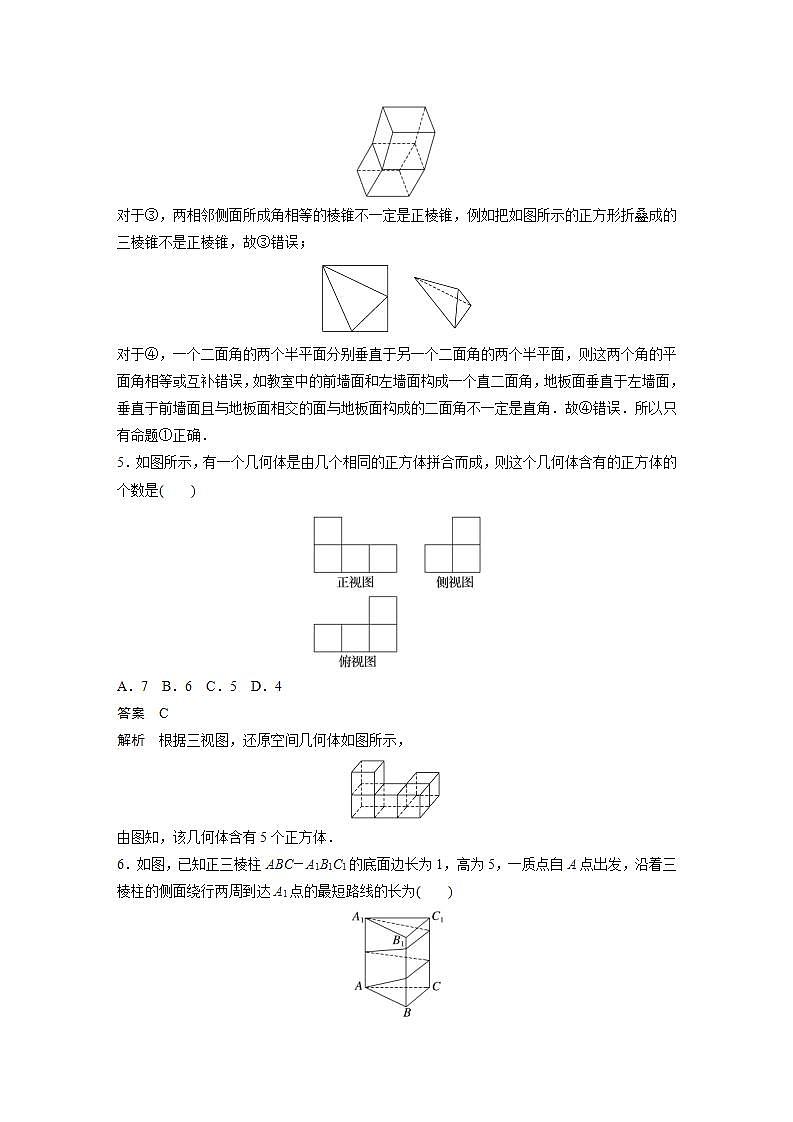
第62练　立体几何小题易错练1．已知角α的两边和角β的两边分别平行，且α＝20°，则β等于(　　)A．20°   B．160°C．20°或160°   D．不能确定答案　C解析　因为角α的两边和角β的两边分别平行，所以α，β相等或者互补，所以β＝20°或160°.2．对于空间中的两条不同直线m，n和一个平面α，下列命题正确的是(　　)A．若m∥α，n∥α，则m∥nB．若m∥α，m∥n，则n∥αC．若m∥n，n⊂α，则m∥αD．若m⊥α，n⊥α，则m∥n答案　D解析　对于选项A，若m∥α，n∥α，则m，n可能平行、相交或者异面，所以A不正确；对于选项B，若m∥α，m∥n，则n∥α或者n⊂α，所以B不正确；对于选项C，若m∥n，n⊂α，则m∥α或者m⊂α，所以C不正确；对于选项D，垂直于同一平面的两条直线平行，所以D正确．3．“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案　B解析　设命题p：直线l与平面α内无数条直线垂直，命题q：直线l与平面α垂直，则p⇒/ q，但q⇒p，所以p是q的必要不充分条件．4．以下命题：①根据斜二测画法，三角形的直观图是三角形；②有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱；③两相邻侧面所成角相等的棱锥是正棱锥；④若两个二面角的半平面互相垂直，则这两个二面角的大小相等或互补．其中正确命题的个数为(　　)A．1  B．2  C．3  D．4答案　A解析　对于①，由斜二测画法规则知，三角形的直观图是三角形，故①正确；对于②，如图符合条件但却不是棱柱，故②错误；对于③，两相邻侧面所成角相等的棱锥不一定是正棱锥，例如把如图所示的正方形折叠成的三棱锥不是正棱锥，故③错误；对于④，一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个角的平面角相等或互补错误，如教室中的前墙面和左墙面构成一个直二面角，地板面垂直于左墙面，垂直于前墙面且与地板面相交的面与地板面构成的二面角不一定是直角．故④错误．所以只有命题①正确．5．如图所示，有一个几何体是由几个相同的正方体拼合而成，则这个几何体含有的正方体的个数是(　　)A．7  B．6  C．5  D．4答案　C解析　根据三视图，还原空间几何体如图所示，由图知，该几何体含有5个正方体．6．如图，已知正三棱柱ABC－A1B1C1的底面边长为1，高为5，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为(　　)A．12   B．13C.   D．15答案　C解析　将正三棱柱ABC－A1B1C1沿侧棱展开，再拼接一次，其侧面展开图如图所示，在展开图中，最短距离是六个矩形对角线的连线的长度，即为三棱柱的侧面上所求距离的最小值．由已知求得矩形的长等于6×1＝6，宽等于5，由勾股定理得d＝＝.7．《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍．其中记载有求“囷盖”的术：“置如其周，令相承也．又以高乘之，三十六成一”．该术相当于给出了由圆锥的底面周长L与高h，计算其体积V≈L2h的近似公式．它实际上是将圆锥体积公式中的圆周率近似取为3.那么近似公式V≈L2h相当于将圆锥体积公式中的圆周率近似取为(　　)A.  B.  C.  D.答案　C解析　设圆锥底面圆的半径为r，则V＝πr2h，又V≈L2h＝(2πr)2h，故(2πr)2h≈πr2h，所以π≈＝.8．(2022·哈尔滨模拟)如图，在正方体ABCD－A1B1C1D1中，E，F，G分别为AD，B1B，D1C1上靠近A，B1，D1的三等分点，M1，M2，N1，N2，P1，P2分别是AB，B1C1，DD1的三等分点，M3，N3，P3分别是AB，B1C1，DD1的中点，则平面EFG过(　　)A．M1，N1，P1   B．M2，N2，P2C．M3，N3，P3   D．以上都不正确答案　A解析　如图所示，设正方体的棱长为3，取CD的三等分点H，则GH∥FB，所以延长GF与HB的延长线交于点P，连接PE并延长，分别交AB和CD延长线于N，Q，连接QG交D1D于点M，过点G作GZ∥EN交B1C1于点Z.平面EFG截正方体所得截面即为ENFZGM，设AN＝x，易知＝＝，所以＝＝，＝＝，所以QD＝2x，QH＝2x＋1，＝，解得x＝1，所以点N与M1重合，QD＝2，＝＝，所以点M与P1重合，因为GZ∥EN，所以点Z与N1重合．9.如图，正方体ABCD－A1B1C1D1的棱长为4，动点E，F在棱A1B1上，动点P，Q分别在棱AD，CD上．若EF＝2，A1E＝m，DQ＝n，DP＝p(m，n，p大于零)，则四面体PEFQ的体积(　　)A．与m，n，p都有关B．与m有关，与n，p无关C．与p有关，与m，n无关D．与n有关，与m，p无关答案　C解析　四面体PEFQ的体积VP－EFQ＝·S△EFQ·h(h为点P到平面EFQ的距离)．S△EFQ＝×EF×DA1＝×2×4＝4为定值，与m，n无关，点P到平面EFQ的距离即为点P到平面A1B1CD的距离，与点P的位置有关，即与p有关．10．如图，在三棱锥P－ABC中，D，E，F分别为棱PC，AC，AB的中点，PA⊥平面ABC，∠ABC＝90°，AB＝PA＝6，BC＝8，则下列说法不正确的是(　　)A．三棱锥D－BEF的体积为6B．直线PB与直线DF垂直C．平面DEF截三棱锥P－ABC所得的截面面积为12D．点P与点A到平面BDE的距离相等答案　B解析　对于A选项，∵D，E分别为PC，AC的中点，则DE∥PA，且DE＝PA＝3，∵PA⊥平面ABC，∴DE⊥平面ABC，∵F为AB的中点，∠ABC＝90°，∴S△BEF＝S△ABE＝S△ABC＝××6×8＝6，∴VD－BEF＝S△BEF·DE＝×6×3＝6，故A选项正确；对于B选项，∵PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA，又∵∠ABC＝90°，即BC⊥AB，且PA∩AB＝A，PA，AB⊂平面PAB，∴BC⊥平面PAB，∵E，F分别为AC，AB的中点，∴EF∥BC，∴EF⊥平面PAB，∵AB⊂平面PAB，∴EF⊥AB，∵DE⊥平面ABC，AB⊂平面ABC，∴AB⊥DE，∵EF∩DE＝E，DE，EF⊂平面DEF，∴AB⊥平面DEF，∵DF⊂平面DEF，∴AB⊥DF，假设DF⊥PB，∵AB∩PB＝B，AB，PB⊂平面PAB，∴DF⊥平面PAB，而过点F有且只有一条直线与平面PAB垂直，故B选项错误；对于C选项，取PB的中点M，连接DM，FM，如图，∵D，M分别为PC，PB的中点，∴DM∥BC且DM＝BC，同理可得EF∥BC且EF＝BC，∴EF∥DM且EF＝DM，四边形DEFM为平行四边形，则平面DEF截三棱锥P－ABC所得的截面为平行四边形DEFM，易知DE⊥EF，且DE＝PA＝3，EF＝BC＝4，∴S▱DEFM＝DE·EF＝12，故C选项正确；对于D选项，∵DE∥PA，PA⊄平面BDE，DE⊂平面BDE，∴PA∥平面BDE，∴点P与点A到平面BDE的距离相等，故D选项正确．11．将一个棱长为3 cm的正方体铁块磨成一个球体零件，则可能制作的最大零件的体积为________cm3.答案　解析　正方体的棱长为3 cm，所以最大球体的半径R＝ cm，所以球的体积V＝πR3＝ cm3.12．(2022·北京模拟)将底面直径为8，高为2的圆锥体石块打磨成一个圆柱，则该圆柱侧面积的最大值为________．答案　4π解析　欲使圆柱侧面积最大，需使圆柱内接于圆锥，如图所示．设圆柱的高为h，底面半径为r，则＝，解得h＝2－r，所以S圆柱侧＝2πrh＝2πr＝π，当r＝2时，S圆柱侧取得最大值4π.13．已知α，β是两个不同的平面，m，n是平面α及β之外的两条不同的直线，给出下列四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______．(用序号及⇒表示)答案　①③④⇒②(或②③④⇒①)解析　∵α，β是两个不同的平面，m，n是平面α及β之外的两条不同的直线，若①m⊥n，③n⊥β，则m∥β.又∵④m⊥α，∴②α⊥β.即①③④⇒②.若②α⊥β，③n⊥β，则n∥α.又∵④m⊥α，∴①m⊥n.即②③④⇒①.14．(2022·西北工业大学附属中学模拟)如图是四棱锥P－ABCD的平面展开图，四边形ABCD是矩形，ED⊥DC，FD⊥DA，DA＝3，DC＝2，∠FAD＝30°.在四棱锥P－ABCD中，cos∠PBC＝________.答案　解析　把平面展开图还原得到原四棱锥P－ABCD，如图，由已知ED⊥DC，FD⊥DA，可知PD⊥DC，PD⊥DA，DC∩DA＝D，∴PD⊥平面ABCD.在Rt△ADP中，∠PAD＝30°，DA＝3，故PD＝3×tan 30°＝，在Rt△CDP中， PC＝＝＝，连接DB，在矩形ABCD中，DA＝3，DC＝2，DB＝＝，在Rt△PDB中， PB＝＝＝4，在△PBC中， 利用余弦定理知cos∠PBC＝＝＝.