






人教版九年级数学上册课件:第二十一章 一元二次方程复习
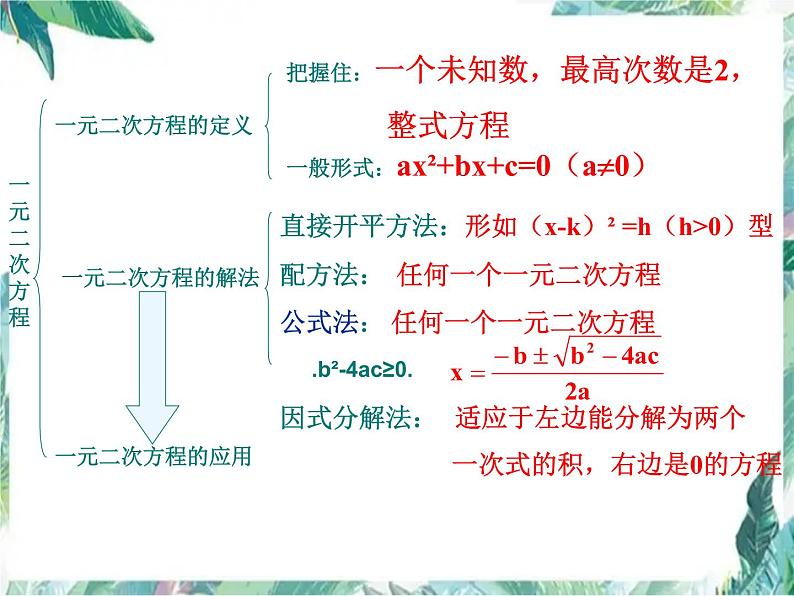
展开把握住:一个未知数,最高次数是2, 整式方程
一般形式:ax²+bx+c=0(a0)
直接开平方法:形如(x-k)² =h(h>0)型 配方法: 任何一个一元二次方程公式法: 任何一个一元二次方程因式分解法: 适应于左边能分解为两个 一次式的积,右边是0的方程
一、一元二次方程的概念
引例:判断下列方程是不是一元二次方程(1)4x- x² + =0 (2)3x² - y -1=0 (3)ax² +bx+c=0 (4)x + =0
注意:一元二次方程的 三个要素
1一个未知数,2最高次数是2, 3整式方程
巩固提高:1、若(m+2)x 2 +(m-2) x -2=0是关于x的一元二次方程则m 。2、已知关于x的方程(m²-1)x²+(m-1)x-2m+1=0,当m______ 时是一元二次方程,当m= 时是一元一次方程,当m= 时,x=0。
二、一元二次方程的解法
你还记得吗?请你选择最恰当的方法解下列一元二次方程1、3x² -1=0 2、x(2x +3)=5(2x +3)3、x² - 3 x +2=0 4、2 x ² -5x+1=0
点评:1、形如(x-k)²=h的方程可以用直接开平方法求解 2、千万记住:方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式,因为这样能把方程的一个跟丢失了,要利用因式分解法求解。 3、当方程的左边是二次三项式的时候优先用十字相乘法求解. 当我们不能利用上边的方法求解的时候就就可以用公式法求解,公式法是万能的。
练习:用最好的方法求解下列方程1、(3x -2)²-49=0 2、(3x -4)²=(4x -3)² 3、4y = 1 - y²
解:法一3x-4=±(4x-3)3x -4=4x-3或3x-4=-4x+3-x=1或 7x=7 x1 = -1, x2 =1法二(3x-4)² -(4x-3)² =0(3x-4+4x-3)(3x-4x+3)=0(7x-7)(-x-1)=0 7x-7=0或-x-1=0 x1 = -1, x2 =1
1、用配方法解方程2x² +4x +1 =0,配方后得到的方程是 。2、一元二次方程ax² +bx +c =0,若x=1是它的一个根,则a+b+c= ,若a -b+c=0,则方程必有一根为 。3、
4、方程2 x ²-mx-m² =0有一个根为 - 1, 则m= ,另一个根为 。
一元二次方程根的判别式
所以,原方程有两个不相等的实根。
说明:解这类题目时,一般要先把方程化为一般形式,求出△,然后对△进行计算,使△的符号明朗化,进而说明△的符号情况,得出结论。
1、不解方程,判别方程的根的情况
(3).当△ <0 ,方程有没有实数根, 8k+9 <0 , 即
2、根据方程的根的情况确定方程的待定系数的取值范围
说明:解此类题目时,也是先把方程化为一般形式,再算出△,再由题目给出的根的情况确定△的情况。从而求出待定系数的取值范围
解:∵方程有两个实数根∴
说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
注:能用韦达定理的前提条件为△≥0
2、用配方法证明:关于x的方程(m² -12m +37)x ² +3mx+1=0, 无论m取何值,此方程都是一元二次方程
例3:某印刷厂一月份印刷了科技书50万册,第一季度共印182万册,问二、三月份平均每月的增长率是多少?
解:设平均每月增长率是x
50+50(1+x)+50(1+x)²=182
1+1+x+ (1+x)²=3.64
2+X+1+2x+x²=3.64
X1=0.2 x2=-3.2(舍)
答:平均每月增长的百分率是20%
某工厂计划用两年时间使产值翻一翻, 并且使第二年增长的百分数是第一年增长百分数的2倍,求第二年提高的百分数.(精确到1%)
解:设第二年提高的百分数为x,
1(1+0.5x)(1+x)=2
则第一年提高的百分数为0.5x
某市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?
.若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?
.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,实验发现每多种一棵桃树,每棵树的产量就会减少2个,但多种的桃树不能超过100棵,如果要使产量增加15.2%,那么应多种多少棵桃树?
在有关增长率的问题中,要掌握等量关系:其中a为变化前的数,p为变化后的数.
用一元二次方程解数字问题
例1 两个连续奇数的积是323,求这两个数。
例2:有一个两位数等于其数字之积的3倍,其十位数字比个位数字小2,求这两位数。
3 有一个两位数,它们的十位数字与个位数字之和为8,如果把十位数字与个位数字调换后,所得的两位数乘以原来的两位数就得1855,求原来的两位数。
[10(8-x)+x][10x+(8-x)]=1855
解:设原来两位数的个位是x,则十位是(8-x)
x1=5 ,x2=3
答:这个数是35或53
4 一个三位数、十位数字比百位数字大3,个位数字等于百位数字与十位数字的和.已知这个三位数比个位数字的平方的5倍大12,求这个三位数.
解方程: 5x²-9x-18=0(公式法) 5x²+4x-1=0(配方法)3 2y(y-1)=(3-3y)(分解因式法)4 2(x+3)2=8 (直接开方法)
初中数学人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程复习课件ppt: 这是一份初中数学人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程复习课件ppt,共40页。PPT课件主要包含了基础回顾,未知数最高次数是1,未知数最高次数是2,不相等,x1=x2=0,完全平方,一次项系数一半的平方,判别式概念,判别式表示,传染源等内容,欢迎下载使用。
初中数学人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程复习课件ppt: 这是一份初中数学人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程复习课件ppt,共16页。PPT课件主要包含了导入课题,复习目标,b2-4ac,b2-4ac0,二次项系数,一次项系数,常数项,一元二次方程,一个未知数,最高次是2等内容,欢迎下载使用。
2021学年数学活动多媒体教学ppt课件: 这是一份2021学年数学活动多媒体教学ppt课件,共25页。PPT课件主要包含了导入课题,活动目标,活动1,三角形点阵,活动2,正六边形点阵,①填写下表,n-1,n+3,n+2等内容,欢迎下载使用。












