初中数学浙教版九年级上册2.4 概率的简单应用教学ppt课件

这是一份初中数学浙教版九年级上册2.4 概率的简单应用教学ppt课件，共19页。PPT课件主要包含了新知导入，复习回顾，合作学习，提炼概念，概率的简单应用，概率的计算公式，估计概率，典例精讲，新知讲解，练一练等内容，欢迎下载使用。

1.如果有人买了彩票，一定希望知道中奖的概率有多大．那么怎么样来估计中奖的概率呢？
2.出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小？
概率与人们生活密切相关，在生活，生产和科研等各个领域都有着广泛的应用．
由上面两个问题，你能得到什么？
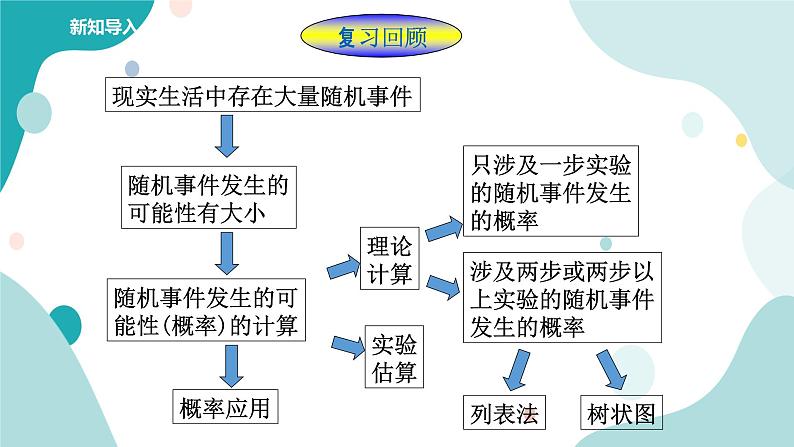
在实际生活中，我们常用频率来估计概率，在大量重复的实验中发现频率接近于哪个数，把这个数作为概率．
例1 某商场举办有奖销售活动，每张奖券获奖的可能性相同，以每10000张奖券为一个开奖单位，设特等奖１个，一等奖10个，二等奖100个，问１张奖券中一等奖的概率是多少？中奖的概率是多少？
解:因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),所以1张奖券中奖的概率是
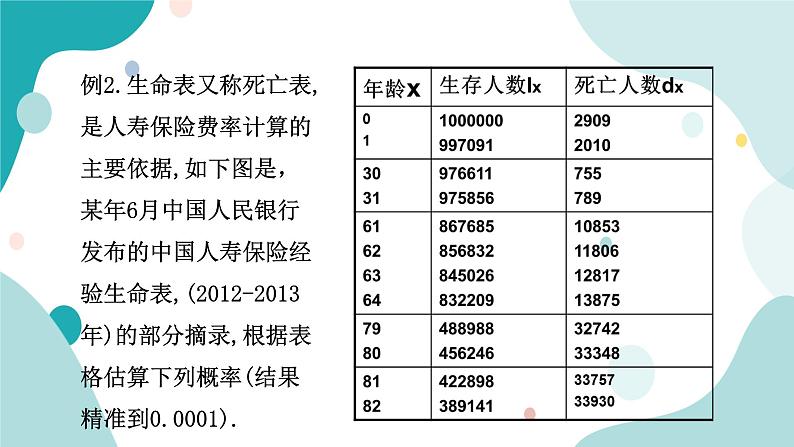
例2.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是，某年6月中国人民银行发布的中国人寿保险经验生命表,(2012-2013年)的部分摘录,根据表格估算下列概率(结果精准到0.0001).
(1)某人今年61岁,他当年死亡的概率.(2)某人今年31岁,他活到62岁的概率.
答:他当年死亡的概率约为0.01251,活到62岁的概率约为0.8780.
根据生命表回答下列问题：(1)一个80岁的人在当年死亡的概率是多少?(2)一个61岁的人,他活到82岁的概率是多少?(3)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?
(3)因为一万人在80岁当年死去的人数为：10000×0.0731=731人，所以保险公司应支付赔偿金为731a元
1.如图所示，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：顾客每购买100元的商品，就可获得一次转动转盘的机会，如果转盘停止后，指针这个好对准红、黄和绿色区域，顾客就可以分别获得100元、50元、20元的购物券.
（1）甲顾客购物80元，他获得转动转盘的机会的概率是多少？ （2）以顾客购物180元，他获得转动转盘的机会的概率是多少？他得到100元、50元、20元的购物券的机会的概率分别是多少？
解：(1)因为80<100，所以甲获得转动转盘的机会的概率是0；
(2)因为100<180<200，所以乙获得转动转盘的机会的概率是1，即得到一次转动转盘的机会．
2.　保险公司为了确定人寿保险的价格，需要对一定范围内人的寿命进行调查统计，制定一张生命表，现把某地区的生命表的部分摘录如下：
根据上表解下列问题：(1)某人今年40岁，他当年去世的概率是多少？他活到80岁的概率是多少？(2)如果有10 000个40岁的人参加人寿保险，当年死亡的人均赔偿金为a元，预计保险公司需付的赔偿总额为多少元？
3.在课外活动时间，小王、小丽、小华做“互相踢毽子”游戏，毽子从一人传到另一人就记为踢一次．(1)用树状图或列表法说明，从小丽开始，经过两次踢毽后，毽子踢到小华处的概率是多少；(2)若经过三次踢毽后，毽子踢到小王处的可能性最小，应确定从谁开始踢，并说明理由．
解：(1)树状图如图所示：