2022年辽宁大连甘井子区育文中学初中数学毕业考试模拟冲刺卷含解析

这是一份2022年辽宁大连甘井子区育文中学初中数学毕业考试模拟冲刺卷含解析，共18页。试卷主要包含了下列运算正确的是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．国家主席习近平在2018年新年贺词中说道：“安得广厦千万间，大庇天下寒士俱欢颜！2017年我国3400000贫困人口实现易地扶贫搬迁、有了温暖的新家．”其中3400000用科学记数法表示为（　　）
A．0.34×107 B．3.4×106 C．3.4×105 D．34×105
2．如图，在▱ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF=4，则下列结论：①；②S△BCE=36；③S△ABE=12；④△AEF～△ACD，其中一定正确的是（　　）

A．①②③④ B．①④ C．②③④ D．①②③
3．如图，直线y=3x+6与x，y轴分别交于点A，B，以OB为底边在y轴右侧作等腰△OBC，将点C向左平移5个单位，使其对应点C′恰好落在直线AB上，则点C的坐标为（　　）

A．（3，3） B．（4，3） C．（﹣1，3） D．（3，4）
4．把不等式组的解集表示在数轴上，下列选项正确的是（　　）
A． B．
C． D．
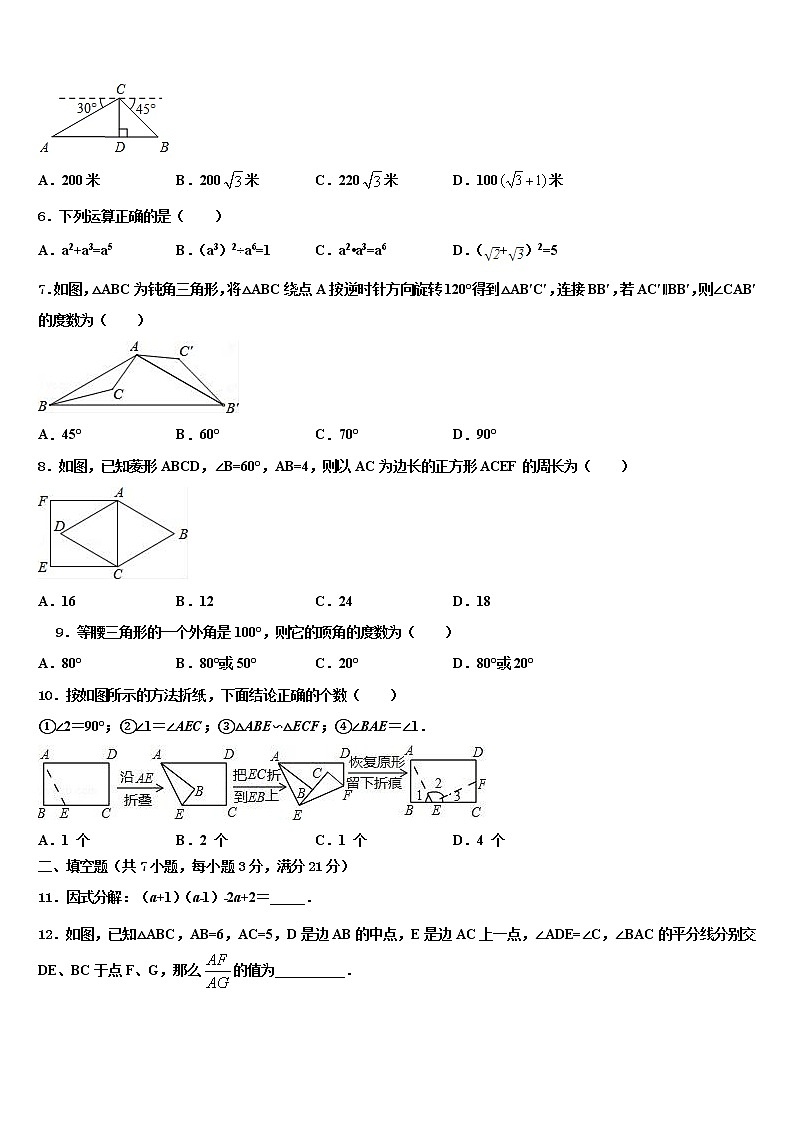
5．如图，在热气球C处测得地面A、B两点的俯角分别为30°、45°，热气球C的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是（　　）

A．200米 B．200米 C．220米 D．100米
6．下列运算正确的是（　　）
A．a2+a3=a5 B．（a3）2÷a6=1 C．a2•a3=a6 D．（+）2=5
7．如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（　　）

A．45° B．60° C．70° D．90°
8．如图，已知菱形ABCD，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为（　　）

A．16 B．12 C．24 D．18
9．等腰三角形的一个外角是100°，则它的顶角的度数为（　　）
A．80° B．80°或50° C．20° D．80°或20°
10．按如图所示的方法折纸，下面结论正确的个数（ ）
①∠2＝90°；②∠1＝∠AEC；③△ABE∽△ECF；④∠BAE＝∠1．

A．1 个 B．2 个 C．1 个 D．4 个
二、填空题（共7小题，每小题3分，满分21分）
11．因式分解：（a+1）（a﹣1）﹣2a+2＝_____．
12．如图，已知△ABC，AB=6，AC=5，D是边AB的中点，E是边AC上一点，∠ADE=∠C，∠BAC的平分线分别交DE、BC于点F、G，那么的值为__________．

13．如图，在矩形ABCD中，AD=5，AB=4，E是BC上的一点，BE=3，DF⊥AE，垂足为F，则tan∠FDC=_____．

14．已知a，b为两个连续的整数，且a＜＜b，则ba＝_____．
15．如图，边长一定的正方形ABCD，Q是CD上一动点，AQ交BD于点M，过M作MN⊥AQ交BC于N点，作NP⊥BD于点P，连接NQ，下列结论：①AM=MN；
②MP=BD；③BN+DQ=NQ；④为定值。其中一定成立的是_______.

16．关于x的一元二次方程x2+2x+k=0有两个不相等的实数根，则k的取值范围是_____．
17．当x=_________时，分式的值为零．
三、解答题（共7小题，满分69分）
18．（10分）某初中学校组织200位同学参加义务植树活动．甲、乙两位同学分别调查了30位同学的植树情况，并将收集的数据进行了整理，绘制成统计表1和表2：
表1：甲调查九年级30位同学植树情况
每人植树棵数
7
8
9
10
人数
3
6
15
6
表2：乙调查三个年级各10位同学植树情况
每人植树棵数
6
7
8
9
10
人数
3
6
3
12
6
根据以上材料回答下列问题：
（1）关于于植树棵数，表1中的中位数是　 　棵；表2中的众数是　 　棵；
（2）你认为同学　 　（填“甲”或“乙”）所抽取的样本能更好反映此次植树活动情况；
（3）在问题（2）的基础上估计本次活动200位同学一共植树多少棵？
19．（5分） “足球运球”是中考体育必考项目之一．兰州市某学校为了解今年九年级学生足球运球的掌握情况，随机抽取部分九年级学生足球运球的测试成绩作为一个样本，按A，B，C，D四个等级进行统计，制成了如下不完整的统计图．（说明：A级：8分﹣10分，B级：7分﹣7.9分，C级：6分﹣6.9分，D级：1分﹣5.9分）
根据所给信息，解答以下问题：
（1）在扇形统计图中，C对应的扇形的圆心角是_____度；
（2）补全条形统计图；
（3）所抽取学生的足球运球测试成绩的中位数会落在_____等级；
（4）该校九年级有300名学生，请估计足球运球测试成绩达到A级的学生有多少人？

20．（8分）某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球20个，B种品牌的足球30个，共花费4600元，已知购买4个B种品牌的足球与购买5个A种品牌的足球费用相同．
（1）求购买一个A种品牌、一个B种品牌的足球各需多少元．
（2）学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共42个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高5元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的80%，且保证这次购买的B种品牌足球不少于20个，则这次学校有哪几种购买方案？
（3）请你求出学校在第二次购买活动中最多需要多少资金？
21．（10分）某商场用24000元购入一批空调，然后以每台3000元的价格销售，因天气炎热，空调很快售完，商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，每台的售价也上调了200元．商场第一次购入的空调每台进价是多少元？商场既要尽快售完第二次购入的空调，又要在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售，最多可将多少台空调打折出售？
22．（10分）如图，B、E、C、F在同一直线上，AB＝DE，BE＝CF，∠B＝∠DEF，求证：AC＝DF．

23．（12分）如图，AB是⊙O的直径，点C是AB延长线上的点，CD与⊙O相切于点D，连结BD、AD．求证；∠BDC＝∠A．若∠C＝45°，⊙O的半径为1，直接写出AC的长．

24．（14分）如图，已知A（a，4），B（﹣4，b）是一次函数与反比例函数图象的两个交点．

（1）若a＝1，求反比例函数的解析式及b的值；
（2）在（1）的条件下，根据图象直接回答：当x取何值时，反比例函数大于一次函数的值？
（3）若a﹣b＝4，求一次函数的函数解析式．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、B
【解析】
解：3400000=.
故选B.
2、D
【解析】
∵在▱ABCD中，AO=AC，
∵点E是OA的中点，
∴AE=CE，
∵AD∥BC，
∴△AFE∽△CBE，
∴=，
∵AD=BC，
∴AF=AD，
∴；故①正确；
∵S△AEF=4， =（）2=，
∴S△BCE=36；故②正确；
∵ =，
∴=，
∴S△ABE=12，故③正确；
∵BF不平行于CD，
∴△AEF与△ADC只有一个角相等，
∴△AEF与△ACD不一定相似，故④错误，故选D．
3、B
【解析】
令x=0，y=6，∴B（0，6），
∵等腰△OBC，∴点C在线段OB的垂直平分线上，
∴设C（a，3），则C '（a－5，3），
∴3=3（a－5）+6，解得a=4，
∴C（4，3）.
故选B.
点睛：掌握等腰三角形的性质、函数图像的平移.
4、C
【解析】
求得不等式组的解集为x＜﹣1，所以C是正确的．
【详解】
解：不等式组的解集为x＜﹣1．
故选C．
【点睛】
本题考查了不等式问题，在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
5、D
【解析】
在热气球C处测得地面B点的俯角分别为45°，BD=CD=100米，再在Rt△ACD中求出AD的长，据此即可求出AB的长．
【详解】
∵在热气球C处测得地面B点的俯角分别为45°，
∴BD＝CD＝100米，
∵在热气球C处测得地面A点的俯角分别为30°，
∴AC＝2×100＝200米，
∴AD＝＝100米，
∴AB＝AD+BD＝100+100＝100（1+）米，
故选D．
【点睛】
本题考查了解直角三角形的应用--仰角、俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形．
6、B
【解析】
利用合并同类项对A进行判断；根据幂的乘方和同底数幂的除法对B进行判断；根据同底数幂的乘法法则对C进行判断；利用完全平方公式对D进行判断．
【详解】
解：A、a2与a3不能合并，所以A选项错误；
B、原式=a6÷a6=1，所以A选项正确；
C、原式=a5，所以C选项错误；
D、原式=2+2+3=5+2，所以D选项错误．
故选：B．
【点睛】
本题考查同底数幂的乘除、二次根式的混合运算，：二次根式的混合运算先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．解题关键是在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
7、D
【解析】
已知△ABC绕点A按逆时针方向旋转l20°得到△AB′C′，根据旋转的性质可得∠BAB′=∠CAC′=120°，AB=AB′，根据等腰三角形的性质和三角形的内角和定理可得∠AB′B=（180°-120°）=30°，再由AC′∥BB′，可得∠C′AB′=∠AB′B=30°，所以∠CAB′=∠CAC′-∠C′AB′=120°-30°=90°．故选D．
8、A
【解析】
由菱形ABCD，∠B=60°，易证得△ABC是等边三角形，继而可得AC=AB=4，则可求得以AC为边长的正方形ACEF的周长．
【详解】
解：∵四边形ABCD是菱形，∴AB=BC．
∵∠B=60°，∴△ABC是等边三角形，∴AC=AB=BC=4，∴以AC为边长的正方形ACEF的周长为：4AC=1．
故选A．
【点睛】
本题考查了菱形的性质、正方形的性质以及等边三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
9、D
【解析】
根据邻补角的定义求出与外角相邻的内角，再根据等腰三角形的性质分情况解答．
【详解】
∵等腰三角形的一个外角是100°，
∴与这个外角相邻的内角为180°−100°=80°，
当80°为底角时，顶角为180°-160°=20°，
∴该等腰三角形的顶角是80°或20°.
故答案选：D.
【点睛】
本题考查了等腰三角形的性质，解题的关键是熟练的掌握等腰三角形的性质.
10、C
【解析】
∵∠1+∠1=∠2，∠1+∠1+∠2=180°，
∴∠1+∠1=∠2=90°，故①正确；
∵∠1+∠1=∠2，∴∠1≠∠AEC.故②不正确；
∵∠1+∠1=90°，∠1+∠BAE=90°,
∴∠1=∠BAE,
又∵∠B＝∠C,
∴△ABE∽△ECF.故③，④正确；
故选C.

二、填空题（共7小题，每小题3分，满分21分）
11、（a﹣1）1．
【解析】
提取公因式（a−1），进而分解因式得出答案．
【详解】
解：（a+1）（a﹣1）﹣1a+1
＝（a+1）（a﹣1）﹣1（a﹣1）
＝（a﹣1）（a+1﹣1）
＝（a﹣1）1．
故答案为：（a﹣1）1．
【点睛】
此题主要考查了提取公因式法分解因式，找出公因式是解题关键．
12、
【解析】
由题中所给条件证明△ADF△ACG，可求出的值.
【详解】
解：在△ADF和△ACG中，
AB=6，AC=5，D是边AB的中点
AG是∠BAC的平分线，
∴∠DAF=∠CAG
∠ADE＝∠C
∴△ADF△ACG
∴.
故答案为.
【点睛】
本题考查了相似三角形的判定和性质，难度适中，需熟练掌握.
13、
【解析】
首先根据矩形的性质以及垂线的性质得到∠FDC＝∠ABE，进而得出tan∠FDC＝tan∠AEB＝，即可得出答案.
【详解】
∵DF⊥AE，垂足为F，∴∠AFD＝90°，∵∠ADF＋∠DAF＝90°，∠ADF＋∠CDF＝90°，∴∠DAF＝∠CDF，∵∠DAF＝∠AEB，∴∠FDC＝∠ABE，∴tan∠FDC＝tan∠AEB＝，∵在矩形ABCD中，AB＝4，E是BC上的一点，BE＝3，∴tan∠FDC＝.故答案为.
【点睛】
本题主要考查了锐角三角函数的关系以及矩形的性质，根据已知得出tan∠FDC＝tan∠AEB是解题关键.
14、1
【解析】
根据已知a＜＜b,结合a、b是两个连续的整数可得a、b的值,即可求解.
【详解】
解：∵a，b为两个连续的整数，且a＜＜b，
∴a＝2，b＝3，
∴ba＝32＝1．
故答案为1．
【点睛】
此题考查的是如何根据无理数的范围确定两个有理数的值,题中根据的取值范围,可以很容易得到其相邻两个整数,再结合已知条件即可确定a、b的值,
15、①②③④
【解析】

①如图1，作AU⊥NQ于U，交BD于H，连接AN，AC，
∵∠AMN=∠ABC=90°，
∴A，B，N，M四点共圆，
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°，
∴∠ANM=∠NAM=45°，
∴AM=MN；
②由同角的余角相等知，∠HAM=∠PMN，
∴Rt△AHM≌Rt△MPN，
∴MP=AH=AC=BD；
③∵∠BAN+∠QAD=∠NAQ=45°，
∴在∠NAM作AU=AB=AD，且使∠BAN=∠NAU，∠DAQ=∠QAU，
∴△ABN≌△UAN,△DAQ≌△UAQ，有∠UAN=∠UAQ，BN=NU，DQ=UQ，
∴点U在NQ上，有BN+DQ=QU+UN=NQ；
④如图2，作MS⊥AB，垂足为S，作MW⊥BC，垂足为W，点M是对角线BD上的点，
∴四边形SMWB是正方形，有MS=MW=BS=BW，
∴△AMS≌△NMW
∴AS=NW，
∴AB+BN=SB+BW=2BW，
∵BW:BM=1: ，
∴.
故答案为：①②③④
点睛：本题考查了正方形的性质，四点共圆的判定，圆周角定理，等腰直角三角形的性质，全等三角形的判定和性质；熟练掌握正方形的性质，正确作出辅助线并运用有关知识理清图形中西安段间的关系，证明三角形全等是解决问题的关键.
16、k＜1
【解析】
根据一元二次方程根的判别式结合题意进行分析解答即可.
【详解】
∵关于x的一元二次方程x2+2x+k=0有两个不相等的实数根，
∴△=，
解得：.
故答案为：.
【点睛】
熟知“在一元二次方程中，若方程有两个不相等的实数根，则△=”是解答本题的关键.
17、2
【解析】
根据若分式的值为零，需同时具备两个条件：（1）分子为1；（2）分母不为1计算
即可．
【详解】
解：依题意得：2﹣x=1且2x+2≠1．
解得x=2，
故答案为2．
【点睛】
本题考查的是分式为1的条件和一元二次方程的解法，掌握若分式的值为零，需同时具备两个条件：（1）分子为1；（2）分母不为1是解题的关键．

三、解答题（共7小题，满分69分）
18、（1）9，9；（2）乙；（3）1680棵；
【解析】
（1）根据中位数定义：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数可得答案；（2）根据样本要具有代表性可得乙同学抽取的样本比较有代表性；（3）利用样本估计总体的方法计算即可．
【详解】
（1）表1中30位同学植树情况的中位数是9棵，表2中的众数是9棵；
故答案为：9，9；
（2）乙同学所抽取的样本能更好反映此次植树活动情况；
故答案为：乙；
（3）由题意可得：（3×6+6×7+3×8+12×9+6×10）÷30×200=1680（棵），
答：本次活动200位同学一共植树1680棵．
【点睛】
本题考查了抽样调查，以及中位数，解题的关键是掌握中位数定义及抽样调查抽取的样本要具有代表性．
19、（1）117；（2）答案见图；（3）B；（4）30.
【解析】
（1）先根据B等级人数及其百分比求得总人数，总人数减去其他等级人数求得C等级人数，继而用360°乘以C等级人数所占比例即可得；（2）根据以上所求结果即可补全图形；（3）根据中位数的定义求解可得；（4）总人数乘以样本中A等级人数所占比例可得．
【详解】
（1）∵总人数为18÷45%=40人，
∴C等级人数为40﹣（4+18+5）=13人，
则C对应的扇形的圆心角是360°×=117°，
故答案为：117；
（2）补全条形图如下：

（3）因为共有40个数据，其中位数是第20、21个数据的平均数，而第20、21个数据均落在B等级，
所以所抽取学生的足球运球测试成绩的中位数会落在B等级，
故答案为：B．
（4）估计足球运球测试成绩达到A级的学生有300×=30人．
【点睛】
本题考查了条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．
20、（1）购买一个A种品牌的足球需要50元，购买一个B种品牌的足球需要80元；（2）有三种方案，具体见解析；（3）3150元．
【解析】
试题分析：(1)、设A种品牌足球的单价为x元，B种品牌足球的单价为y元，根据题意列出二元一次方程组，从而求出x和y的值得出答案；(2)、设第二次购买A种足球m个，则购买B种足球(50－m)个，根据题意列出不等式组求出m的取值范围，从而得出答案；(3)、分别求出第二次购买时足球的单件，然后得出答案.
试题解析：(1) 设A种品牌足球的单价为x元，B种品牌足球的单价为y元
，解得
(2) 设第二次购买A种足球m个，则购买B种足球(50－m)个
，解得25≤m≤27
∵m为整数 ∴m＝25、26、27
(3) ∵第二次购买足球时，A种足球单价为50＋4＝54（元），B种足球单价为80×0.9＝72
∴当购买B种足球越多时，费用越高 此时25×54＋25×72＝3150（元）
21、（1）2400元；（2）8台．
【解析】
试题分析：（1）设商场第一次购入的空调每台进价是x元，根据题目条件“商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，每台的售价也上调了200元”列出分式方程解答即可；
（2）设最多将台空调打折出售，根据题目条件“在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可．
试题解析：（1）设第一次购入的空调每台进价是x元，依题意，得
解得
经检验，是原方程的解．
答：第一次购入的空调每台进价是2 400元．
（2）由（1）知第一次购入空调的台数为24 000÷2 400＝10（台），第二次购入空调的台数为10×2＝20（台）．
设第二次将y台空调打折出售，由题意，得
解得
答：最多可将8台空调打折出售．
22、见解析
【解析】
由BE＝CF可得BC＝EF，即可判定，再利用全等三角形的性质证明即可．
【详解】
∵BE＝CF，
∴，
即BC＝EF，
又∵AB＝DE，∠B＝∠DEF，
∴在与中，
，
∴，
∴AC＝DF．
【点睛】
本题主要考查了三角形全等的判定，熟练掌握三角形全等的判定定理是解决本题的关键.
23、（1）详见解析；（2）1+
【解析】
（1）连接OD，结合切线的性质和直径所对的圆周角性质，利用等量代换求解（2）根据勾股定理先求OC，再求AC.
【详解】
（1）证明：连结．如图，
与相切于点D，


是的直径，
即




（2）解：在中，
.

【点睛】
此题重点考查学生对圆的认识，熟练掌握圆的性质是解题的关键.
24、 (1) 反比例函数的解析式为y＝，b的值为﹣1；(1) 当x＜﹣4或0＜x＜1时，反比例函数大于一次函数的值；(3) 一次函数的解析式为y＝x+1
【解析】
（1）由题意得到A（1，4），设反比例函数的解析式为y＝（k≠0），根据待定系数法即可得到反比例函数解析式为y＝；再由点B（﹣4，b）在反比例函数的图象上，得到b＝﹣1；
（1）由（1）知A（1，4），B（﹣4，﹣1），结合图象即可得到答案；
（3）设一次函数的解析式为y＝mx+n（m≠0），反比例函数的解析式为y＝，因为A（a，4），B（﹣4，b）是一次函数与反比例函数图象的两个交点，得到， 解得p＝8，a＝1，b＝﹣1，则A（1，4），B（﹣4，﹣1），由点A、点B在一次函数y＝mx+n图象上，得到，解得，即可得到答案.
【详解】
（1）若a＝1，则A（1，4），
设反比例函数的解析式为y＝（k≠0），
∵点A在反比例函数的图象上，
∴4＝，
解得k＝4，
∴反比例函数解析式为y＝；
∵点B（﹣4，b）在反比例函数的图象上，
∴b＝＝﹣1，
即反比例函数的解析式为y＝，b的值为﹣1；
（1）由（1）知A（1，4），B（﹣4，﹣1），
根据图象：当x＜﹣4或0＜x＜1时，反比例函数大于一次函数的值；
（3）设一次函数的解析式为y＝mx+n（m≠0），反比例函数的解析式为y＝，
∵A（a，4），B（﹣4，b）是一次函数与反比例函数图象的两个交点，
∴，即，
①+②得4a﹣4b＝1p，
∵a﹣b＝4，
∴16＝1p，
解得p＝8，
把p＝8代入①得4a＝8，代入②得﹣4b＝8，
解得a＝1，b＝﹣1，
∴A（1，4），B（﹣4，﹣1），
∵点A、点B在一次函数y＝mx+n图象上，
∴
解得
∴一次函数的解析式为y＝x+1．
【点睛】
本题考查一次函数与反比例函数，解题的关键是待定系数法求函数解析式.