2022届浙江省宁波兴宁中学中考联考数学试题含解析

这是一份2022届浙江省宁波兴宁中学中考联考数学试题含解析，共25页。试卷主要包含了如图，将函数y＝等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（　　）

A．∠ADC B．∠ABD C．∠BAC D．∠BAD
2．已知反比例函数y=的图象在一、三象限，那么直线y=kx﹣k不经过第（　　）象限．
A．一 B．二 C．三 D．四
3．如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，其顶点坐标为A（﹣1，﹣3），与x轴的一个交点为B（﹣3，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①abc＞0；②不等式ax2+（b﹣m）x+c﹣n＜0的解集为﹣3＜x＜﹣1；③抛物线与x轴的另一个交点是（3，0）；④方程ax2+bx+c+3=0有两个相等的实数根；其中正确的是（　　）

A．①③ B．②③ C．③④ D．②④
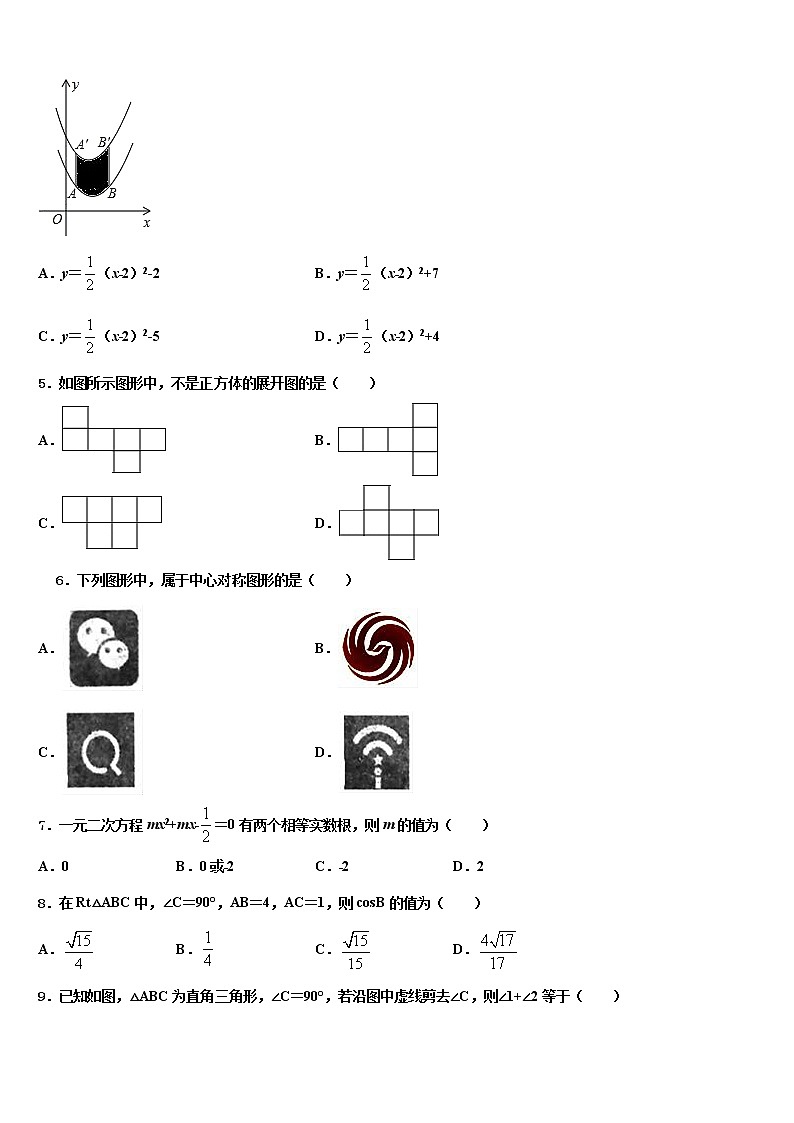
4．如图，将函数y＝（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（　　）

A．y＝（x﹣2）2-2 B．y＝（x﹣2）2+7
C．y＝（x﹣2）2-5 D．y＝（x﹣2）2+4
5．如图所示图形中，不是正方体的展开图的是（　　）
A． B．
C． D．
6．下列图形中，属于中心对称图形的是（　　）
A． B．
C． D．
7．一元二次方程mx2+mx﹣＝0有两个相等实数根，则m的值为（　　）
A．0 B．0或﹣2 C．﹣2 D．2
8．在Rt△ABC中，∠C＝90°，AB＝4，AC＝1，则cosB的值为（　　）
A． B． C． D．
9．已知如图，△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（　　）

A．315° B．270° C．180° D．135°
10．已知反比例函数y＝﹣，当﹣3＜x＜﹣2时，y的取值范围是（　　）
A．0＜y＜1 B．1＜y＜2 C．2＜y＜3 D．﹣3＜y＜﹣2
11．下列四个命题，正确的有（　　）个．
①有理数与无理数之和是有理数
②有理数与无理数之和是无理数
③无理数与无理数之和是无理数
④无理数与无理数之积是无理数．
A．1 B．2 C．3 D．4
12．如图，函数y=﹣2x+2的图象分别与x轴，y轴交于A，B两点，点C在第一象限，AC⊥AB，且AC=AB，则点C的坐标为（　　）

A．（2，1） B．（1，2） C．（1，3） D．（3，1）
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．已知一个斜坡的坡度，那么该斜坡的坡角的度数是______．
14．不等式组的解集是 _____________.
15．写出一个比大且比小的有理数：______．
16．如图，点 A 是反比例函数 y＝﹣（x＜0）图象上的点，分别过点 A 向横轴、纵轴作垂线段，与坐标轴恰好围成一个正方形，再以正方形的一组对边为直径作两个半圆，其余部分涂上阴影，则阴影部分的面积为______．

17．直角三角形的两条直角边长为6，8，那么斜边上的中线长是____．
18．如图是我市某连续7天的最高气温与最低气温的变化图，根据图中信息可知，这7天中最大的日温差是 ℃．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）如图，某校准备给长12米，宽8米的矩形室内场地进行地面装饰，现将其划分为区域Ⅰ（菱形），区域Ⅱ（4个全等的直角三角形），剩余空白部分记为区域Ⅲ；点为矩形和菱形的对称中心，，，，为了美观，要求区域Ⅱ的面积不超过矩形面积的，若设米.


甲
乙
丙
单价（元/米2）



（1）当时，求区域Ⅱ的面积.计划在区域Ⅰ，Ⅱ分别铺设甲，乙两款不同的深色瓷砖，区域Ⅲ铺设丙款白色瓷砖，
①在相同光照条件下，当场地内白色区域的面积越大，室内光线亮度越好.当为多少时，室内光线亮度最好，并求此时白色区域的面积.
②三种瓷砖的单价列表如下，均为正整数，若当米时，购买三款瓷砖的总费用最少，且最少费用为7200元，此时__________，__________.
20．（6分）如图1，2分别是某款篮球架的实物图与示意图，已知底座BC的长为0.60m，底座BC与支架AC所成的角∠ACB=75°，点A、H、F在同一条直线上，支架AH段的长为1m，HF段的长为1.50m，篮板底部支架HE的长为0.75m．求篮板底部支架HE与支架AF所成的角∠FHE的度数．求篮板顶端F到地面的距离．(结果精确到0.1 m；参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，≈1.732，≈1.414)

21．（6分）如图，∠BAO=90°，AB=8，动点P在射线AO上，以PA为半径的半圆P交射线AO于另一点C，CD∥BP交半圆P于另一点D，BE∥AO交射线PD于点E，EF⊥AO于点F，连接BD，设AP=m．
（1）求证：∠BDP=90°．
（2）若m=4，求BE的长．
（3）在点P的整个运动过程中．
①当AF=3CF时，求出所有符合条件的m的值．
②当tan∠DBE=时，直接写出△CDP与△BDP面积比．

22．（8分）已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F. 求证：BE=DF.
23．（8分）为响应“植树造林、造福后人”的号召，某班组织部分同学义务植树棵，由于同学们的积极参与，实际参加的人数比原计划增加了，结果每人比原计划少栽了棵，问实际有多少人参加了这次植树活动？
24．（10分）计算:.
25．（10分）在△ABC中，已知AB=AC，∠BAC=90°，E为边AC上一点，连接BE．
(1)如图1，若∠ABE=15°，O为BE中点，连接AO，且AO=1，求BC的长；
(2)如图2，D为AB上一点，且满足AE=AD，过点A作AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M，求证：BG=AF+FG．

26．（12分）对于某一函数给出如下定义：若存在实数m，当其自变量的值为m时，其函数值等于﹣m，则称﹣m为这个函数的反向值．在函数存在反向值时，该函数的最大反向值与最小反向值之差n称为这个函数的反向距离．特别地，当函数只有一个反向值时，其反向距离n为零．
例如，图中的函数有4，﹣1两个反向值，其反向距离n等于1．
（1）分别判断函数y＝﹣x+1，y＝，y＝x2有没有反向值？如果有，直接写出其反向距离；
（2）对于函数y＝x2﹣b2x，
①若其反向距离为零，求b的值；
②若﹣1≤b≤3，求其反向距离n的取值范围；
（3）若函数y＝请直接写出这个函数的反向距离的所有可能值，并写出相应m的取值范围．

27．（12分）校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载，某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于24米，在l上点D的同侧取点A、B，使∠CAD＝30°，∠CBD＝60°．求AB的长（结果保留根号）；已知本路段对校车限速为45千米/小时，若测得某辆校车从A到B用时1.5秒，这辆校车是否超速？说明理由．（参考数据：≈1.7，≈1.4）




参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、D
【解析】
∵∠ACD对的弧是，对的另一个圆周角是∠ABD，
∴∠ABD=∠ACD（同圆中，同弧所对的圆周角相等），
又∵AB为直径，
∴∠ADB=90°，
∴∠ABD+∠BAD=90°，
即∠ACD+∠BAD=90°，
∴与∠ACD互余的角是∠BAD.
故选D.
2、B
【解析】
根据反比例函数的性质得k＞0，然后根据一次函数的进行判断直线y=kx-k不经过的象限．
【详解】
∵反比例函数y=的图象在一、三象限，
∴k＞0，
∴直线y=kx﹣k经过第一、三、四象限，即不经过第二象限．
故选：B．
【点睛】
考查了待定系数法求反比例函数的解析式：设出含有待定系数的反比例函数解析式y=（k为常数，k≠0）；把已知条件（自变量与函数的对应值）代入解析式，得到待定系数的方程；解方程，求出待定系数；写出解析式．也考查了反比例函数与一次函数的性质．
3、D
【解析】
①错误．由题意a＞1．b＞1，c＜1，abc＜1；
②正确．因为y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，当ax2+bx+c＜mx+n时，-3＜x＜-1；即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确；
③错误．抛物线与x轴的另一个交点是（1，1）；
④正确．抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
【详解】
解：∵抛物线开口向上，∴a＞1，
∵抛物线交y轴于负半轴，∴c＜1，
∵对称轴在y轴左边，∴- ＜1，
∴b＞1，
∴abc＜1，故①错误．
∵y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，
当ax2+bx+c＜mx+n时，-3＜x＜-1；
即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确，
抛物线与x轴的另一个交点是（1，1），故③错误，
∵抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，
∴方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
故选：D．
【点睛】
本题考查二次函数的性质、二次函数与不等式，二次函数与一元二次方程等知识，解题的关键是灵活运用所学知识解决问题，学会利用数形结合的思想解决问题．
4、D
【解析】
∵函数的图象过点A（1，m），B（4，n），
∴m==，n==3，
∴A（1，），B（4，3），
过A作AC∥x轴，交B′B的延长线于点C，则C（4，），
∴AC=4﹣1=3，
∵曲线段AB扫过的面积为9（图中的阴影部分），
∴AC•AA′=3AA′=9，
∴AA′=3，即将函数的图象沿y轴向上平移3个单位长度得到一条新函数的图象，
∴新图象的函数表达式是．
故选D．

5、C
【解析】
由平面图形的折叠及正方形的展开图结合本题选项，一一求证解题.
【详解】
解：A、B、D都是正方体的展开图，故选项错误；
C、带“田”字格，由正方体的展开图的特征可知，不是正方体的展开图．
故选C．
【点睛】
此题考查正方形的展开图，难度不大，但是需要空间想象力才能更好的解题
6、B
【解析】
A、将此图形绕任意点旋转180度都不能与原图重合，所以这个图形不是中心对称图形.
【详解】
A、将此图形绕任意点旋转180度都不能与原图重合，所以这个图形不是中心对称图形;
B、将此图形绕中心点旋转180度与原图重合，所以这个图形是中心对称图形;
C、将此图形绕任意点旋转180度都不能与原图重合，所以这个图形不是中心对称图形;
D、将此图形绕任意点旋转180度都不能与原图重合，所以这个图形不是中心对称图形．
故选B.
【点睛】
本题考查了轴对称与中心对称图形的概念：
中心对称图形是要寻找对称中心，旋转180度后与原图重合.
7、C
【解析】
由方程有两个相等的实数根，得到根的判别式等于0，求出m的值，经检验即可得到满足题意m的值．
【详解】
∵一元二次方程mx1+mx﹣＝0有两个相等实数根，
∴△＝m1﹣4m×（﹣）＝m1+1m＝0，
解得：m＝0或m＝﹣1，
经检验m＝0不合题意，
则m＝﹣1．
故选C．
【点睛】
此题考查了根的判别式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．
8、A
【解析】
∵在Rt△ABC中,∠C=90°，AB=4，AC=1，
∴BC== ，
则cosB== ，
故选A
9、B
【解析】
利用三角形内角与外角的关系：三角形的任一外角等于和它不相邻的两个内角之和解答．
【详解】
如图，

∵∠1、∠2是△CDE的外角，
∴∠1=∠4+∠C，∠2=∠3+∠C，
即∠1+∠2=2∠C+（∠3+∠4），
∵∠3+∠4=180°-∠C=90°，
∴∠1+∠2=2×90°+90°=270°．
故选B．
【点睛】
此题主要考查了三角形内角与外角的关系：三角形的任一外角等于和它不相邻的两个内角之和．
10、C
【解析】
分析：
由题意易得当﹣3＜x＜﹣2时，函数的图象位于第二象限，且y随x的增大而增大，再计算出当x=-3和x=-2时对应的函数值，即可作出判断了.
详解：
∵在中，﹣6＜0，
∴当﹣3＜x＜﹣2时函数的图象位于第二象限内，且y随x的增大而增大，
∵当x=﹣3时，y=2，当x=﹣2时，y=3，
∴当﹣3＜x＜﹣2时，2＜y＜3，
故选C．
点睛：熟悉“反比例函数的图象和性质”是正确解答本题的关键.
11、A
【解析】
解：①有理数与无理数的和一定是有理数，故本小题错误；
②有理数与无理数的和一定是无理数，故本小题正确；
③例如=0，0是有理数，故本小题错误；
④例如（﹣）×=﹣2，﹣2是有理数，故本小题错误．
故选A．
点睛：本题考查的是实数的运算及无理数、有理数的定义，熟知以上知识是解答此题的关键．
12、D
【解析】
过点C作CD⊥x轴与D，如图，先利用一次函数图像上点的坐标特征确定B（0,2），A（1,0），再证明△ABO≌△CAD，得到AD＝OB＝2，CD＝AO＝1，则C点坐标可求.
【详解】
如图，过点C作CD⊥x轴与D.∵函数y=﹣2x+2的图象分别与x轴，y轴交于A，B两点，∴当x＝0时，y＝2，则B（0,2）；当y＝0时，x＝1，则A（1,0）.∵AC⊥AB，AC＝AB，∴∠BAO＋∠CAD＝90°，∴∠ABO＝∠CAD.在△ABO和△CAD中，，∴△ABO≌△CAD，∴AD＝OB＝2，CD＝OA＝1，∴OD＝OA＋AD＝1＋2＝3，∴C点坐标为（3,1）.故选D.

【点睛】
本题主要考查一次函数的基本概念。角角边定理、全等三角形的性质以及一次函数的应用，熟练掌握相关知识点是解答的关键.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、
【解析】
坡度=坡角的正切值，据此直接解答．
【详解】
解：∵，
∴坡角=30°．
【点睛】
此题主要考查学生对坡度及坡角的理解及掌握．
14、x＜－1
【解析】

解不等式①得:x<5,
解不等式②得:x<-1
所以不等式组的解集是x<-1.
故答案是:x<-1.
15、2
【解析】
直接利用接近和的数据得出符合题意的答案.
【详解】
解：到之间可以为：2（答案不唯一），
故答案为：2（答案不唯一）．
【点睛】
此题考查无理数的估算，解题的关键在于利用题中所给有理数的大小求符合题意的答案.
16、4﹣π
【解析】
由题意可以假设A（-m，m），则-m2=-4，求出点A坐标即可解决问题.
【详解】
由题意可以假设A（-m，m），
则-m2=-4，
∴m=≠±2，
∴m=2，
∴S阴=S正方形-S圆=4-π，
故答案为4-π．
【点睛】
本题考查反比例函数图象上的点的特征、正方形的性质、圆的面积公式等知识，解题的关键是灵活运用所学知识解决问题
17、1．
【解析】
试题分析：∵直角三角形的两条直角边长为6，8，∴由勾股定理得，斜边=10.
∴斜边上的中线长=×10=1．
考点：1.勾股定理；2. 直角三角形斜边上的中线性质．
18、11.
【解析】
试题解析：∵由折线统计图可知，周一的日温差=8℃+1℃=9℃；周二的日温差=7℃+1℃=8℃；周三的日温差=8℃+1℃=9℃；周四的日温差=9℃；周五的日温差=13℃﹣5℃=8℃；周六的日温差=15℃﹣71℃=8℃；周日的日温差=16℃﹣5℃=11℃，
∴这7天中最大的日温差是11℃．
考点：1.有理数大小比较；2.有理数的减法．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）8m2;（2）68m2;(3) 40，8
【解析】
（1）根据中心对称图形性质和,,,可得,即可解当时，4个全等直角三角形的面积；
（2）白色区域面积即是矩形面积减去一二部分的面积，分别用含x的代数式表示出菱形和四个全等直角三角形的面积，列出含有x的解析式表示白色区域面积，并化成顶点式，根据，，，求出自变量的取值范围，再根据二次函数的增减性即可解答；
（3）计算出x=2时各部分面积以及用含m、n的代数式表示出费用，因为m,n均为正整数，解得m=40，n=8.
【详解】
（1） ∵为长方形和菱形的对称中心，，∴
∵，，∴
∴当时，，
（2）∵，
∴-，
∵，，
∴解不等式组得，
∵，结合图像，当时，随的增大而减小.
∴当时， 取得最大值为
（3）∵当时，SⅠ=4x2=16 m2，=12 m2，=68m2，总费用:16×2m+12×5n+68×2m=7200,化简得：5n+14m=600,因为m,n均为正整数，解得m=40，n=8.
【点睛】
本题考查中心对称图形性质，菱形、直角三角形的面积计算，二次函数的最值问题，解题关键是用含x的二次函数解析式表示出白色区面积.
20、（1）∠FHE＝60°；（2）篮板顶端 F 到地面的距离是 4.4 米．
【解析】
（1）直接利用锐角三角函数关系得出cos∠FHE=，进而得出答案；
（2）延长FE交CB的延长线于M，过A作AG⊥FM于G，解直角三角形即可得到结论．
【详解】
（1 ）由题意可得：cos∠FHE＝，则∠FHE＝60°；
（2）延长 FE 交 CB 的延长线于 M，过 A 作 AG⊥FM 于 G，

在 Rt△ABC 中，tan∠ACB＝，
∴AB＝BC•tan75°＝0.60×3.732＝2.2392，
∴GM＝AB＝2.2392，
在 Rt△AGF 中，∵∠FAG＝∠FHE＝60°，sin∠FAG＝，
∴sin60°＝＝，
∴FG≈2.17（m），
∴FM＝FG+GM≈4.4（米），
答：篮板顶端 F 到地面的距离是 4.4 米．
【点睛】
本题考查解直角三角形、锐角三角函数、解题的关键是添加辅助线，构造直角三角形，记住锐角三角函数的定义.
21、（1）详见解析；（2）的长为1；（3）m的值为或；与面积比为或．
【解析】
由知，再由知、，据此可得，证≌即可得；
易知四边形ABEF是矩形，设，可得，证≌得，在中，由，列方程求解可得答案；
分点C在AF的左侧和右侧两种情况求解：左侧时由知、、，在中，由可得关于m的方程，解之可得；右侧时，由知、、，利用勾股定理求解可得．作于点G，延长GD交BE于点H，由≌知，据此可得，再分点D在矩形内部和外部的情况求解可得．
【详解】
如图1，

，
，
，
、，
，
，
≌，
．
，，
，
，
，
四边形ABEF是矩形，
设，则，
，
，
，
，
≌，
，
≌，
，
在中，，即，
解得：，
的长为1．
如图1，当点C在AF的左侧时，
，则，
，
，，
在中，由可得，
解得：负值舍去；
如图2，当点C在AF的右侧时，

，
，
，
，，
在中，由可得，
解得：负值舍去；
综上，m的值为或；
如图3，过点D作于点G，延长GD交BE于点H，

≌，
，
又，且，
，
当点D在矩形ABEF的内部时，
由可设、，
则，
，
则；
如图4，当点D在矩形ABEF的外部时，

由可设、，
则，
，
则，
综上，与面积比为或．
【点睛】
本题考查了四边形的综合问题，解题的关键是掌握矩形的判定与性质、全等三角形的判定和性质及勾股定理、三角形的面积等知识点．
22、（1）证明：∵ABCD是平行四边形
∴AB=CD
AB∥CD
∴∠ABE=∠CDF
又∵AE⊥BD，CF⊥BD
∴∠AEB=∠CFD=
∴△ABE≌△CDF
∴BE=DF
【解析】
证明:在□ABCD中
∵AB∥CD
∴∠ABE=∠CDF…………………………………………………………4分
∵AE⊥BD CF⊥BD
∴∠AEB=∠CFD=900……………………………………………………5分
∵AB=CD
∴△ABE≌△CDF…………………………………………………………6分
∴BE=DF
23、人
【解析】
解：设原计划有x人参加了这次植树活动
依题意得：
解得 x=30人
经检验x=30是原方程式的根
实际参加了这次植树活动1.5x=45人
答实际有45人参加了这次植树活动．
24、
【解析】
【分析】括号内先进行通分，进行分式的加减法运算，然后再与括号外的分式进行分式乘除法运算即可.
【详解】原式=
=
=.
【点睛】本题考查了分式的混合运算，熟练掌握有关分式的运算法则是解题的关键.
25、（1） （2）证明见解析
【解析】
（1）如图1中，在AB上取一点M，使得BM=ME，连接ME．，设AE=x，则ME=BM=2x，AM=x，根据AB2+AE2=BE2，可得方程（2x+x）2+x2=22，解方程即可解决问题．
（2）如图2中，作CQ⊥AC，交AF的延长线于Q，首先证明EG=MG，再证明FM=FQ即可解决问题．
【详解】
解：如图 1 中，在 AB 上取一点 M，使得 BM=ME，连接 ME．
在 Rt△ABE 中，∵OB=OE，
∴BE=2OA=2，
∵MB=ME，
∴∠MBE=∠MEB=15°，
∴∠AME=∠MBE+∠MEB=30°，设 AE=x，则 ME=BM=2x，AM=x，
∵AB2+AE2=BE2，
∴，
∴x= （负根已经舍弃），
∴AB=AC=（2+ ）• ，
∴BC= AB= +1．
作 CQ⊥AC，交 AF 的延长线于 Q，

∵ AD=AE ，AB=AC ，∠BAE=∠CAD，
∴△ABE≌△ACD（SAS），
∴∠ABE=∠ACD，
∵∠BAC=90°，FG⊥CD，
∴∠AEB=∠CMF，
∴∠GEM=∠GME，
∴EG=MG，
∵∠ABE=∠CAQ，AB=AC，∠BAE=∠ACQ=90°，
∴△ABE≌△CAQ（ASA），
∴BE=AQ，∠AEB=∠Q，
∴∠CMF=∠Q，
∵∠MCF=∠QCF=45°，CF=CF，
∴△CMF≌△CQF（AAS），
∴FM=FQ，
∴BE=AQ=AF+FQ=AF=FM，
∵EG=MG，
∴BG=BE+EG=AF+FM+MG=AF+FG．
【点睛】
本题考查全等三角形的判定和性质、直角三角形斜边中线定理，等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
26、（1）y＝−有反向值，反向距离为2；y＝x2有反向值，反向距离是1；（2）①b＝±1；②0≤n≤8；（3）当m＞2或m≤﹣2时，n＝2，当﹣2＜m≤2时，n＝2．
【解析】
(1)根据题目中的新定义可以分别计算出各个函数是否有方向值，有反向值的可以求出相应的反向距离；
(2)①根据题意可以求得相应的b的值；
②根据题意和b的取值范围可以求得相应的n的取值范围；
(3)根据题目中的函数解析式和题意可以解答本题．
【详解】
(1)由题意可得，
当﹣m＝﹣m+1时，该方程无解，故函数y＝﹣x+1没有反向值，
当﹣m＝时，m＝±1，∴n＝1﹣(﹣1)＝2，故y＝有反向值，反向距离为2，
当﹣m＝m2，得m＝0或m＝﹣1，∴n＝0﹣(﹣1)＝1，故y＝x2有反向值，反向距离是1；
(2)①令﹣m＝m2﹣b2m，
解得，m＝0或m＝b2﹣1，
∵反向距离为零，
∴|b2﹣1﹣0|＝0，
解得，b＝±1；
②令﹣m＝m2﹣b2m，
解得，m＝0或m＝b2﹣1，
∴n＝|b2﹣1﹣0|＝|b2﹣1|，
∵﹣1≤b≤3，
∴0≤n≤8；
(3)∵y＝，
∴当x≥m时，
﹣m＝m2﹣3m，得m＝0或m＝2，
∴n＝2﹣0＝2，
∴m＞2或m≤﹣2；
当x＜m时，
﹣m＝﹣m2﹣3m，
解得，m＝0或m＝﹣2，
∴n＝0﹣(﹣2)＝2，
∴﹣2＜m≤2，
由上可得，当m＞2或m≤﹣2时，n＝2，
当﹣2＜m≤2时，n＝2．
【点睛】
本题是一道二次函数综合题，解答本题的关键是明确题目中的新定义，找出所求问题需要的条件，利用新定义解答相关问题．
27、 (1) ;(2)此校车在AB路段超速，理由见解析.
【解析】
（1）结合三角函数的计算公式，列出等式，分别计算AD和BD的长度，计算结果，即可．（2）在第一问的基础上，结合时间关系，计算速度，判断，即可．
【详解】
解：（1）由题意得，在Rt△ADC中，tan30°＝＝，
解得AD＝24．
在 Rt△BDC 中，tan60°＝＝，
解得BD＝8
所以AB＝AD﹣BD＝24﹣8＝16（米）．
（2）汽车从A到B用时1.5秒，所以速度为16÷1.5≈18.1（米/秒），
因为18.1（米/秒）＝65.2千米/时＞45千米/时，
所以此校车在AB路段超速．
【点睛】
考查三角函数计算公式，考查速度计算方法，关键利用正切值计算方法，计算结果，难度中等．