

甘肃省陇南市武都区2021--2022学年八年级下学期数学期末测试模拟卷(含答案)
展开一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 下列各式无意义的是( )
A.-5B.10-4C.-15D.(-5)2
2. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5B.6C.7D.25
3. 下列说法中,错误的是( )
A.平行四边形的对角线互相平分
B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直
D.对角线互相垂直的四边形是菱形
4. 下列式子中,二次根式的个数是( )
①3a2+3;②39;③-22+2;④0.16;⑤3-2.
A.1B.2C.3D.4
5. 我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是16,小正方形的面积是3,直角三角形较短的直角边为a,较长的直角边为b那么(a+b)2的值为( )
A.16B.29C.19D.48
6. 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于( )
A.1:2B.1:3C.1:4D.1:5
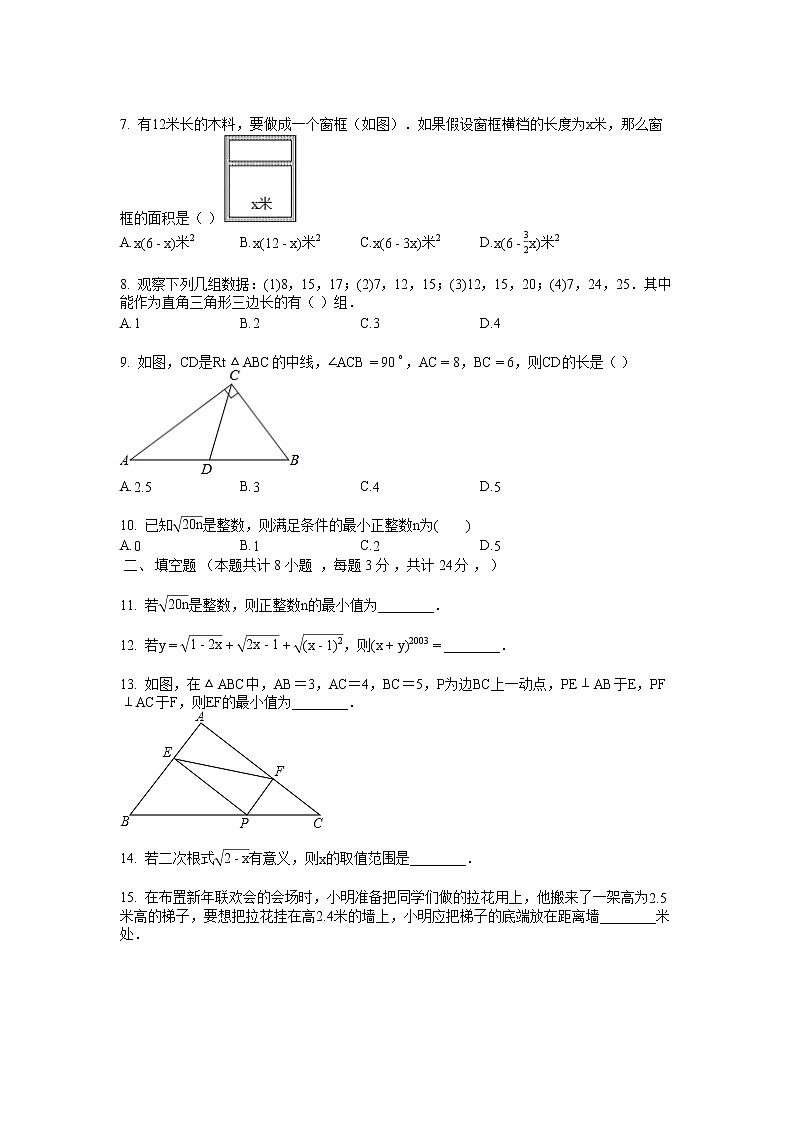
7. 有12米长的木料,要做成一个窗框(如图).如果假设窗框横档的长度为x米,那么窗框的面积是( )
A.x(6-x)米2B.x(12-x)米2C.x(6-3x)米2D.x(6-32x)米2
8. 观察下列几组数据:(1)8,15,17;(2)7,12,15;(3)12,15,20;(4)7,24,25.其中能作为直角三角形三边长的有( )组.
A.1B.2C.3D.4
9. 如图,CD是Rt△ABC的中线,∠ACB=90∘,AC=8,BC=6,则CD的长是( )
A.2.5B.3C.4D.5
10. 已知20n是整数,则满足条件的最小正整数n为( )
A.0B.1C.2D.5
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
11. 若20n是整数,则正整数n的最小值为________.
12. 若y=1-2x+2x-1+(x-1)2,则(x+y)2003=________.
13. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为________.
14. 若二次根式2-x有意义,则x的取值范围是________.
15. 在布置新年联欢会的会场时,小明准备把同学们做的拉花用上,他搬来了一架高为2.5米高的梯子,要想把拉花挂在高2.4米的墙上,小明应把梯子的底端放在距离墙________米处.
16. 在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则该菱形的面积为________.
17. 观察下列等式:
1+112+122=1+11-11+1=1121+122+132=1+12-12+1=1161+132+142=1+13-13+1=1112
…
请你根据以上规律,写出第n个等式________.
18. 如图,点O是▱ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=12AB;G,H是BC边上的点,且GH=13BC.用S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是________.
三、 解答题 (本题共计 10 小题 ,共计96分 , )
19. (10分) 已知x、y为实数,y=x2-9+9-x2+1x-3,求5x+6y的值.
20. (10分) (1)观察发现:
如图(1),已知直线m // n,点A、B在直线n上,点C、P在直线m上,当点P在直线m上移动到任意一位置时,总有________与△ABC的面积相等. 20. (10分)
(2)实践应用
①如图(2),在△ABC中,已知BC=6,且BC边上的高为5,若过C作CE // AB,连接AE,BE,则△BAE的面积=________;
②如图(3),A、B、E三点在同一直线上,四边形ABCD和四边形BEFG都是邻边相等的平行四边形,若AB=5,AC=4,求△ACF的面积.
20. (10分)
(3)拓展延伸
如图(4),在四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC
21.(10分) 如图:已知:AD是△ABC的角平分线,DE // AC交AB于E,DF // AB交AC于F.
(1)求证:四边形AEDF是菱形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形?
22. (10分) 计算:25+125-15145.
23. (10分) 如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
24.(10分) 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BF=DE.
(1)四边形AECF是什么样的特殊四边形?请说明理由;
(2)若AB=2,BF=22,求四边形AECF的面积.
25.(9分) 研究发现,地表以下岩层的温度与它所处的深度有表中的关系:
根据以上信息,回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)岩层的深度h每增加1km,温度t是怎样变化的?
(3)估计岩层10km深处的温度是多少?
26.(9分) 计算:
(1)8-212
(2)(32-2)2
(3)20+1255+5
(4)(32+13)×3-2163.
27. (9分) 如图,在▱ABCD中,对角线AC,BD交于点O,点E,F分别是AB,BC的中点,EF交BD于G,连接OE,OF.求证:线段OB与线段EF相互平分.
28. (9分) 如图,在正方形ABCD中,E是BC延长线上一点,且AC=EC,求∠DAE的度数.
参考答案与试题解析
2022年春季学期八年级数学期末测试模拟卷
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【考点】
二次根式有意义的条件
【解析】
根据二次根式有意义的条件:被开方数是非负数即可判断.
【解答】
解:A,∵ 5>0,∴ -5有意义,故A不符合题意;
B,∵ 10-4=1104>0,∴ 10-4有意义,故B不符合题意;
C,∵ -15<0,∴ -15无意义,故C符合题意;
D,∵ (-5)2=25>0,∴ (-5)2有意义,故D不符合题意;
故选C.
2.
【答案】
A
【考点】
勾股定理
【解析】
建立格点三角形,利用勾股定理求解AB的长度即可.
【解答】
解:如图所示:
AB=AC2+BC2=5.
故选:A.
3.
【答案】
D
【考点】
菱形的判定与性质
平行四边形的应用
【解析】
根据平行四边形和菱形的性质对各个选项进行分析从而得到最后答案.
【解答】
解:根据平行四边形和菱形的性质得到ABC均正确,而D不正确,因为对角线互相垂直的四边形也可能是梯形,
故选:D.
4.
【答案】
C
【考点】
二次根式的定义及识别
【解析】
确定根指数为2,被开方数为非负数的根式即可.注意3-2=19.
【解答】
解:①④⑤符合二次根式的定义,是二次根式;
②根指数为3,不是二次根式;③-22=-4<0,-22无意义,不是二次根式.
故选C.
5.
【答案】
B
【考点】
勾股定理的证明
【解析】
易求得ab的值,和a2+b2的值,根据完全平方公式即可求得(a+b)2的值,即可解题.
【解答】
∵ 大正方形的面积是16,小正方形的面积是3,
∴ 四个直角三角形面积和为16-3=13,即4×12ab=13,
∴ 2ab=13,a2+b2=16,
∴ (a+b)2=a2+b2+2ab=16+13=29.
答:(a+b)2的值为29,
故选:B.
6.
【答案】
B
【考点】
三角形中位线定理
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半,可以求出DE=12BC,又点M是DE的中点,可以求出DM:BC的值,也就等于MN:NC的值,从而可以得到MN:MC的比值,也就是点N到DE的距离与点C到DE的距离之比,又DM=ME,所以S△DMN:S△CEM=MN:MC.
【解答】
解:∵ DE是△ABC的中位线,
∴ DE // BC,DE=12BC,
∵ M是DE的中点,
∴ DM=ME=14BC,
∴ MNNC=DMBC=14,
∴ MNMC=NFCG=13,
即:点N到DE的距离与点C到DE的距离之比为13,
∵ DM=ME,
∴ S△DMN:S△CEM=1:3.
故选B.
(根据虚线可以看出两三角形的边DM、ME上的高的比等于MN:MC)
7.
【答案】
D
【考点】
列代数式
【解析】
横档的长度为x米,则竖档的长度=(12-3x)÷2=6-1.5x,根据窗框的面积=长×宽求出答案.
【解答】
解:竖档的长度=(12-3x)÷2=6-1.5x,
∴ 窗框的面积=长×宽
=x(6-1.5x)
=x(6-32x)米2.
故选D.
8.
【答案】
B
【考点】
勾股定理的逆定理
【解析】
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
【解答】
解:①82+152=172,根据勾股定理的逆定理是直角三角形,故正确;
②72+122≠152,根据勾股定理的逆定理不是直角三角形,故错误;
③122+152≠202,根据勾股定理的逆定理不是直角三角形,故错误;
④72+242=252,根据勾股定理的逆定理是直角三角形,故正确.
故选B.
9.
【答案】
D
【考点】
直角三角形斜边上的中线
勾股定理
【解析】
利用勾股定理列式求出AB,再根据直角三角形斜边上的中线等于斜边的一半解答.
【解答】
解:∵ ∠ACB=90∘,AC=8,BC=6,
∴ AB=AC2+BC2=82+62=10,
∵ CD是Rt△ABC的中线,
∴ CD=12AB=12×10=5.
故选D.
10.
【答案】
D
【考点】
二次根式的定义及识别
【解析】
首先化简二次根式进而得出n的最小值.
【解答】
解:∵ 20n=25n是整数,
∴ 满足条件的最小正整数n为5.
故选D.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
5
【考点】
二次根式的定义及识别
【解析】
20n是正整数,则20n一定是一个完全平方数,首先把20n分解因数,确定20n是完全平方数时,n的最小值即可.
【解答】
解:∵ 20n=22×5n.
∴ 正整数n的最小值为5.
故答案为:5.
12.
【答案】
1
【考点】
二次根式的性质与化简
二次根式有意义的条件
【解析】
根据二次根式有意义的条件可以求出x、y的值,代入所求代数式计算即可.
【解答】
解:∵ y=1-2x+2x-1+(x-1)2,
∴ 1-2x≥0且2x-1≥0,综合得x=12;
∴ y=1-2x+2x-1+(x-1)2=0+0+12=12,
∴ (x+y)2003=(12+12)2003=1.
故答案为:1.
13.
【答案】
2.4
【考点】
垂线段最短
矩形的判定与性质
【解析】
根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
【解答】
连接AP,
∵ 在△ABC中,AB=3,AC=4,BC=5,
∴ AB2+AC2=BC2,
即∠BAC=90∘.
又∵ PE⊥AB于E,PF⊥AC于F,
∴ 四边形AEPF是矩形,
∴ EF=AP,
∵ AP的最小值即为直角三角形ABC斜边上的高,即2.4,
∴ EF的最小值为2.4,
14.
【答案】
x≤2
【考点】
二次根式有意义的条件
【解析】
根据被开方数大于等于0列式计算即可得解.
【解答】
解:由题意得,2-x≥0,
解得x≤2.
故答案为:x≤2.
15.
【答案】
0.7
【考点】
勾股定理的应用
【解析】
根据题意画出图形构造出直角三角形,再利用勾股定理解答即可.
【解答】
解:如图,AB=2.5m,AC=2.4m,
由勾股定理得,BC=AB2-AC2=2.52-2.42=0.7m.
16.
【答案】
12
【考点】
菱形的性质
【解析】
如图,根据菱形的性质,已知AC,BD的长,然后根据菱形的面积公式可求解.
【解答】
读图可知,AC=4,BD=6,则该菱形的面积为4×6×12=12.
17.
【答案】
1+1n2+1(n+1)2=1+1n-1n+1=1+1n(n+1)
【考点】
二次根式的性质与化简
【解析】
根据已知算式得出规律,根据规律求出即可.
【解答】
∵ 观察下列等式:
1+112+122=1+11-11+1=1121+122+132=1+12-12+1=1161+132+142=1+13-13+1=1112
…
∴ 第n个等式是1+1n2+1(n+1)2=1+1n-1n+1=1+1n(n+1),
18.
【答案】
S1S2=32
【考点】
三角形的面积
中心对称
平行四边形的性质
【解析】
本题考查了中心对称,三角形的面积,平行四边形的性质.
【解答】
解:∵ S1S△AOB=EFAB=12,S2S△BOC=GHBC=13,
∴ S1=12S△AOB,S2=13S△BOC.
∵ 点O是▱ABCD的对称中心,
∴ S△AOB=S△BOC=14S▱ABCD,
∴ S1S2=1213=32.
即S1与S2之间的等量关系是S1S2=32.
故答案为:S1S2=32.
三、 解答题 (本题共计 10 小题 ,共计96分 )
19.
【答案】
解:∵ x2-9≥0,9-x2≥0,且x-3≠0,
∴ x=-3;
∴ y=-16.
∴ 5x+6y=5×(-3)+6×(-16)=-16,即5x+6y=-16.
【考点】
二次根式有意义的条件
【解析】
根据二次根式有意义的条件列出关于x的方程,求得x的值后,将其代入原式求得y值;最后将x、y值代入所求的代数式并求值即可.
【解答】
解:∵ x2-9≥0,9-x2≥0,且x-3≠0,
∴ x=-3;
∴ y=-16.
∴ 5x+6y=5×(-3)+6×(-16)=-16,即5x+6y=-16.
20.
【答案】
△APB;
(2)①如图(2),∵ 在△ABC中,已知BC=6,且BC边上的高为5,
∴ S△ABC=12×6×5=15.
又∵ CE // AB,
∴ △ABC与△BAE是同底等高的两个三角形.
S△BAE=S△ABC=15;
故答案是:15;
②如图(3),过点B作BH⊥AC于点H,连接BF.
∵ AB=BC,
∴ AH=12AC=2.
在直角△AHB中,BH=AB2-AH2=52-22=21.
∴ S△ABC=12×2×21=21.
∵ 四边形ABCD和四边形BEFG都是邻边相等的平行四边形,
∴ AC // BF,
∴ S△ACF=S△ABC=21.
(3)如图所示.
过点B作BE // AC交DC的延长线于点E,连接AE.
∵ BE // AC,
∴ △ABC和△AEC的公共边AC上的高也相等,
∴ 有S△ABC=S△AEC,
∴ S四边形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED;
∵ S△ACD>S△ABC,
所以面积等分线必与CD相交,取DE中点F,则直线AF即为要求作的四边形ABCD的面积等分线.
【考点】
平行线之间的距离
平行四边形的性质
【解析】
(1)由已知图形可以看出只有△APB与△ABC是同底等高的三角形.
(2)①△ABC与△BAE是同底等高的三角形.
②连接BF,先根据正方形的性质得出∠BAC=∠BFE,再由平行线的判定得出AC // BF,然后根据规律:同底等高的两个三角形面积相等,得出△ACF的面积等于△ABC的面积;
(3)如图(4),过点B作BE // AC交DC的延长线于点E,连接AE.根据“△ABC和△AEC的公共边AC上的高也相等”推知S△ABC=S△AEC;然后由“割补法”可以求得S四边形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED.
【解答】
解:(1)∵ 如图(1),直线m // n,
∴ △APB与△ABC是同底等高的三角形,
∴ S△APB=S△ABC;
(2)①如图(2),∵ 在△ABC中,已知BC=6,且BC边上的高为5,
∴ S△ABC=12×6×5=15.
又∵ CE // AB,
∴ △ABC与△BAE是同底等高的两个三角形.
S△BAE=S△ABC=15;
(3)如图所示.
过点B作BE // AC交DC的延长线于点E,连接AE.
∵ BE // AC,
∴ △ABC和△AEC的公共边AC上的高也相等,
∴ 有S△ABC=S△AEC,
∴ S四边形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED;
∵ S△ACD>S△ABC,
所以面积等分线必与CD相交,取DE中点F,则直线AF即为要求作的四边形ABCD的面积等分线.
21.
【答案】
解:(1)证明:∵ DE // AC,DF // AB,
∴ DE // AF,DF // AE,
∴ 四边形AEDF是平行四边形(有两组对边相互平行的四边形是平行四边形),
∴ ∠EAF=∠EDF(平行四边形的对角相等);
又∵ AD是△ABC的角平分线,
∴ ∠EAD=∠EDA(平行四边形的对角线平分对角),
∴ AE=DE(等角对等边),
∴ 四边形AEDF是菱形(邻边相等的平行四边形是菱形);
(2)由(1)知,四边形AEDF是菱形,
∵ 当四边形AEDF是正方形时,∠EAF=90∘,即∠BAC=90∘,
∴ △ABC的∠BAC=90∘时,四边形AEDF是正方形.
【考点】
正方形的判定与性质
菱形的判定
【解析】
(1)根据平行四边形的判定定理--有两组对边相互平行的四边形是平行四边形,推知四边形AEDF是平行四边形;然后由平行四边形的对角相等、对角线平分对角的性质以及角平分线的性质证得∠EAD=∠EDA;最后由等角对等边推知▱ABCD的邻边AE=DE;
(2)由正方形的四个角都是直角的性质知三角形ABC中∠BAC=90∘.
【解答】
解:(1)证明:∵ DE // AC,DF // AB,
∴ DE // AF,DF // AE,
∴ 四边形AEDF是平行四边形(有两组对边相互平行的四边形是平行四边形),
∴ ∠EAF=∠EDF(平行四边形的对角相等);
又∵ AD是△ABC的角平分线,
∴ ∠EAD=∠EDA(平行四边形的对角线平分对角),
∴ AE=DE(等角对等边),
∴ 四边形AEDF是菱形(邻边相等的平行四边形是菱形);
(2)由(1)知,四边形AEDF是菱形,
∵ 当四边形AEDF是正方形时,∠EAF=90∘,即∠BAC=90∘,
∴ △ABC的∠BAC=90∘时,四边形AEDF是正方形.
22.
【答案】
解:原式=25+55-5
=65.
【考点】
二次根式的相关运算
【解析】
先将二次根式化为最简,然后合并同类二次根式即可.
【解答】
解:原式=25+55-5
=65.
23.
【答案】
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD // BC,
∵ DE=BF,
∴ AE=CF,∵ AE // CF,
∴ 四边形AECF是平行四边形,
∵ AC⊥EF,
∴ 四边形AECF是菱形.
【考点】
菱形的判定
平行四边形的判定
平行四边形的性质
【解析】
根据对角线互相垂直的平行四边形是菱形即可证明;
【解答】
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD // BC,
∵ DE=BF,
∴ AE=CF,∵ AE // CF,
∴ 四边形AECF是平行四边形,
∵ AC⊥EF,
∴ 四边形AECF是菱形.
24.
【答案】
解:(1)四边形AECF为菱形;理由如下:
∵ 四边形ABCD为正方形,
∴ AC⊥BD,BO=DO,AO=CO;
∵ BF=DE,
∴ OF=OE,
∴ AC、EF互相垂直、平分,
∴ 四边形AECF为菱形.
(2)∵ 四边形ABCD为正方形,
∴ ∠ABC=90∘,AB=BC=2;
∴ AC2=22+22,
∴ BD=AC=22,EF=22-2×22=2,
∴ SAECF=12×22×2=2.
【考点】
正方形的性质
勾股定理
菱形的判定与性质
【解析】
(1)证明AC⊥EF,OA=OC,OE=OF即可解决问题.
(2)求出AC、EF的长度,运用菱形的性质即可解决问题.
【解答】
解:(1)四边形AECF为菱形;理由如下:
∵ 四边形ABCD为正方形,
∴ AC⊥BD,BO=DO,AO=CO;
∵ BF=DE,
∴ OF=OE,
∴ AC、EF互相垂直、平分,
∴ 四边形AECF为菱形.
(2)∵ 四边形ABCD为正方形,
∴ ∠ABC=90∘,AB=BC=2;
∴ AC2=22+22,
∴ BD=AC=22,EF=22-2×22=2,
∴ SAECF=12×22×2=2.
25.
【答案】
解:(1)上表反映了岩层的深度h(km)与岩层的温度t(∘C)之间的关系,
其中岩层深度h(km)是自变量,岩层的温度t(∘C)是因变量.
(2)岩层的深度h每增加1km,温度t上升35∘C.
(3)当h=10km时,t=35×(10-6)+230=370(∘C).
【考点】
自变量与因变量
列代数式求值
【解析】
(1)直接利用常量与变量的关系得出自变量和因变量;
(2)利用表格中数据进而得出答案;
(3)直接利用(2)中函数关系式得出t的值.
【解答】
解:(1)上表反映了岩层的深度h(km)与岩层的温度t(∘C)之间的关系,
其中岩层深度h(km)是自变量,岩层的温度t(∘C)是因变量.
(2)岩层的深度h每增加1km,温度t上升35∘C.
(3)当h=10km时,t=35×(10-6)+230=370(∘C).
26.
【答案】
解:(1)原式=22-2=2;
(2)原式=18-122+4=22-122;
(3)原式=25+555+5=7+5=12;
(4)原式=(42+33)×3-833=46+1-833.
【考点】
二次根式的混合运算
【解析】
(1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)利用完全平方公式计算;
(3)先把各二次根式化简为最简二次根式,然后进行二次根式的除法运算;
(4)先把各二次根式化简为最简二次根式,然后进行二次根式的乘法运算.
【解答】
解:(1)原式=22-2=2;
(2)原式=18-122+4=22-122;
(3)原式=25+555+5=7+5=12;
(4)原式=(42+33)×3-833=46+1-833.
27.
【答案】
解:点E,F分别是AB,BC的中点,
∴ OE是△ABC的中位线,且BF=12BC,
∴ OE=12BC,OE // BC,
∴ OE=BF,
∴ 四边形OEBF是平行四边形,
∴ 线段OB与线段EF相互平分.
【考点】
三角形中位线定理
平行四边形的性质与判定
【解析】
此题暂无解析
【解答】
解:点E,F分别是AB,BC的中点,
∴ OE是△ABC的中位线,且BF=12BC,
∴ OE=12BC,OE // BC,
∴ OE=BF,
∴ 四边形OEBF是平行四边形,
∴ 线段OB与线段EF相互平分.
28.
【答案】
解:∵ 四边形ABCD为正方形,
∴ ∠DAC=∠ACB=45∘,
∵ AC=CE,
∴ ∠E=∠EAC,
∵ 2∠EAC=∠E+∠EAC=∠ACB=45∘,
∴ ∠EAC=22.5∘,
∴ ∠DAE=∠DAC-∠EAC=45∘-22.5∘=22.5∘.
【考点】
正方形的性质
【解析】
根据正方形的对角线平分一组对角可得∠DAC=∠ACB=45∘,再根据等边对等角可得∠E=∠EAC,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠EAC,再根据∠DAE=∠DAC-∠EAC代入数据进行计算即可得解.
【解答】
解:∵ 四边形ABCD为正方形,
∴ ∠DAC=∠ACB=45∘,
∵ AC=CE,
∴ ∠E=∠EAC,
∵ 2∠EAC=∠E+∠EAC=∠ACB=45∘,
∴ ∠EAC=22.5∘,
∴ ∠DAE=∠DAC-∠EAC=45∘-22.5∘=22.5∘.岩层的深度h/km
1
2
3
4
5
6
⋯
岩层的温度t/∘C
55
90
125
160
195
230
⋯
2024年甘肃省陇南市武都区中考模拟预测数学试题: 这是一份2024年甘肃省陇南市武都区中考模拟预测数学试题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年甘肃省陇南市武都区中考模拟预测数学试题: 这是一份2024年甘肃省陇南市武都区中考模拟预测数学试题,共11页。
2024年甘肃省陇南市武都区九年级下学期联考模拟数学试题(原卷版+解析版): 这是一份2024年甘肃省陇南市武都区九年级下学期联考模拟数学试题(原卷版+解析版),文件包含2024年甘肃省陇南市武都区九年级下学期联考模拟数学试题原卷版docx、2024年甘肃省陇南市武都区九年级下学期联考模拟数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












