广西专用高考数学一轮复习第八章立体几何7立体几何中的向量方法课件新人教A版理

这是一份广西专用高考数学一轮复习第八章立体几何7立体几何中的向量方法课件新人教A版理，共60页。PPT课件主要包含了-2-，知识梳理，双基自测，e共线，垂直于，n⊥α，向量n，-3-，e2λe1，e1·e20等内容，欢迎下载使用。

1.直线的方向向量与平面的法向量(1)直线l上的非零向量e以及与　　　　　　的非零向量叫做直线l的方向向量. (2)如果表示非零向量n的有向线段所在直线　　　　　　平面α,那么称向量n垂直于平面α,记作　　　　.此时把　　　　　　叫做平面α的法向量. 
2.线面关系的判定设直线l1的方向向量为e1=(a1,b1,c1),直线l2的方向向量为e2=(a2,b2,c2),平面α的法向量为n1=(x1,y1,z1),平面β的法向量为n2=(x2,y2,z2).(1)如果l1∥l2,那么e1∥e2⇔　 　⇔　　　　　　　　　　. (2)如果l1⊥l2,那么e1⊥e2⇔　　　　　　⇔　　　　　　　　. (3)若l1∥α,则e1⊥n1⇔e1·n1=0⇔　　　　　　　　　　　　. (4)若l1⊥α,则e1∥n1⇔e1=μn1⇔　　　　　　　　　　　　. (5)若α∥β,则n1∥n2⇔n1=kn2⇔　　　　　　　　　　　　. (6)若α⊥β,则n1⊥n2⇔n1·n2=0⇔　　　　　　　　　　　　. 
a2=λa1,b2=λb1,c2=λc1
a1a2+b1b2+c1c2=0
a1x1+b1y1+c1z1=0
a1=μx1,b1=μy1,c1=μz1
x1=kx2,y1=ky2,z1=kz2
x1x2+y1y2+z1z2=0
3.利用空间向量求空间角(1)两条异面直线所成的角①范围:两条异面直线所成的角θ的取值范围是　　　　　　. ②向量求法:设异面直线a,b的方向向量为a,b,直线a与b的夹角为θ,a与b的夹角为φ,则有cs θ=　　　　. (2)直线与平面所成的角①范围:直线和平面所成的角θ的取值范围是　　　　　　. ②向量求法:设直线l的方向向量为a,平面的法向量为u,直线与平面所成的角为θ,a与u的夹角为φ,则有sin θ=　　　　或cs θ=sin φ. 
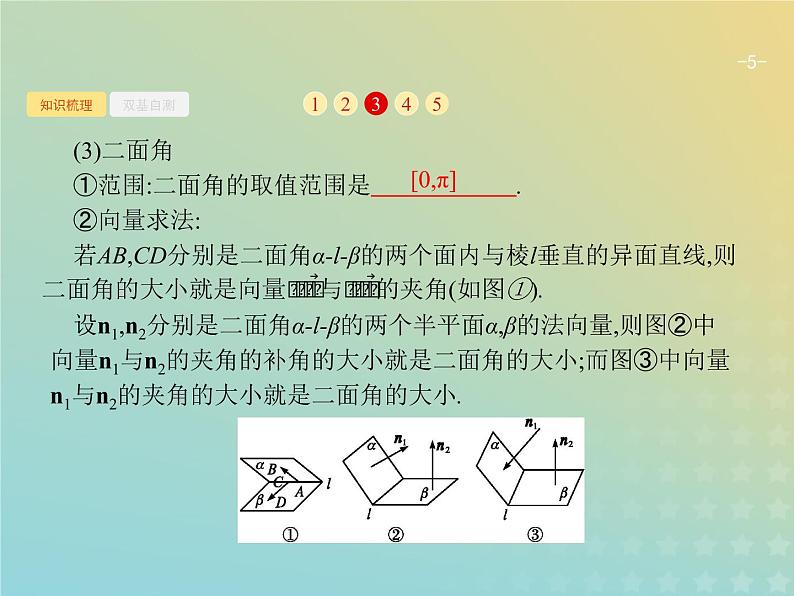
(3)二面角①范围:二面角的取值范围是　　　　　　. ②向量求法:若AB,CD分别是二面角α-l-β的两个面内与棱l垂直的异面直线,则设n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则图②中向量n1与n2的夹角的补角的大小就是二面角的大小;而图③中向量n1与n2的夹角的大小就是二面角的大小.
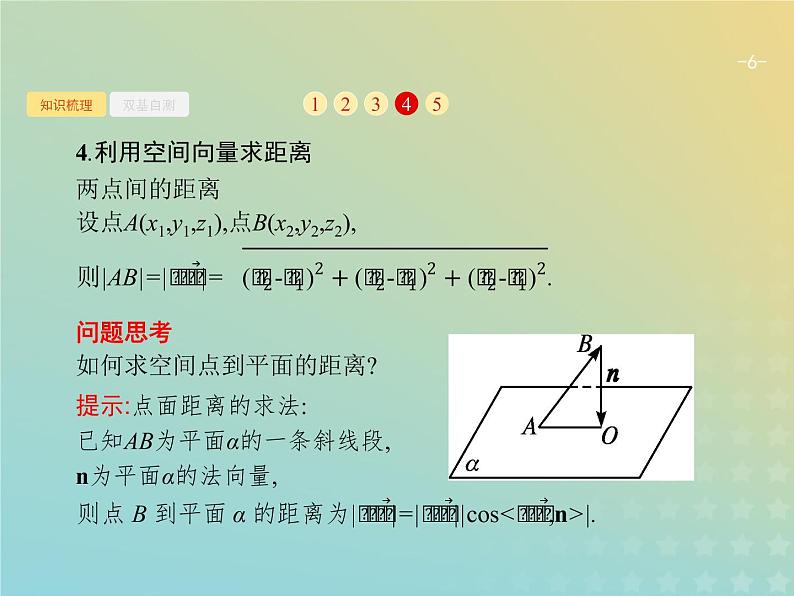
4.利用空间向量求距离两点间的距离设点A(x1,y1,z1),点B(x2,y2,z2),
问题思考如何求空间点到平面的距离?
提示:点面距离的求法:已知AB为平面α的一条斜线段,n为平面α的法向量,
1.下列结论正确的打“√”,错误的打“×”.(1)直线的方向向量是唯一确定的. (　　)(2)平面的单位法向量是唯一确定的. (　　)(3)若两条直线的方向向量不平行,则这两条直线不平行. (　　)(4)若空间向量a平行于平面α,则a所在直线与平面α平行. (　　)(5)两条直线的方向向量的夹角就是这两条直线所成的角. (　　)
2.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是(　　)
3.已知直三棱柱ABC-A1B1C1在空间直角坐标系中,如图所示,且CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为(　　)
4.在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为　　　　　. 
5.已知P是二面角α-AB-β棱上的一点,分别在平面α,β上引射线PM,PN,如果∠BPM=∠BPN=45°,∠MPN=60°,那么二面角α-AB-β的大小为　　　　　. 
例1如图所示,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点.求证:PB∥平面EFG.思考用向量法证明平行和垂直的常用方法有哪些?
证明:∵平面PAD⊥平面ABCD,且交线为AD,四边形ABCD为正方形,△PAD是直角三角形,∴AB,AP,AD两两垂直.以点A为坐标原点,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
解题心得1.用向量法证明平行类问题的常用方法
2.用向量法证明垂直类问题的常用方法
对点训练1如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.已知BC=8,PO=4,AO=3,OD=2.(1)求证:AP⊥BC;(2)若点M是线段AP上一点,且AM=3.试证明平面AMC⊥平面BMC.
证明 (1)如图所示,以点O为坐标原点,分别以射线OD,OP为y轴、z轴的正半轴建立空间直角坐标系Oxyz.∴O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0),P(0,0,4).
例2如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.(1)求证:B1E⊥AD1.(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.思考立体几何开放性问题的求解方法有哪些?
解题心得立体几何开放性问题的求解方法有以下两种:(1)根据题目的已知条件进行综合分析和观察猜想,找出点或线的位置,然后加以证明,得出结论;(2)假设所求的点或线存在,并设定参数表达已知条件,根据题目要求进行求解,若能求出参数的值且符合已知限定的范围,则存在这样的点或线,否则不存在.本题是设出点P的坐标,借助向量运算,判定关于z0的方程是否有解.
对点训练2如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.(1)求证:EF⊥CD;(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
解:如图,以D为原点,分别以DA,DC,DP所在直线为x轴、y轴、z轴建立空间直角坐标系.设AD=a,a>0,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),
考向一　利用空间向量求异面直线所成的角例3如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.思考如何利用向量法求异面直线所成的角?
从而EG2+FG2=EF2,所以EG⊥FG.因为四边形ABCD为菱形,所以AC⊥BD,又BE⊥平面ABCD,所以BE⊥AC.因为BD∩BE=B,所以AC⊥平面BDFE.因为EG⊂平面BDFE,所以AC⊥EG.又AC∩FG=G,可得EG⊥平面AFC.因为EG⊂平面AEC,所以平面AEC⊥平面AFC.
考向二　利用空间向量求直线与平面所成的角例4如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.思考如何利用向量法求线面角?
(1)证明：由已知可得,BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.(2)解：作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
建立如图所示的空间直角坐标系Hxyz.由(1)可得,DE⊥PE.
考向三　利用空间向量求二面角的大小例5图①是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②.(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的二面角B-CG-A的大小.思考如何利用向量法求二面角?
(1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,BC∩BE=B,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.
(2)解:作EH⊥BC,垂足为H.因为EH⊂平面BCGE,平面BCGE⊥平面ABC,且交线为BC,所以EH⊥平面ABC.由已知,菱形BCGE的边长为2,∠EBC=60°,
设平面ACGD的法向量为n=(x,y,z),
考向四　利用空间向量求点到平面的距离例6如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2 ,求点A到平面MBC的距离.思考如何利用向量法求点到平面的距离?
解:如图,取CD的中点O,连接OB,OM,则OB⊥CD,OM⊥CD.又平面MCD⊥平面BCD,交线为CD,所以MO⊥平面BCD.以O为坐标原点,直线OC,BO,OM分别为x轴、y轴、z轴,建立空间直角坐标系.因为△BCD与△MCD都是边长为2的正三角形,
设平面MBC的法向量为n=(x,y,z),
2.利用向量法求线面角的方法:(1)分别求出斜线和它在平面内的射影的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(或钝角的补角),取其余角就是斜线和平面所成的角.
3.利用向量法求二面角的方法:(1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的大小;(2)通过平面的法向量来求:设二面角的两个半平面的法向量分别为n1和n2,则二面角的大小等于(或π-).应注意结合图形判断二面角是锐角还是钝角.
4.利用向量法求点到平面的距离的方法:
对点训练3(1)如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1=2, ∠ACB=90°,D,E,F分别为AC,AA1,AB的中点.①求证:B1C1∥平面DEF;②求EF与AC1所成角的大小;③求点B1到平面DEF的距离.
(1)①证明:在直三棱柱ABC-A1B1C1中,B1C1∥BC.∵D,F分别是AC,AB的中点,∴FD∥BC,∴B1C1∥FD.又B1C1⊄平面DEF,DF⊂平面DEF,∴B1C1∥平面DEF.
②解:建立如图所示的空间直角坐标系,则C(0,0,0),A(2,0,0), B(0,2,0),A1(2,0,2),B1(0,2,2),C1(0,0,2),D(1,0,0),E(2,0,1),F(1,1,0).
③解:设向量n=(x,y,z)是平面DEF的法向量,
(2)如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ,∠BAD=120°.①求异面直线A1B与AC1所成角的余弦值;②求二面角B -A1D -A的正弦值.
(2)解:在平面ABCD内,过点A作AE⊥AD,交BC于点E.因为AA1⊥平面ABCD,所以AA1⊥AE,AA1⊥AD.
(3)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ,AB=4.①求证:M为PB的中点;②求二面角B-PD-A的大小;③求直线MC与平面BDP所成角的正弦值.
①证明:设AC,BD交点为E,连接ME.因为PD∥平面MAC,平面MAC∩平面PDB=ME,所以PD∥ME.因为ABCD是正方形,所以E为BD的中点.所以M为PB的中点.②解:取AD的中点O,连接OP,OE.因为PA=PD,所以OP⊥AD.又因为平面PAD⊥平面ABCD,交线为AD,且OP⊂平面PAD,所以OP⊥平面ABCD.因为OE⊂平面ABCD,所以OP⊥OE.因为ABCD是正方形,所以OE⊥AD.
如图,建立空间直角坐标系Oxyz,
(4)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, ∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.①证明:MN∥平面C1DE;②求二面角A-MA1-N的正弦值.
(4)①证明:连接B1C,ME.因为M,E分别为BB1,BC的中点,
因此四边形MNDE为平行四边形,MN∥ED.又MN⊄平面EDC1,所以MN∥平面C1DE.