2023年高考数学(文数)一轮复习课时54《变量间的相关关系统计案例》达标练习（2份，答案版+教师版）

这是一份2023年高考数学(文数)一轮复习课时54《变量间的相关关系统计案例》达标练习（2份，答案版+教师版），文件包含2023年高考数学文数一轮复习课时54《变量间的相关关系统计案例》达标练习含详解doc、2023年高考数学文数一轮复习课时54《变量间的相关关系统计案例》达标练习教师版doc等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
一、选择题
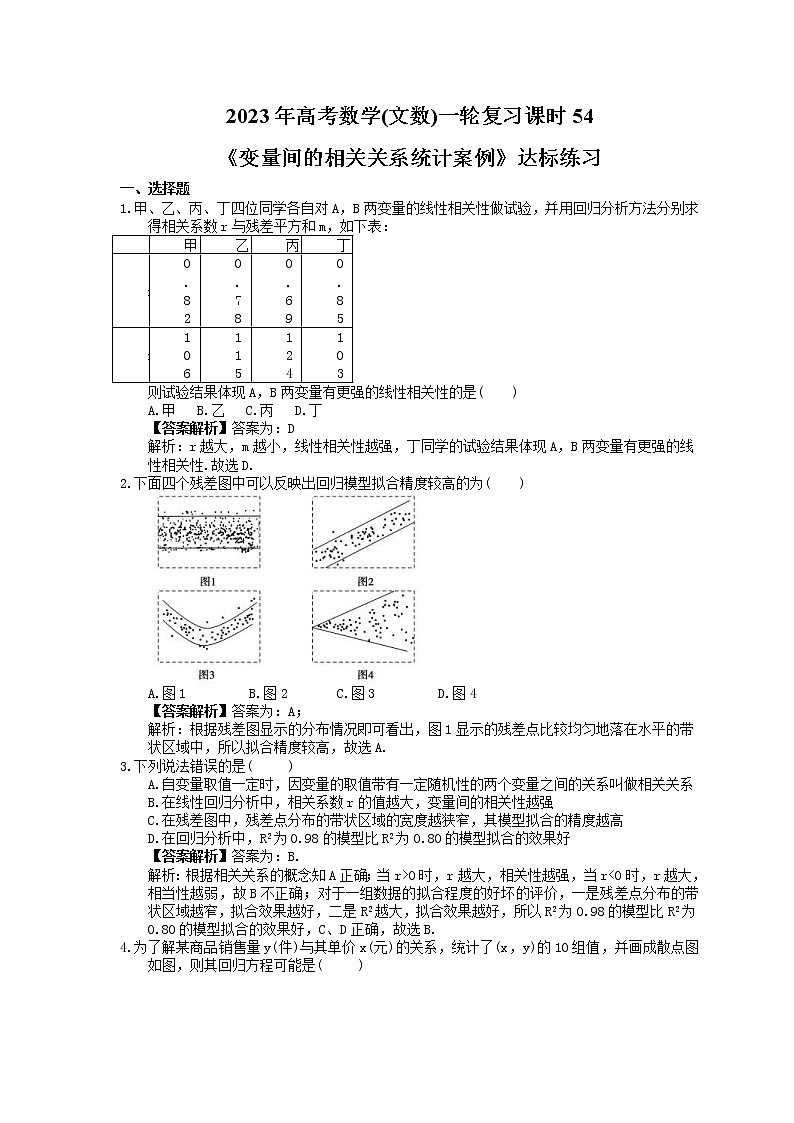
甲、乙、丙、丁四位同学各自对A，B两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r与残差平方和m，如下表：
则试验结果体现A，B两变量有更强的线性相关性的是( )
A.甲 B.乙 C.丙 D.丁
下面四个残差图中可以反映出回归模型拟合精度较高的为( )
A.图1 B.图2 C.图3 D.图4
下列说法错误的是( )
A.自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中，相关系数r的值越大，变量间的相关性越强
C.在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
D.在回归分析中，R2为0.98的模型比R2为0.80的模型拟合的效果好
为了解某商品销售量y(件)与其单价x(元)的关系，统计了(x，y)的10组值，并画成散点图如图，则其回归方程可能是( )
A.eq \(y,\s\up6(^))=－10x－198 B.eq \(y,\s\up6(^))=－10x＋198
C.eq \(y,\s\up6(^))=10x＋198 D.eq \(y,\s\up6(^))=10x－198
已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是( )
A.eq \(y,\s\up6(^))=1.23x＋4 B.eq \(y,\s\up6(^))=1.23x＋5 C.eq \(y,\s\up6(^))=1.23x＋0.08 D.eq \(y,\s\up6(^))=0.08x＋1.23
为考察A、B两种药物预防某疾病的效果，进行动物实验，分别得到如下等高条形图：

根据图中信息，在下列各项中，说法正确的是( )
A.药物A、B对该疾病均没有预防效果
B.药物A、B对该疾病均有显著的预防效果
C.药物A的预防效果优于药物B的预防效果
D.药物B的预防效果优于药物A的预防效果
已知变量x和y的统计数据如下表：
根据上表可得回归直线方程为x－0.25，据此可以预测当x=8时，=( )
A.6.4
已知某产品连续4个月的广告费用为xi(i=1,2,3,4)千元，销售额为yi(i=1,2,3,4)万元，
经过对这些数据的处理，得到如下数据信息：
①x1＋x2＋x3＋x4=18，y1＋y2＋y3＋y4=14；
②广告费用x和销售额y之间具有较强的线性相关关系；
③回归直线方程eq \(y,\s\up6(^))=eq \(b,\s\up6(^))x＋eq \(a,\s\up6(^))中的eq \(b,\s\up6(^))=0.8(用最小二乘法求得).
那么，当广告费用为6千元时，可预测销售额约为( )
A.3.5万元 B.4.7万元 C.4.9万元 D.6.5万元
下表提供了某厂节能降耗技术改造后在生产某产品的过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据，根据下表提供的数据，求出y关于x的线性回归方程为 SKIPIF 1 < 0 =0.7x＋0.35，则下列结论错误的是( )
A.回归直线一定过点(4.5,3.5)
B.产品的生产能耗与产量呈正相关
C.t的值为3.15
D.该产品每多生产1吨，则相应的生产能耗约增加0.7吨
已知变量x和y满足关系y=－0.1x＋1，变量y与z正相关.下列结论中正确的是( )
A.x与y正相关，x与z负相关
B.x与y正相关，x与z正相关
C.x与y负相关，x与z负相关
D.x与y负相关，x与z正相关
某公司一种型号的产品近期销售情况如下表：
根据上表可得到回归直线方程eq \(y,\s\up6(^))=0.75x＋eq \(a,\s\up6(^))，据此估计，该公司7月份这种型号产品的销售额约为( )
A.19.5万元 万元 万元 万元
某产品的广告费用x(万元)与销售额y(万元)的统计数据如下表：
根据上表可得回归方程eq \(y,\s\up15(^))=b^x＋eq \(a,\s\up15(^))中的b^=10.6，据此模型预测广告费用为10万元时销售额为( )
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
二、填空题
为了研究某种细菌在特定环境下随时间变化的繁殖规律，得如下实验数据，计算得回归直线方程为eq \(y,\s\up15(^))=0.85x－0.25.由以上信息，得到下表中c的值为________.
某单位为了了解用电量y(度)与气温x(℃)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：
由表中数据得回归直线方程y=bx＋a中的b=－2，预测当气温为－4 ℃时，
用电量约为____度.
某高校“统计初步”课程的教师随机调查了选该课程的一些学生的情况，具体数据如下表：
为了判断主修统计专业是否与性别有关系，根据表中的数据，得到
χ2=eq \f(50×13×20－10×72,23×27×20×30)≈4.844，因为χ2≥3.841，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为________.
针对时下的“韩剧热”，某校团委对“学生性别和喜欢韩剧是否有关”作了一次调查，其中女生人数是男生人数的eq \f(1,2)，男生喜欢韩剧的人数占男生人数的eq \f(1,6)，女生喜欢韩剧的人数占女生人数eq \f(2,3).若有95%的把握认为是否喜欢韩剧和性别有关，则男生至少有 人.
\s 0 答案解析
答案为：D
解析：r越大，m越小，线性相关性越强，丁同学的试验结果体现A，B两变量有更强的线性相关性.故选D.
答案为：A；
解析：根据残差图显示的分布情况即可看出，图1显示的残差点比较均匀地落在水平的带状区域中，所以拟合精度较高，故选A.
答案为：B.
解析：根据相关关系的概念知A正确；当r>0时，r越大，相关性越强，当r