

2021湖北省龙泉中学高三下学期5月月考数学试题含答案
展开龙泉中学2021届高三5月月考
数学试题
考试用时:120分钟 全卷满分:150分
★祝考试顺利★
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设复数的共轭复数为.若(为虚数单位),则的值为( )
A. B. C. 0 D.
【1题答案】
【答案】B
2. 2021年春季.新冠肺炎疫情在印度失控.下图是印度某地区在60天内感染新冠肺炎的累计病例人数y(万人)与时间t(天)的散点图.则下列最适宜作为此模型的回归方程的类型是( )
A. B. C. D.
【2题答案】
【答案】C
3. 五国际劳动节放假三天,甲、乙两名同学计划去敬老院做志愿者,若甲同学在三天中随机选一天,乙同学在前两天中随机选一天,且两名同学的选择互不影响,则他们在同一天去的概率为( )
A. B. C. D.
【3题答案】
【答案】B
4. 已知随机变量,且,则的最小值为( )
A. B. C. D.
【4题答案】
【答案】B
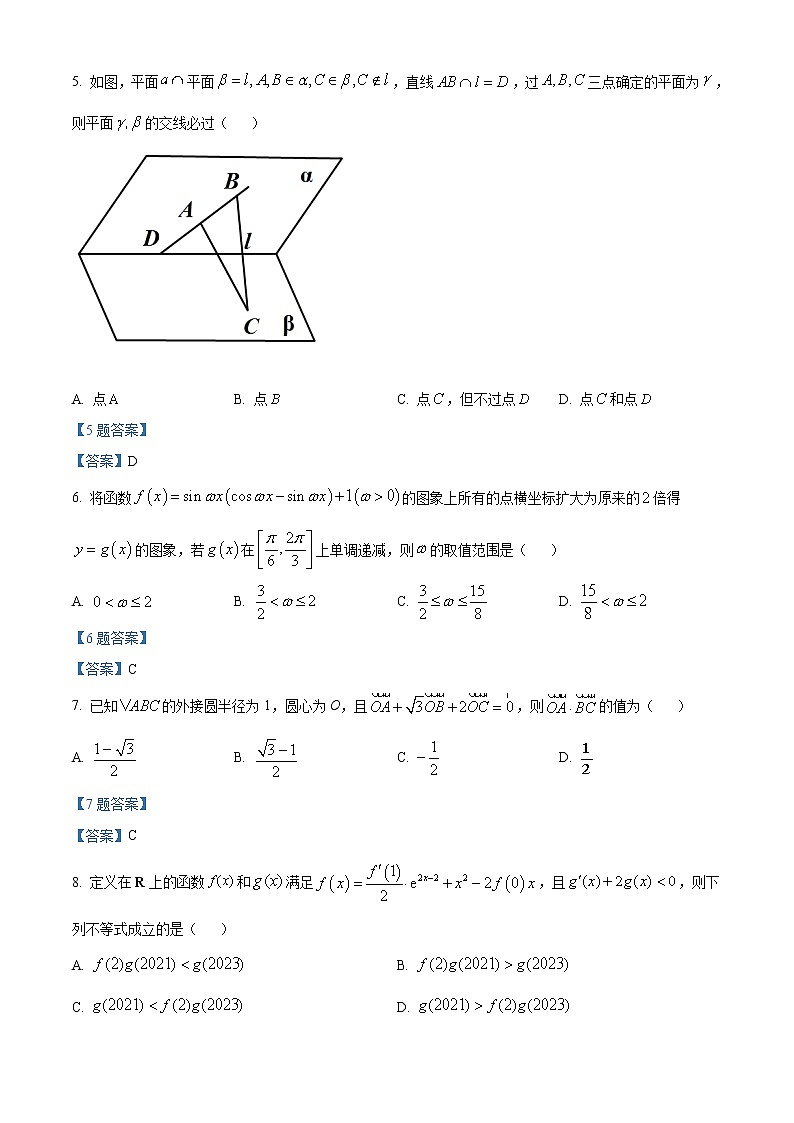
5. 如图,平面平面,直线,过三点确定的平面为,则平面的交线必过( )
A. 点 B. 点 C. 点,但不过点 D. 点和点
【5题答案】
【答案】D
6. 将函数的图象上所有的点横坐标扩大为原来的倍得的图象,若在上单调递减,则的取值范围是( )
A. B. C. D.
【6题答案】
【答案】C
7. 已知的外接圆半径为1,圆心为O,且,则的值为( )
A. B. C. D.
【7题答案】
【答案】C
8. 定义在R上的函数和满足,且,则下列不等式成立的是( )
A. B.
C. D.
【8题答案】
【答案】D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 是表示空气质量的指数,指数值越小,表明空气质量越好,当指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日指数值的统计数据,图中点A表示3月1日的指数值为201.则下列叙述正确的是( )
A. 这12天中有6天空气质量为“优良” B. 这12天中空气质量最好的是3月9日
C. 这12天的指数值的中位数是90.5 D. 从3月4日到9日,空气质量越来越好
【9题答案】
【答案】ABD
10. 在中,,则( )
A. B. 的面积为1
C. 外接圆直径是 D. 内切圆半径是
【10题答案】
【答案】ACD
11. 数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词源于希腊文,它的原意是“旋卷”或“缠卷”.小明对螺旋线有着浓厚的兴趣,连接嵌套的各个正方形的顶点就得到了近似于螺旋线的美丽图案,其具体作法是:在边长为1的正方形中,作它的内接正方形,且使得;再作正方形的内接正方形,且使得;与之类似,依次进行,就形成了阴影部分的图案,如图所示.设第个正方形的边长为(其中第1个正方形的边长为,第2个正方形的边长为,…),第个直角三角形(阴影部分)的面积为(其中第1个直角三角形的面积为,第2个直角三角形的面积为,…),则( )
A. 数列是公比为的等比数列 B.
C. 数列是公比为的等比数列 D. 数列的前项和
【11题答案】
【答案】BD
12. 已知椭圆的左、右焦点分别为是圆上且不在x轴上的一点,且的面积为.设C的离心率为e,,则( )
A. B. C. D.
【12题答案】
【答案】ACD
三、填空题:本题共4小题,每小题5分,共20分.
13. 若.且.则的展开式中的常数项为___________.
【13题答案】
【答案】
14. 《孙子算经》是我国南北朝时期(公元5世纪)的数学著作.在《孙子算经》中有“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即一个整数除以三余二,除以五余三,求这个整数.设这个正整数为a,当时,符合条件的所有a有_______个.
【14题答案】
【答案】53
15. 如图所示,一个圆锥的侧面展开图为以为圆心,半径长为2的半圆,点、在上,且的长度为,的长度为,则在该圆锥中,点到平面的距离为_________.
【15题答案】
【答案】
16. 双曲线的光学性质为①:如图,从双曲线右焦点发出的光线经双曲线镜面反射,反射光线的反向延长线经过左焦点.我国首先研制成功的“双曲线新闻灯”,就是利用了双曲线的这个光学性质.某“双曲线灯”的轴截面是双曲线一部分,如图②,其方程为,为其左右焦点,若从右焦点发出的光线经双曲线上的点A和点B反射后,满足,,则该双曲线的离心率为___________.
【16题答案】
【答案】
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知,它的内角的对边分别为,且,____.
①;②当时,函数取得最大值.在①②这两个条件中选择一个补充至上述横线上,求解下述问题:若问题中的三角形存在,能否求出边c的值?若能,请求出边c的值;若不能,请说明理由;若问题中的三角形不存在,请说明理由.
【17题答案】
【答案】答案不唯一,具体见解析.
18. 已知数列满足,且.
(1)求数列的通项公式;
(2)令,求数列的前项和.
【18题答案】
【答案】(1);(2).
19. 如图,四棱锥P-ABCD中,PA平面ABCD,,∠BAD=120o,AB=AD=2,点M在线段PD上,且DM=2MP,平面.
(1)求证:平面MAC平面PAD;
(2)若PA=6,求平面PAB和平面MAC所成锐二面角的余弦值.
【19题答案】
【答案】(1)证明见解析
(2)
21. 已知抛物线C∶y2=2px(p>0)的焦点为F,过点F且垂直于x轴的直线与C交于A,B两点,三角形AOB(点O为坐标原点)的面积为2.
(1)求抛物线C的方程;
(2)设不经过原点的直线与抛物线交于P,Q两点,设直线OP,OQ的倾斜角分别为α和β,证明:当时,直线恒过定点.
【21题答案】
【答案】(1);(2)证明见解析.
22. 羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现,需要领先对方2分才算该局获胜;③如果双方得分出现,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为;乙发球时,甲得分的概率为.
(Ⅰ)若,记“甲以赢一局”的概率为,试比较与的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为,的值.
| 甲得分 | 乙得分 | 总计 |
甲发球 |
| 50 | 100 |
乙发球 | 60 |
| 90 |
总计 |
|
| 190 |
①完成列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比赛中,双方战成,且轮到乙发球,记双方再战回合此局比赛结束,求的分布列与期望.
参考公式:,其中.
临界值表供参考:
0.15 | 0.10 | 0.05 | 0.010 | 0001 | |
2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
【22题答案】
【答案】(Ⅰ)(Ⅱ)①列联表见解析,有;②分布列见解析,
23. 已知函数.
(1)讨论函数的单调性;
(2)若,求证:.
【23题答案】
【答案】(1)答案见解析;(2)证明见解析.
湖北省荆门龙泉中学、宜昌一中2020-2021学年高三2月联考数学试题: 这是一份湖北省荆门龙泉中学、宜昌一中2020-2021学年高三2月联考数学试题,共4页。
湖北省荆门市龙泉中学2021届高三11月月考(期中)数学试题 Word版含答案: 这是一份湖北省荆门市龙泉中学2021届高三11月月考(期中)数学试题 Word版含答案,共4页。试卷主要包含了选择题的作答,非选择题的作答,考生必须保持答题卡的整洁,已知,则=,已知x,y∈,若f,设二次函数f,已知向量,则等内容,欢迎下载使用。
湖北省荆门市龙泉中学2023届高三5月模拟数学试题: 这是一份湖北省荆门市龙泉中学2023届高三5月模拟数学试题,共11页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。












