2021玉林高二下学期期末数学（理）试题含答案

玉林市2021年春季期高二年级期末教学质量监测

数学（理科）

本试卷分第Ⅰ卷（选择题共60分）和第Ⅱ卷（非选择题共90分），考试时间120分钟，满150分．考试结束后，只需上交答题卡．

注意事项：

1.答题前，考生务必在答题卡上用黑色签字笔将自己的姓名、准考证号填写清楚．请认真核对准考证号、姓名和科目．

2.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效．

第Ⅰ卷 选择题（共60分）

一、选择题（本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项填涂在答题卡上）

1.已知复数z满足z（1－i）＝5＋i，其中i为虚数单位，则z的虚部是（    ）

A.3        B.3i       C.2        D.2i

2.已知集合，则集合（    ）

A.        B.        C.或        D.

3.下列函数中，与函数的定义域与值域相同的是（    ）

A.        B.        C.        D.

4.已知a，b，c∈R，则“a＜b"”是“”的（    ）

A.充分非必要条件        B.必要非充分条件

C.充要条件              D.既非充分也非必要条件

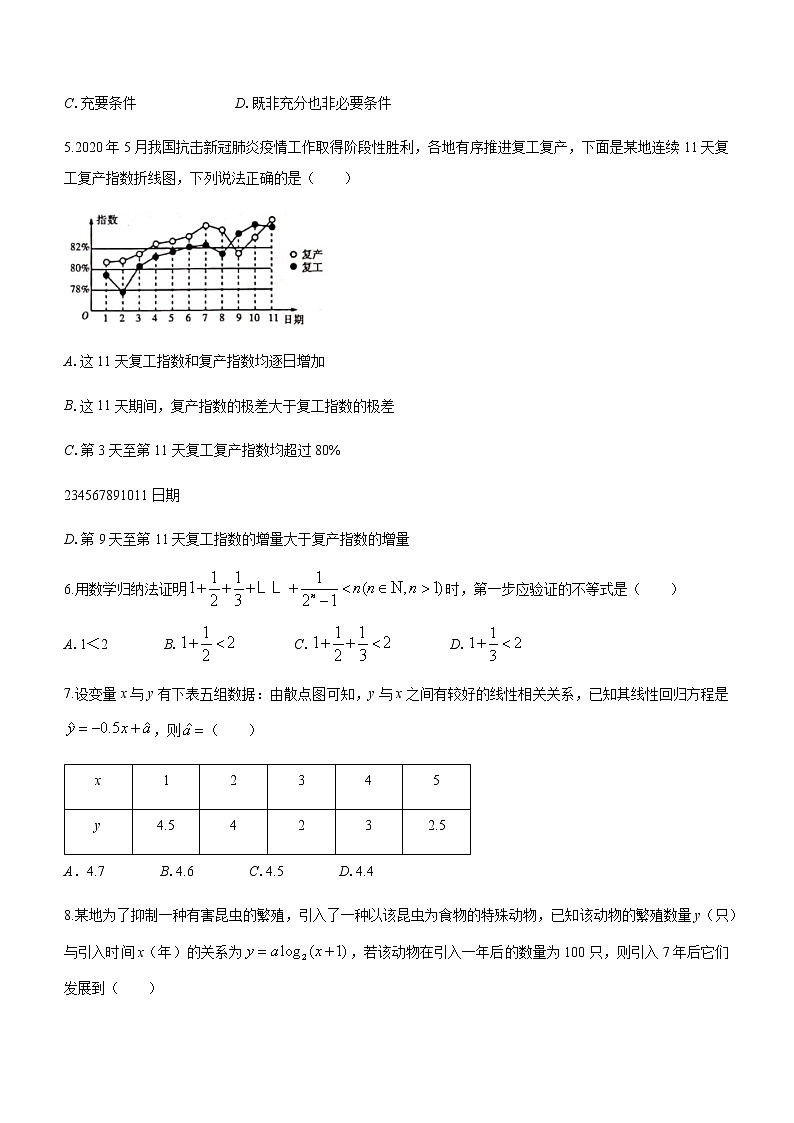
5.2020年5月我国抗击新冠肺炎疫情工作取得阶段性胜利，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（    ）

A.这11天复工指数和复产指数均逐日增加

B.这11天期间，复产指数的极差大于复工指数的极差

C.第3天至第11天复工复产指数均超过80%

234567891011日期

D.第9天至第11天复工指数的增量大于复产指数的增量

6.用数学归纳法证明时，第一步应验证的不等式是（    ）

A.1＜2        B.        C.        D.

7.设变量x与y有下表五组数据：由散点图可知，y与x之间有较好的线性相关关系，已知其线性回归方程是，则（    ）

A．4.7        B.4.6        C.4.5        D.4.4

8.某地为了抑制一种有害昆虫的繁殖，引入了一种以该昆虫为食物的特殊动物，已知该动物的繁殖数量y（只）与引入时间x（年）的关系为，若该动物在引入一年后的数量为100只，则引入7年后它们发展到（    ）

A.300只        B.400只        C.600只        D.700只

9.已知盒中装有大小形状完全相同的3个红球、2个白球、5个黑球．甲每次从中任取一球且不放回，则在他第一次な到的是红球的前提下，第二次拿到白球的概率为（    ）

A.       B.    C.     D.

10.曲线在点处的切线与该曲线及轴围成的封闭图形的面积为（    ）

11.设是定义在上的偶函数，且当时，．若对任意的，均有，则实数的最大值是（    ）

A.     B.   C.0    D.1

12.设，则（    ）

A.        B.        C.        D.

第Ⅱ卷  非选择题（共90分）

二、填空题（本题共4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上）

13.已知二项式，则其展开式中的常数项为        ．

14.已知函数为幂函数，且在为增函数，则        ．

15.地面上有并排的七个汽车位，现有红、白、黑三辆不同的汽车同时倒车入库，当停车完毕后，有且仅有两个空车位相邻的情况有        种．

16.在学习推理和证明的课堂上，老师给出两个曲线方程．老师问同学们：你想到了什么？能得到哪些结论？下面是四位同学的回答：

甲：曲线关于对称；

乙：曲线关于原点对称；

丙：曲线与坐标轴在第一象限围成的图形面积；

丁：曲线与坐标轴在第一象限围成的图形面积．

四位同学回答正确的有       （选填“甲、乙、丙、丁”）．

三、解答题（共70分．解答应写出文字说明、证明过程或演算步．第17~21题为必考题每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．）

（一）必考题：共60分．

17.（12分）设为实数，函数．

（1）求的极值；

（2）若恰好有两个零点，求的值．

18.（12分）某工厂生产一种汽车的元件，该元件是经过三道工序加工而成的，三道工序加工的元件合格率分别为．已知每道工序的加工都相互独立，三道工序加工都合格的元件为一等品；恰有两道工序加工合格的元件为二等品：其它的为废品，不进入市场．

（1）生产一个元件，求该元件为二等品的概率；

（2）若从该工厂生产的这种元件中任意取出3个元件进行检测，求恰有2个元件是一等品的概率．

19.（12分）已知函数

（1）解不等式；

（2）若关于x的方程在上有解，求m的取值范围．

20.（12分）某校为了解校园安全教育系列活动的成效，对全校学生进行一次安全意识测试，根据찌试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分．现随机抽取部分学生的成绩，统计结果及对应的频率分布直方图如下所示：

若测试的同学中，分数段内女生的人数分别为2人、8人、16人、4人，完成列联表，并判断：是否有90%以上的把握认为性别与安全意识有关？

（2）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中，共选取10人进行座谈，现再从这10人中任选4人，记所选4人的量化总分为，求的分布列及数学期望附表及公式

21.（12分）已知函数．

（1）若求的单调区间

（2）若恒成立，求整数a的最大值

（二）选考题：共10分．请考生在第22、23題中任选一题作答．如果多做，则按所做的第一题计分

22.（10分）

已知直线（为参数），曲线：：

（1）求直线的許通方程与曲线的直角坐标方程

（2）求直线被曲线所截得的弦长．

23.[选修4－5：不等式选讲]（10分）

已知函数．

（1）求不等式的解集；

（2）若为正实数，函数的最小值为t，且满足，求的最小值．

玉林市2021年春期高二年级期末教学质量监测

数学（理科）参考答案

一、选择题（共12小题）

1.A解：为，所以

所以z的虚部是3，故选：A．

2.D解： 故：D

3.B．解：由函数的定义域为，值域），

对于的定义域为，值域，错误；

对于的定义域为，值域，正确；

对于的定义域为，值域，错误

对于的定义域为，值域错误

故选：B．

4.B解：当时，；当时，说明

有得

显然左边不一定推导出右边，但右边可以推出左边，故送：B

5.C解：8天比第7天的复工指数和复产指数均低，A错

这11天期同，复产指数的极差小于复工指数的极差：两者最高差不多，但最低的复工指数比复产指数低得多，B错

第3天第11天复工复产指数均超过80%，C正确

第9天第11天复工指数的增量小于复产指数的增量，D错误

故选：C

6.C解：用数学归纳法证明时，第一步应验证不等式

为：．故选：C．

7.A解：，

线性回归方程是，所以．故选：A．

8.A解：将代入得，，

解得a＝100，所以x＝7时，．故选：A．

9.D解：设第1次拿到红球为事件A，第2次拿到白球为事件B，则，6，所以故选：D．

10.D解：，切点坐标为曲线在x＝1处的切线方程为曲线在点处的切线与该曲线及y轴围成的封闭图形的面积为．故选：D．

11.B解：当时，单调递减，且为偶函数，根据偶函数对称性可知，当x＞0时，f（x）单调递増，对任意的，均有，故，即，由区间的定义可知，b＞－1，

若x＋b≥0，则x＋b≥2x，即x≤b，由于x的最大值b＋1，故b≥x显然不恒成立，若，则即，解得，故b的最大值．故选：B

12.D解：设，，令，在（0，e）递增，在递减，，即，设，在[0，＋∞）上单调递増，，同理：，故选D．

二、填空题（共4小题）

13.160  解：二项式展开式的通项公式为，

令6－2r＝0，求得r＝3，故展开式中的常数项为，故答案为：160.

14.  解：因为函数为幂函数，且在x∈（0，＋∞）为增函数，

所以，解得．故答案为：．

15.72  解：根据题意，首先把三辆车排列有种排法，再把两个连续的空车位捆绑与另两个空车位往3辆车中插入有种方法，由乘法原理有种停法．

16.甲、乙、丙   解：甲说法：对曲线，交换x，y得，方程不变，所以关于y＝x对称，故甲说法正确；

乙说法：若（x，y）在曲线上，即，所以，即点（－x，－y）在曲线上，所以曲线关于原点对称，故乙说法正确；

丙说法：选择x＋y＝1作参考，其与坐标轴在第一象限围成的面积为，

对，第一象限均有，

此时，等号不能同时取得，所以，

所以时，x＋y＜1，且x＋y＝1时，，

所以曲线与坐标轴在第一象限围成的图形面积，故丙说法正确；

丁说法：选择作为参考，其与坐标轴在第一象限围成的面积为，

若，则，即，所以，

即曲线与坐标轴在第一象限围成的图形面积，故丁说法错误，

故答案为：甲、乙、丙．

三、解答题（共7小题）

17.解：（1）令得，…………2分

当x＜－1时，，当－1＜x＜1时，，当x＞1时，……………………4分

；………………6分

（2）当极大值或极小值为零时，y＝f（x）恰有两个零点，………………10分

则a＝2或a＝－2………………12分

18.解：（1）不妨设元件经A，B，C三道工序加工合格的事件分别为A，B，C

所以．…………2分

设事件D为“生产一个元件，该元件为二等品”．由已知A，B，C是相互独立事件．

根据事件的独立性、互斥事件的概率运算公式，

，

所以生产一个元件，该元件为二等品的概率为．…………6分

（2）生产一个元件，该元件为一等品的概率为．…………8分

设事件E为“任意取出3个元件进行检测，恰有2个元件是一等品”，

则．………………11分

所以恰有2个元件是一等品的概率为．

19.解：（1）因为………………3分

．所以不等式的解集为．………………6分

（2）令，因为，………………7分

所以关于x的方程f（x）＝m在[－1，1]上有解转化为在上有解………………8分

又因为在上为减函数，…………10分

所以，即．故m的取值范围．…………12分

20.解：（1）由频率分布直方图可知，得分在[20，40）的频率为0.005×20＝0.1，故抽取的学生答卷总数为．………………1分

性别与合格情况的2×2列联表为：

………………4分

即没有90%以上的把握认为性别与安全测试是否合格有关．………………5分

（2）“不合格”和“合格”的人数比例为24∶36＝2∶3，因此抽取的10人中“不合格”有4人，“合格”有6人，所以X可能的取值为20、15、10、5、0，……………………6分

，………………7分

，………………8分

，…………9分

．…………10分

X的分布列为：

………………11分

所以．………………12分

21.解：（1）f（x）的定义域为，

，………………1分

①当－1＜a＜0时，，由，得0＜x＜1或，由，得，

∴f（x）的单调减区间为，单调增区间为（0，1）和；…………2分

②当a＝－1时，在上恒成立，

∴f（x）的单调增区间为，无减区间；………………3分

③当a＜－1时，，由，得或x＞1，由，得，

∴f（x）的单调减区间为，单调增区间为和；………………4分

综上所述，当a＜－1时，f（x）的单调减区间为，单调増区间为和；

当a＝－1时，f（x）的单调增区间为，无减区间；

当－1＜a＜0时，f（x）的单调减区间为，单调增区间为（0，1）和．………………5分

（2），故，

设，则，………………6分

设，则恒成立，

∴h（x）在（0，＋∞）上单调递增，………………7分

∵h（1）＝－1＜0，，

，使得，…………8分

时，，从而，

时，在上为减函数，

时，，从而，

时，在上为増函数，………………9分

，把代入得：

，………………10分

令，则p（x）为增函数，

，，，

整数a的最大值为－1………………12分

22.解：（1）由，得………………1分

由，得．………………2分

即…………4分

；      ………………5分

（2）由，得．………………6分

曲线是以（1，1）为圆心，以1为半径的圆，圆心到直线3x－4y＝0的距离为．…………8分

∴直线被曲线所截的弦长为．……………………10分

23.解：（1）由不等式，可得，

则或或，………………3分

解得或或，………………4分

所以，

所以不等式的解集为．…………5分

（2）因为，

所以f（x）的最小值为t＝6，即2a＋2b＋c＝6，………………7分

由柯西不等式，得，…………9分

当且仅当，即时，等号成立，

所以的最小值是4．………………10分