


- 专题03 平行四边形-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版) 试卷 12 次下载
- 专题04 一次函数-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版) 试卷 13 次下载
- 期末复习模拟测试卷01-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版) 试卷 7 次下载
- 期末复习模拟测试卷02-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版) 试卷 9 次下载
- 期末复习模拟测试卷03-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版) 试卷 7 次下载
专题05 数据的分析-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版)
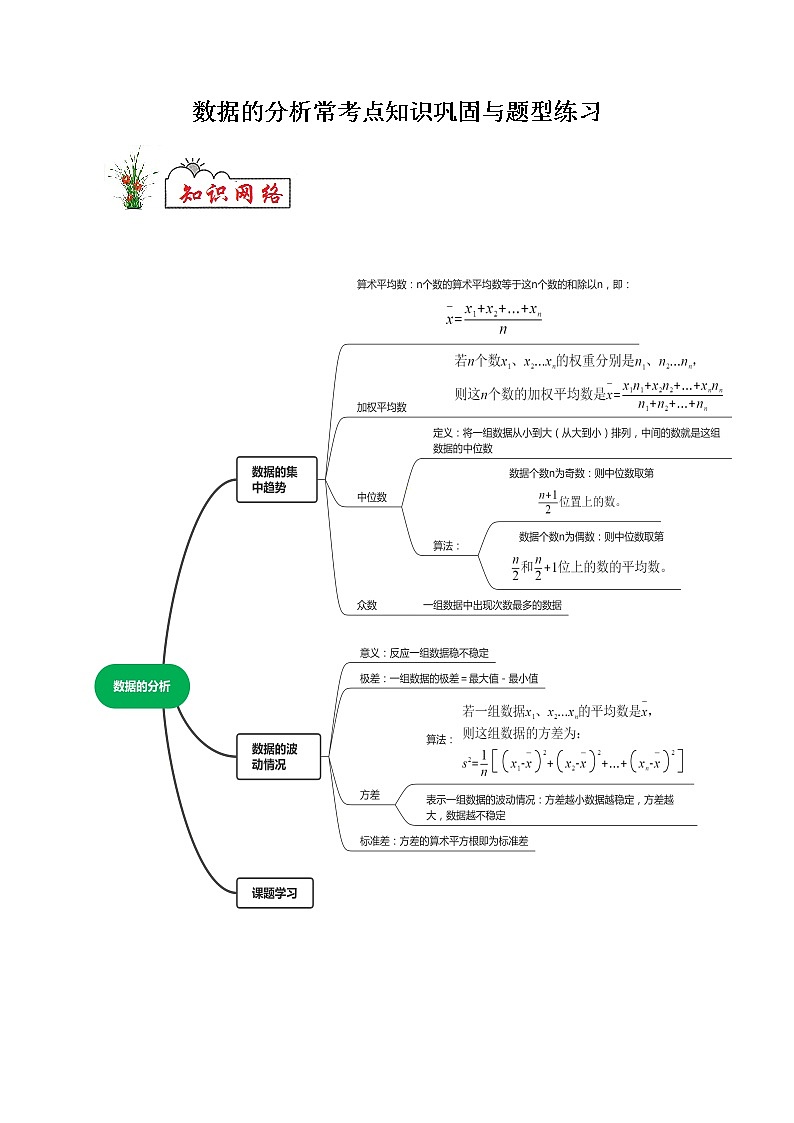
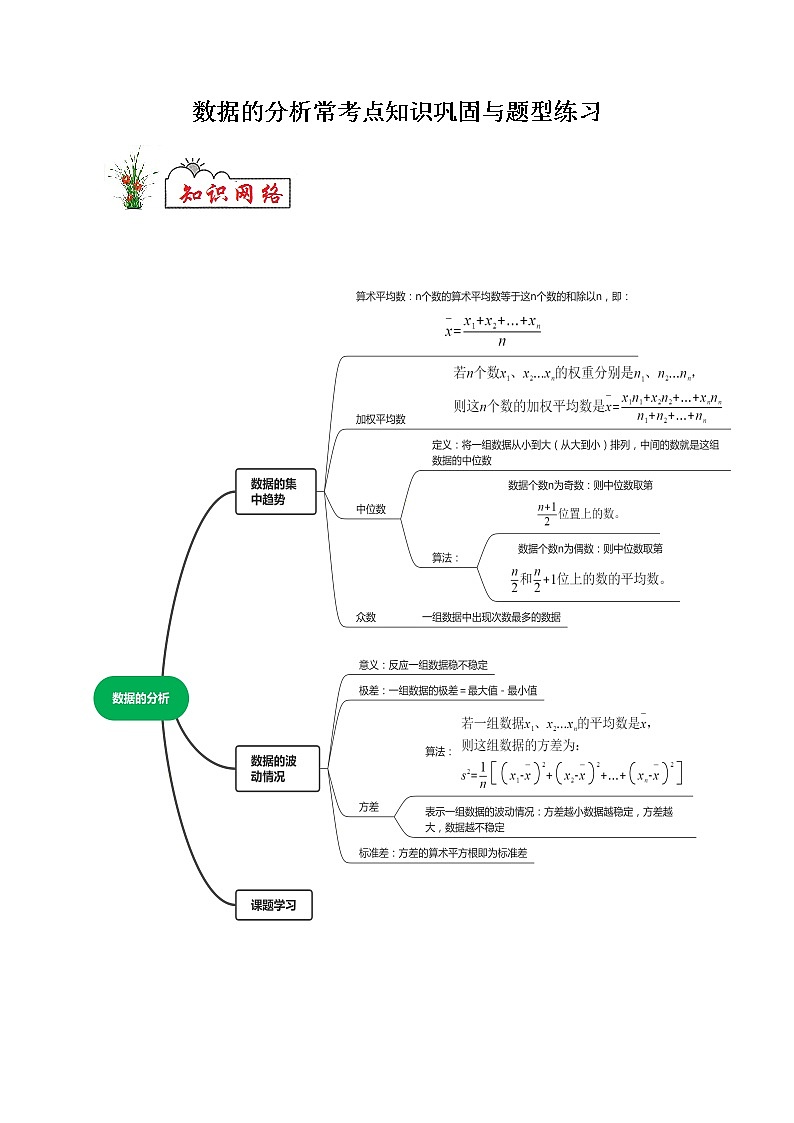
展开数据的分析常考点知识巩固与题型练习
考点一:数据的集中趋势
【知识点巩固】
算术平均数:
一组数据是,则这组数据的平均数为: 。
加权平均数:
若一组数据是,且他们的权重分别是,则这组数据的加权平均数为: 。
中位数:
定义:把一组数 排列, 位置上的数叫做这组数据的中位数。
算法:一组数据个数为n个,n为奇数时,则第 位上的数就是这组数据的中位数。n为偶数时,则第 和第 位上的两个数的平均数则为这组数据的中位数。
众数:
一组数据中出现次数 的那个数叫做这组数据的众数。
【例题:计算算术平均数】
1.小君周一至周五的支出分别是(单位:元):7,10,14,7,12.则这组数据的平均数是( )
A.7 B.10 C.11 D.11.5
2.若四个数据10,15,x,20的平均数是15,那么x的值为( )
A.10 B.20 C.15 D.25
3.在数据4,5,6,5中添加一个数据,而平均数不发生变化,则添加的数据为( )
A.0 B.5 C.4.5 D.5.5
4.如果x1与x2的平均数是5,那么x1﹣1与x2+5的平均数是( )
A.4 B.5 C.6 D.7
5.若a、b、c的平均数为7,则a+1、b+2、c+3的平均数为( )
A.7 B.8 C.9 D.10
【例题:加权平均数的计算】
6.2021年7月1日是中国共产党成立100周年纪念日,为了让全校学生树立爱国爱党的崇高信念,我市某学校开展了形式多样的党史学习教育活动.其中九年级举行了一场党史知识竞赛,在决赛中10名学生得分情况如表:
那么这10名学生所得分数的平均数是( )分.
分数 | 80 | 85 | 90 | 95 |
人数 | 1 | 3 | 4 | 2 |
A.88 B.88.5 C.90 D.无法确定
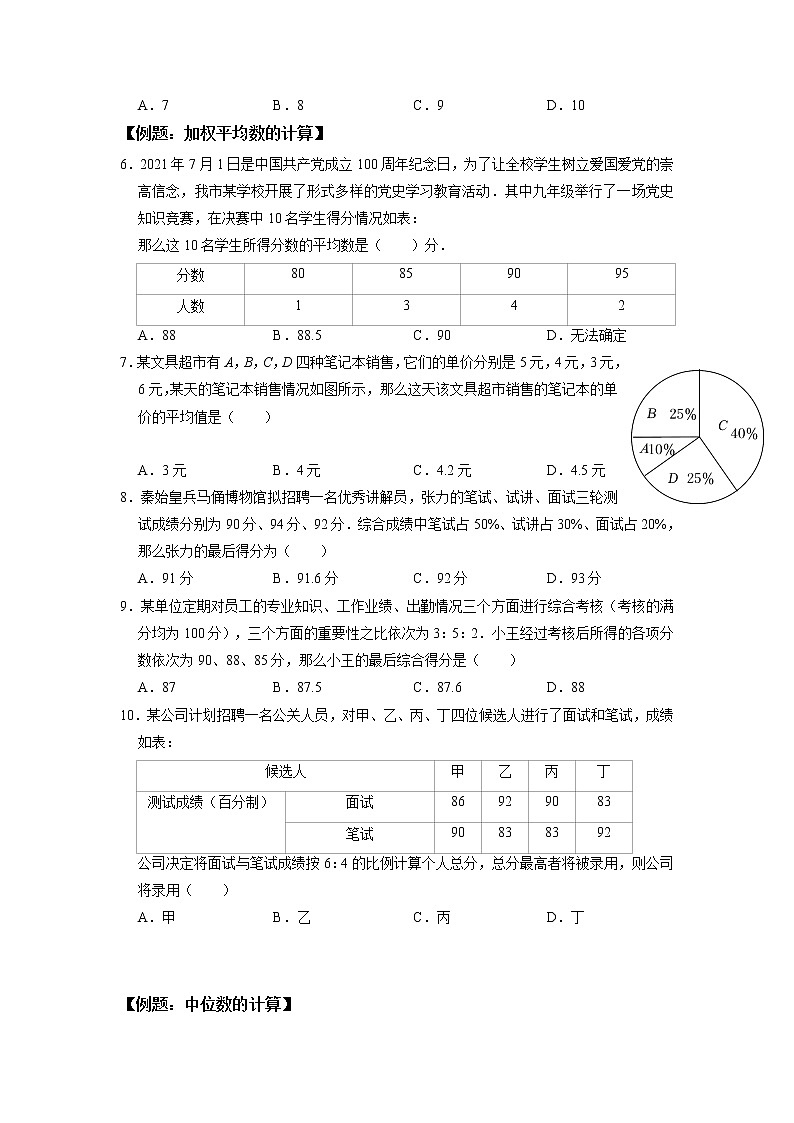
7.某文具超市有A,B,C,D四种笔记本销售,它们的单价分别是5元,4元,3元,6元,某天的笔记本销售情况如图所示,那么这天该文具超市销售的笔记本的单价的平均值是( )
A.3元 B.4元 C.4.2元 D.4.5元
8.秦始皇兵马俑博物馆拟招聘一名优秀讲解员,张力的笔试、试讲、面试三轮测试成绩分别为90分、94分、92分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么张力的最后得分为( )
A.91分 B.91.6分 C.92分 D.93分
9.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
10.某公司计划招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
公司决定将面试与笔试成绩按6:4的比例计算个人总分,总分最高者将被录用,则公司将录用( )
A.甲 B.乙 C.丙 D.丁
【例题:中位数的计算】
11.某班五个兴趣小组的人数分别为4,4,5,x,6.已知这组数据的平均数是5,则这组数据的中位数是( )
A.5 B.4 C.3 D.2
12.某女子羽毛球球队6名队员身高(单位cm)是170,174,178,180,180,184,因某种原因身高为174cm的队员退役,补上一位身高为178cm的队员后,该女子羽毛球队有关队员身高的数据正确的是( )
A.平均数变大,中位数不变
B.平均数变大,中位数变大
C.平均数变小,中位数不变
D.平均数变小,中位数变大
13.为庆祝中国共产党建党100周年,某机关单位进行党史知识竞赛,20名职工的成绩统计如下表,则这次党史知识竞赛成绩的中位数为( )
成绩/分 | 75 | 80 | 85 | 90 | 95 | 100 |
人数 | 1 | 2 | 5 | 6 | 5 | 1 |
A.80 B.85 C.90 D.87.5
14.为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如图统计图(每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A.中位数在60分~70分之间
B.中位数在70分~80分之间
C.中位数在80分~90分之间
D.中位数在90分~100分之间
15.一组数据:1,0,4,5,x,8.若它们的中位数是3,则x的值是( )
A.2 B.3 C.4 D.5
【例题:众数的计算】
16.在中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.67 | 1.68 | 1.69 | 1.73 | 1.75 | 1.80 |
人数 | 1 |
| 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.73,1.73 B.1.73,1.69 C.1.69,1.73 D.3,4
17.已知一组数据2,3,5,x,5,3有唯一的众数3,则x的值是( )
A.3 B.5 C.2 D.无法确定
18.“科学用眼,保护视力”是青少年珍爱生命的具体表现,某班50名同学的视力检查数据如下表:
视力 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
人数 | 2 | 3 | 6 | 9 | 12 | 10 | 5 | 3 |
则视力的众数是( )
A.4.5 B.4.6 C.4.7 D.4.8
考点二:数据的波动程度
【知识点巩固】
极差:
一组数据的极差等于这组数据的 减去 。
极差越大,数据波动 ,极差越小,数据波动 。
方差:
若一组数据的平均数为,这这组数据的方差为: 。
一组数据的方差越大,这组数据越 ,一组数据的方差越小,这组数据越 。
推广:若的平均数为,方差是。
则:的平均数为 ,方差为 。
的平均数为 ,方差为 。
的平均数为 ,方差为 。
标准差:方差的算术平方根是这组数据的标准差。
【例题:极差的计算】
19.若一组数据7,15,10,5,x,20的平均数是10,则这组数据的极差是( )
A.10 B.13 C.15 D.17
20.全国文明典范城市是全国文明城市的升级版,也是文明城市的标杆.2021年,长沙市抬高创建坐标,全力以赴推进“全国文明城市”向“全国文明典范城市”迭代升级.12月25日,长沙市文明办组织开展“长沙文明十二点”网络征集广纳建言活动,面向社会各界广泛征求意见和建议.芙蓉区某中学的小亮响应号召,对自己居住小区家庭使用垃圾袋的情况进行了调查,小亮随机调查了小区10户家庭一周垃圾袋的使用量,结果如下(单位:个):7,7,7,8,8,9,9,10,11,14,关于这组数据下列结论正确的是( )
A.平均数是10 B.众数是7 C.中位数是8 D.极差是6
21.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
22.如果一组数据﹣2,0,3,5,x的极差是9,那么x的值( )
A.9 B.7 C.﹣4 D.7或﹣4
【例题:方差的计算】
23.方差计算公式s2=[(4﹣7)2+(6﹣7)2+(8﹣7)2+(11﹣7)2+(6﹣7)2]中,数字5和7分别表示( )
A.数据个数、平均数 B.方差、偏差
C.众数、中位数 D.数据个数、中位数
24.一组样本数据为1、2、3、3、6,下列说法错误的是( )
A.平均数是3 B.中位数是3 C.方差是3 D.众数是3
25.一组数据1,2,a,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
26.如果数据x1,x2,…,xn的方差是3,则另一组数据2x1,2x2,…,2xn方差是( )
A.6 B.12 C.3 D.5
27.若x1,x2,x3,⋯,xn的平均数为8.方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
【例题:利用方差公式求其他统计量】
28.如果一组数据的方差是S=[(x1﹣20)2+(x2﹣20)2+…+(x12﹣20)2],已知9是这组数据中的一个数据,现把9去掉,则所得新数据的平均数是( )
A.12 B.15 C.18 D.21
29.小明在计算一组数据的方差时,列出的算式如下:s2=[2(7﹣)2+3(8﹣)2+(9﹣)2],根据算式信息,这组数据的众数是( )
A.3 B.6 C.7 D.8
30.在对一组样本数据进行分析时,小明列出了方差的计算公式:s2=[(8﹣)2+(6﹣)2+(9﹣)2+(6﹣)2+(11﹣)2],由公式提供的信息,判断下列关于样本的说法错误的是( )
A.平均数是8 B.众数是6 C.中位数是9 D.方差是3.6
【例题:方差的意义】
31.甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是S甲2=0.72,S乙2=0.75,S丙2=0.68,S丁2=0.61,则这四名同学立定跳远成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
32.通过统计甲、乙丙丁四名同学某学期的四次数学测试成绩,得到甲、乙、丙丁三名同学四次数学测试成绩的方差分别为S甲2=24,S乙2=18,S丙2=21,丁同学四次数学测试成绩(单位:分)如表:
| 第一次 | 第二次 | 第三次 | 第四次 |
丁同学 | 100 | 100 | 110 | 110 |
则这四名同学四次数学测试成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
33.2022年冬季奥运会将在北京市张家口举行,下表记录了四名短道速滑选手几次选拔赛成绩的平均数和方差s2:
| 小明 | 小红 | 小芳 | 小米 |
平均数(单位:秒) | 53 | m | 52 | 49 |
方差s2(单位:秒2) | 5.5 | n | 12.5 | 17.5 |
根据表中数据,可以判断小红是这四名选手中成绩最好且发挥最稳定的运动员,则m、n的值可以是( )
A.m=48,n=4 B.m=48,n=18 C.m=55,n=4 D.m=55,n=18
34.甲、乙两组数据的平均数相同,方差分别为m,n,甲组数据比乙组数据波动小,则m﹣n值为( )
A.正数 B.负数 C.0 D.非负数
人教版七年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测 期末复习模拟测试卷05(原卷版+解析): 这是一份人教版七年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测 期末复习模拟测试卷05(原卷版+解析),共24页。试卷主要包含了选择题,第四象限角平分线上,解答题等内容,欢迎下载使用。
期末复习模拟测试卷05-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版): 这是一份期末复习模拟测试卷05-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版),文件包含期末复习模拟测试卷05解析版docx、期末复习模拟测试卷05原卷版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
专题04 一次函数-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版): 这是一份专题04 一次函数-2021-2022学年八年级数学下学期期末复习常考点知识巩固+例题练习+期末模拟测试卷(人教版),文件包含专题04一次函数解析版docx、专题04一次函数原卷版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。












