数学基础模块上册(2021)4.2 弧度制完美版ppt课件

这是一份数学基础模块上册(2021)4.2 弧度制完美版ppt课件，共21页。PPT课件主要包含了情境导入，探索新知，例题辨析，巩固练习，归纳总结，布置作业，周长为2πcm，周长为4πcm，周长为10πcm等内容，欢迎下载使用。

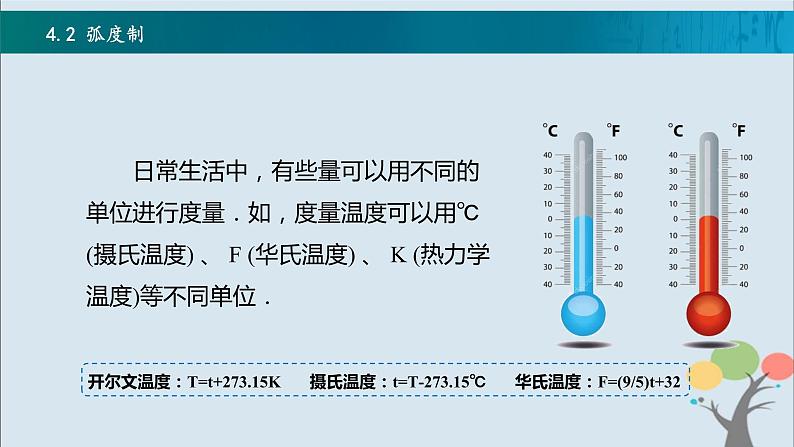
日常生活中，有些量可以用不同的单位进行度量．如，度量温度可以用℃ (摄氏温度) 、 F (华氏温度) 、 K (热力学温度)等不同单位．
在义务教育阶段, 用角度制来度量角．即把一个周角 360等分, 每一份圆弧所对的圆心角就是1°的角． 用角度制度量角用的是六十进制, 而日常的运算多数是十进制, 能否建立一种十进制的度量体系来度量角呢？
在半径分别为1cm、2cm、5cm的圆中, 圆周角所对的弧长与半径之比分别为多少？
可见，在不同半径的圆中, 同一度数角的弧长与其半径之比是相等的.
同时规定，正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是零.
其中,角α的正负由角α的终边的旋转方向决定.
用弧度制表示角时,可以省略单位“rad”．如“2rad”可以写成“2”． 但是,在用角度制表示角时,不能省略单位“°”.
例1 把−100°转换为弧度.
例4 利用科学型计算器进行角度与弧度的转换：(1)把67°30′转换为弧度(保留到小数点后第2位)；(2)把3.14rad转换为角度(保留到小数点后第2位)．
分析 利用科学型计算器进行角度与弧度的转换时，应先确定角的度量单位．设置角的度量单位为“度”或“弧度”的方法是：依次按键：SHIFT→MODE SETUP→3(角度制模式)或4(弧度制模式).
解 (1)第一步：将科学型计算器设为弧度制模式：
第二步：输入67°30′，并把它转换为弧度：
因此， 67°30′≈1.18rad．
结果显示1.178097245．
解 (2)第一步：将科学型计算器设为角度制模式：
第二步：输入3.14rad，并把它转换为角度：
结果显示179.9087477．
因此， 3.14 rad≈179.91°．
一些特殊角的角度值和弧度值的对应关系：
1．把下列角度转换为弧度． (1)22°； (2) −210°； (3) 1200°．
2．把下弧度转换为角度．
3．经过4h，时钟的时针和分针各转了多少度，转换为弧度是多少？
4．用弧度制表示终边在x轴上的角的集合.
5．已知一个扇形的半径为10 cm，圆心角为1.2rad，求该扇形的弧长和面积．
1.书面作业：完成课后习题和学习与训练；2.查漏补缺：根据个人情况对课题学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.