2022年河南省许昌市第二次中招模拟考试试卷数学（二模 ） (word版无答案)

XCS2022年第二次中招模拟考试试卷

九年级数学

注意事项：

1.本试卷共6页，三个大题，满分120分，考试时间100分钟.

2.本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上.答在试卷上的答案无效.

一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的.

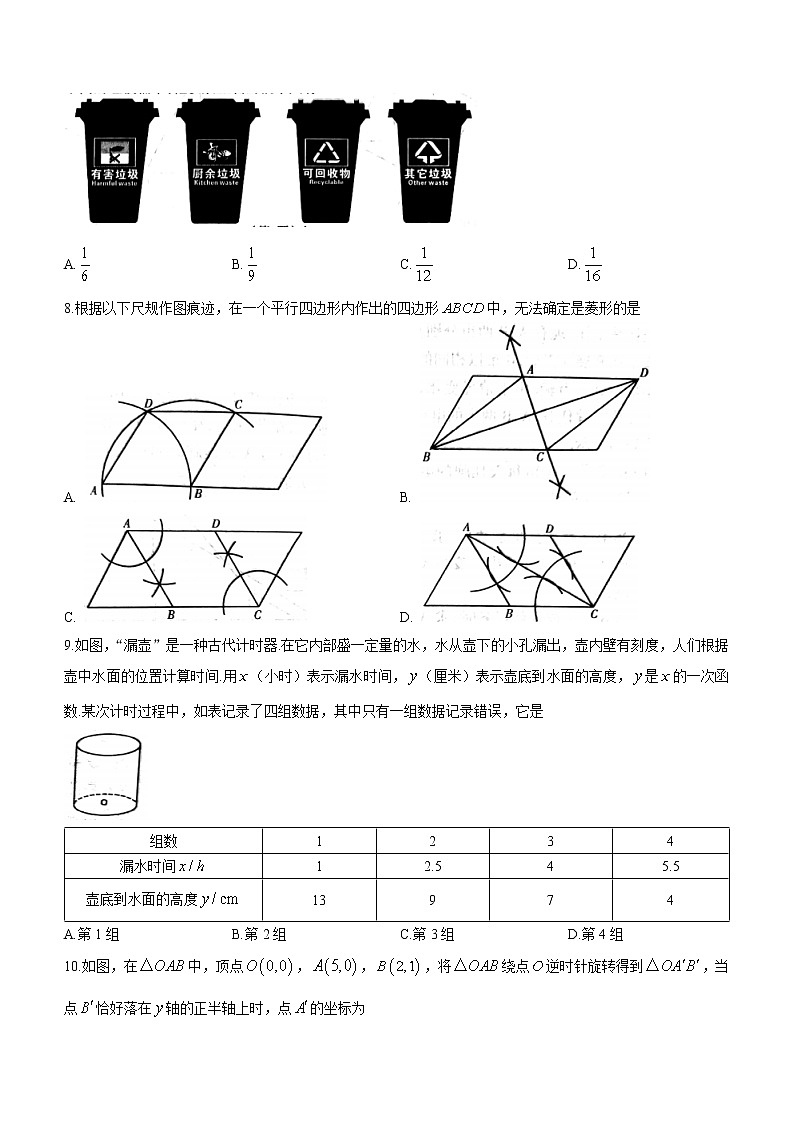
1.下列各数中，最小的数是

A.6 B. C.0 D.

2.在物联网时代的所有芯片中，14nm芯片已成为需求的焦点.已知nm即纳米，是长度的度量单位，.将14nm用科学记数法表示为

A. B. C. D.

3.把如图中的纸片沿虚线折叠，可以围成一个几何体，这个几何体的名称是

A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱

4.如图，已知直线，，，那么的度数是

A.55° B.65° C.75° D.115°

5.下列计算中，正确的是

A. B. C. D.

6.函数中自变量的取值范围是

A. B. C.且 D.且

7.垃圾分类可以把有用的垃圾回收再利用，减少了对环境的危害.王老师教上幼儿园的儿子学习垃圾分类，将一个饮料瓶和一个用过的电池交给儿子，调皮的儿子将两件垃圾随意投放到两个不同的垃圾桶中，他投放正确的概率只有

A. B. C. D.

8.根据以下尺规作图痕迹，在一个平行四边形内作出的四边形中，无法确定是菱形的是

A.  B.  

C.  D.

9.如图，“漏壶”是一种古代计时器.在它内部盛一定量的水，水从壶下的小孔漏出，壶内壁有刻度，人们根据壶中水面的位置计算时间.用（小时）表示漏水时间，（厘米）表示壶底到水面的高度，是的一次函数.某次计时过程中，如表记录了四组数据，其中只有一组数据记录错误，它是

A.第1组 B.第2组 C.第3组 D.第4组

10.如图，在中，顶点，，，将绕点逆时针旋转得到，当点恰好落在轴的正半轴上时，点的坐标为

A. B. C. D.

二、填空题（每小题3分，共15分）

11.____________.

12.分式方程的解是_____________.

13.如图是甲、乙两人6次投篮测试（每次投篮10个）成绩的统计图，甲、乙两人测试成绩的方差分别记作、，则_____________.（填“＞”，“＝”或“＜”）

14.如图1，是一枚残缺的古代钱币.图2是其几何示意图，正方形的边长是1cm，的直径为2cm，且正方形的中心和圆心重合，，分别是，的延长线与的交点，则钱币残缺部分（即图2中阴影部分）的面积是___________.

15.如图，为等腰直角三角形，，，点为边上一点，且，点为边上一动点（点不与点、重合），连接，将沿翻折得到，当的一边过点时，的长为___________.

三、解答题（本大题共8个小题，满分75分）

16.（10分）（1）计算：.

（2）解不等式组：.

17.（9分）某市各中小学为落实教育部政策，全面开展课后延时服务.市教育局为了解该市中学延时服务情况，随机抽查甲、乙两所中学各100名家长进行问卷调查.家长对延时服务的综合评分记为，将所得数据分为5组（“很满意”：；“满意”：；“比较满意”：；“不太满意”：；“不满意”：），市教育局对数据进行了分析.部分信息如下：

c.甲、乙两所中学延时服务得分的平均数、中位数、众数如表：

d.甲中学“满意组”的分数从高到低排列，排在最后的10个数分别是：

83，83，83，83，82，81，81，81，80，80.

请你根据以上信息，回答下列问题：

（1）直接写出和的值；

（2）根据以上数据，你认为哪所中学的延时服务开展得更好？并说明理由（一条即可）；

（3）市教育局指出：延时服务综合得分在70分及以上才算合格，请你估计乙中学1000名家长中认为该校延时服务合格的人数.

18.（9分）如图，在平面直角坐标系中，反比例函数的图象和矩形都在第一象限，平行于轴，且，，点的坐标为.

（1）直接写出，，三点的坐标；

（2）若将矩形向下平移，矩形的两个顶点、恰好同时落在反比例函数的图象上，请求出矩形的平移距离和的值.

19.（9分）闻听三国事，每欲到许昌.在许昌老城区的魏武帝广场中心，矗立着曹操雕像，这尊雕像是由中央美院设计创作，取意于毛主席诗词《浪淘沙·北戴河》中“往事越千年，魏武挥鞭，东临碣石有遗篇”的意境.某校数学兴趣小组在学习了“解直角三角形”之后，开展了测量这尊雕像（）高度的实践活动，三个兴趣小组设计了不同方案，测量数据如表：

（1）根据测量方案和测量数据，你认为第__________小组的数据无法算出雕像（）高度；

（2）请根据测量报告，选择其中一个可行方案及其测量数据，求出雕像（）的高度.

（结果保留整数，参考数据：，，）

20.（9分）为改善交通秩序，保障群众安全，自2021年起，河南省各地市陆续开展电动车登记挂牌工作.现有A、B两市分别对本市各30万辆电动车进行登记挂牌，在A市登记挂牌工作开展5天后，B市以相同的速度进行电动车登记挂牌工作，B市经过10天后挂牌车辆达到万辆.由于情况变化，B市挂牌速度加快，结果30天完成挂牌任务，A市50天完成挂牌任务.A、B两市的电动车挂牌车辆（万辆）与A市挂牌时间（天）之间的关系如图所示.

（1）直接写出A市每天挂牌的电动车车辆数及的值；

（2）当B市挂牌速度加快后，求关于的函数解析式，并写出自变量的取值范围；

（3）当B市完成挂牌任务时，求A市未挂牌的电动车辆数.

21.（9分）《几何原本》是古希腊数学家欧几里得所著的一部数学著作，书中以23个定义、5个公设和5个公理作为基本出发点，给出了119个定义和465个命题.其中，命题4.2的内容是：给定一个三角形，可作圆内接相似三角形.

小冉想尝试对这个命题进行证明，于是根据书中命题的内容及图形的画法写出了已知和求证：

已知：如图1，为已知三角形，如图2，是的切线，为切点，，.

求证：.

小冉在图2的基础上，添加了辅助线；如图3，连接并延长，交于点，连接，.

（1）请在小冉所添辅助线的基础上，求证：；

（2）若，，，求的半径.

22.（10分）对于二次函数，在函数值的情况下，只有一个自变量的值与其对应.

（1）求二次函数的解析式；

（2）若在自变量的值满足的情况下，与其对应的函数值的最小值为3，求的值.

23.（10分）【问题情境】数学课上，王老师出示了这样一个问题：如图1，在矩形中，，是延长线上一点，且，连接，交于点，以为一边在的左下方作正方形，连接.试判断线段与的位置关系.

【探究展示】小明发现，垂直平分，并展示了如下的证明方法：

证明：∵，∴.

∵，∴.

∵四边形是矩形，∴.

∴_______________.（平行线分线段成比例）

∵，∴.∴.

即是的边上的中线，

又∵，∴_______________.（等腰三角形的“三线合一”）

∴垂直平分.

【反思交流】

（1）请将上述证明过程补充完整；

（2）小颖受到小明的启发，继续进行探究，如图2，连接，以为一边在的左下方作正方形，发现点在线段的垂直平分线上，请你给出证明；

【拓展应用】

（3）如图3，连接，以为一边在的右上方作正方形，分别以点，为圆心，为半径作弧，两弧交于点，连接.若，请直接写出的值.