新人教A版高考数学二轮复习专题十一概率与统计5变量间的相关关系统计案例综合篇课件

这是一份新人教A版高考数学二轮复习专题十一概率与统计5变量间的相关关系统计案例综合篇课件，共25页。

(2)回归直线方程(i)最小二乘法:通过求Q= (yi-bxi-a)2的最小值而得到回归直线的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做③　最小二乘法    .(ii)回归方程:方程 = x+ 是两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(xn,yn)的回归方程,其中 , 是待定参数. (3)相关系数r
 (ii)当r>0时,表明两个变量④　正相关    ;当r<0时,表明两个变量⑤　负相关    .r的绝对值越接近于1,表明两个变量的线性相关性越强;r的绝对值越接近 于0,表明两个变量之间几乎不存在线性相关关系.当r的绝对值大于或等 于0.75时,认为两个变量有很强的线性相关关系.(4)回归分析是对具有相关关系的两个变量进行统计分析的一种常用方 法.在线性回归模型y=bx+a+e中,因变量y的值由自变量x和随机误差e共同 确定,即自变量x只能解释部分y的变化,在统计中,我们把自变量x称为解
释变量,因变量y称为预报变量.
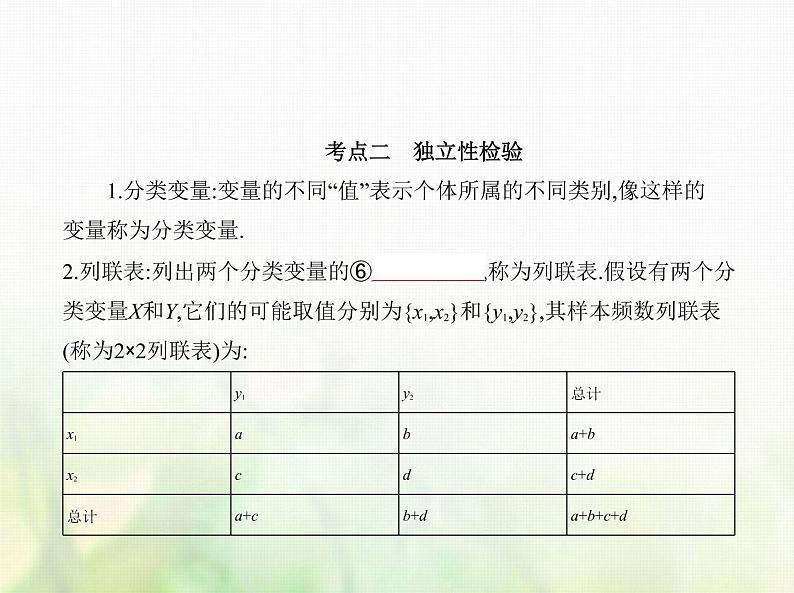
考点二　独立性检验　　1.分类变量:变量的不同“值”表示个体所属的不同类别,像这样的 变量称为分类变量.2.列联表:列出两个分类变量的⑥　频数表    ,称为列联表.假设有两个分 类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表 (称为2×2列联表)为:
　　可构造一个随机变量K2= ,其中n=a+b+c+d为样本容量.3.独立性检验利用独立性假设、随机变量⑦    K2    来确定是否有一定把握认为“两个 分类变量有关系”的方法称为两个分类变量的独立性检验.两个分类变量X和Y是否有关系的判断标准:统计学研究表明:当K2≤3.841时,认为X与Y无关;当K2>3.841时,有95%的把握说X与Y有关;当K2>6.635时,有99%的把握说X与Y有关;当K2>10.828时,有99.9%的把握说X与Y有关.
考法一　线性回归分析的应用
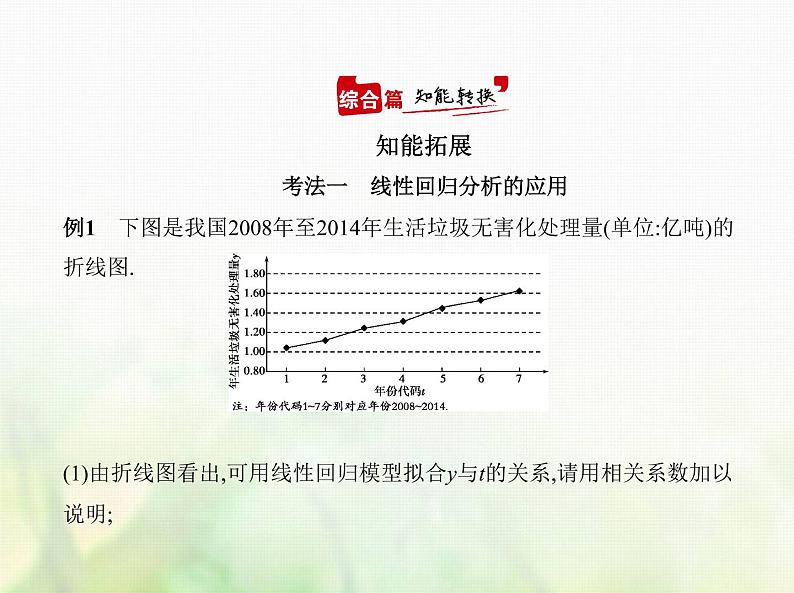
例1　下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的 折线图.(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
将2016年对应的t=9代入回归方程得 =0.93+0.10×9=1.83.所以预测2016年我国生活垃圾无害化处理量约为1.83亿吨.(12分)
例    (2019广东深圳第二次调研,18)某网店经销某商品,为了解该商品的 月销量y(单位:千件)与当月售价x(单位:元/件)之间的关系,收集了5组数据 进行了初步处理,得到下表:
　　(1)统计学中用相关系数r来衡量两个变量之间线性相关关系的强弱, 若|r|∈[0.75,1],则认为相关性很强;若|r|∈(0.25,0.75),则认为相关性一般; 若|r|∈[0,0.25],则认为相关性较弱.请计算相关系数r,并说明y与x之间的线 性相关关系的强弱(精确到0.01);
(3)由题意可知,月销售额的预估值 =1 000· ·x=-1 250x2+13 750x(元)或者 = ·x=-1.25x2+13.75x(千元). (10分)则当x=5.5时, 取到最大值,即该店主将售价定为5.5元/件时,可使网店的月销售额最大.(12分)
考法二　独立性检验的应用
例2    (2019湘东六校联考,19)市教育部门为研究高中学生的身体素质与 课外体育锻炼时间的关系,对该市某校200名高中学生平均每天的课外体 育锻炼时间进行了调查,数据如下表:
　　将学生日均课外体育锻炼时间在[40,60]内的学生评价为“课外体育 达标”.(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断 是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性 别有关;
　　(2)从上述课外体育不达标的学生中,按性别用分层抽样的方法抽取10名学生,再从这10名学生中随机抽取3人了解他们锻炼时间偏少的原因, 记所抽取的3人中男生的人数为随机变量X,求X的分布列和数学期望;(3)将上述调查所得到的频率视为概率来估计全市的情况,现在从该市所 有高中学生中抽取4名学生,求其中恰好有2名学生课外体育达标的概率.参考公式:K2= ,其中n=a+b+c+d.
K2= ≈6.061<6.635,所以在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与 性别有关. (4分)(2)易知,所抽取的10名学生中,男生有10× =4名,女生有10× =6名.X可取0,1,2,3.P(X=0)= = ,P(X=1)= = ,P(X=2)= = ,P(X=3)= = .∴X的分布列为
E(X)=0× +1× +2× +3× = . (9分)(3)设所抽取的4名学生中,课外体育达标的人数为ξ,由(1)中表格可知学生 课外体育达标的频率为 = ,将频率视为概率,∴ξ~B ,∴P(ξ=2)= × × = .∴恰好有2名学生课外体育达标的概率为 . (12分)
方法总结　独立性检验的一般步骤:(1)独立性检验原理只能解决两个对象,每个对象有两类属性的问题,所以 对于一个实际问题,我们要首先确定能否用独立性检验的思想加以解决;(2)如果确实属于这类问题,要科学地抽取样本,样本容量要适当,不可太 小;(3)根据数据列出2×2列联表;(4)提出假设H0:所研究的两类对象(X,Y)无关;(5)根据公式计算K2= (n=a+b+c+d)的值;(6)比较观测值k与临界值表中相应的检验水平,根据小概率原理肯定或者 否定假设,即判断X、Y是否相关.
例    (2018河南开封一模,19)近年来我国电子商务行业迎来蓬勃发展的新 机遇,2017年双十一期间,某购物平台的销售业绩高达1 271亿元人民币. 与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从 评价系统中选出200次成功交易,并对其评价进行了统计,其中对商品的 好评率为0.6,对服务的好评率为0.75,对商品和服务都作出好评的交易为 80次.(1)完成下面的2×2列联表,并回答是否有99%的把握认为商品好评与服务 好评有关;
　　(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对 商品和服务全好评的次数为随机变量X.①求对商品和服务全好评的次数X的分布列;②求X的数学期望和方差.附:
　    K2= ,其中n=a+b+c+d.
解析　(1)由题意可得关于商品和服务评价的2×2列联表如下:
　    K2= ≈11.111>6.635,故有99%的把握认为商品好评与服务好评有关.(2)①每次购物时,对商品和服务全好评的概率为 ,且X的取值可以是0,1,2,3.其中P(X=0)= = ,P(X=1)= × × = ,P(X=2)= × × = ,P(X=3)= × = ,