2022届贵州省贵阳市五校（贵阳民中 贵阳九中 贵州省实验中学 贵阳二中 贵阳八中）高三下学期联考（五）数学（文）试题含解析

2022届贵州省贵阳市五校（贵阳民中 贵阳九中 贵州省实验中学 贵阳二中 贵阳八中）高三下学期联考（五）

数学（文）试题

一、单选题

1．设集合，，则（       ）

A． B． C． D．

【答案】B

【分析】化简集合即得解.

【详解】解：由题得，

所以.

故选：B

2．设复数，则的的虚部是（       ）

A． B． C． D．

【答案】A

【分析】利用复数乘方运算和除法运算化简复数，再根据复数的概念可得结果.

【详解】,

所以的的虚部是.

故选：A

3．随着消费者环保意识的增强，新能源汽车得到了消费者的青睐.如图是某品牌的新能源汽车在今年的前8个月的销量（单位：辆）情况，以下描述错误的是（       ）

A．这8个月销量的极差是3258 B．这8个月销量的中位数是3194

C．这8个月中2月份的销量最低 D．这8个月中销量比前一个月增长最多的是4月份

【答案】B

【分析】根据折线图提供的数据结合极差、中位数等概念判断．

【详解】极差是，A正确；

中位数是，B错误；

这8个月中2月份的销量最低，C正确；

这8个月中销量比前一个月增长最多的是4月份，增加1619．D正确．

故选：B．

4．若，则（       ）

A． B． C． D．

【答案】A

【分析】应用诱导公式、倍角正余弦公式及同角三角函数的关系化成齐次式形式，进而可得，结合已知求值即可.

【详解】，

故选：A.

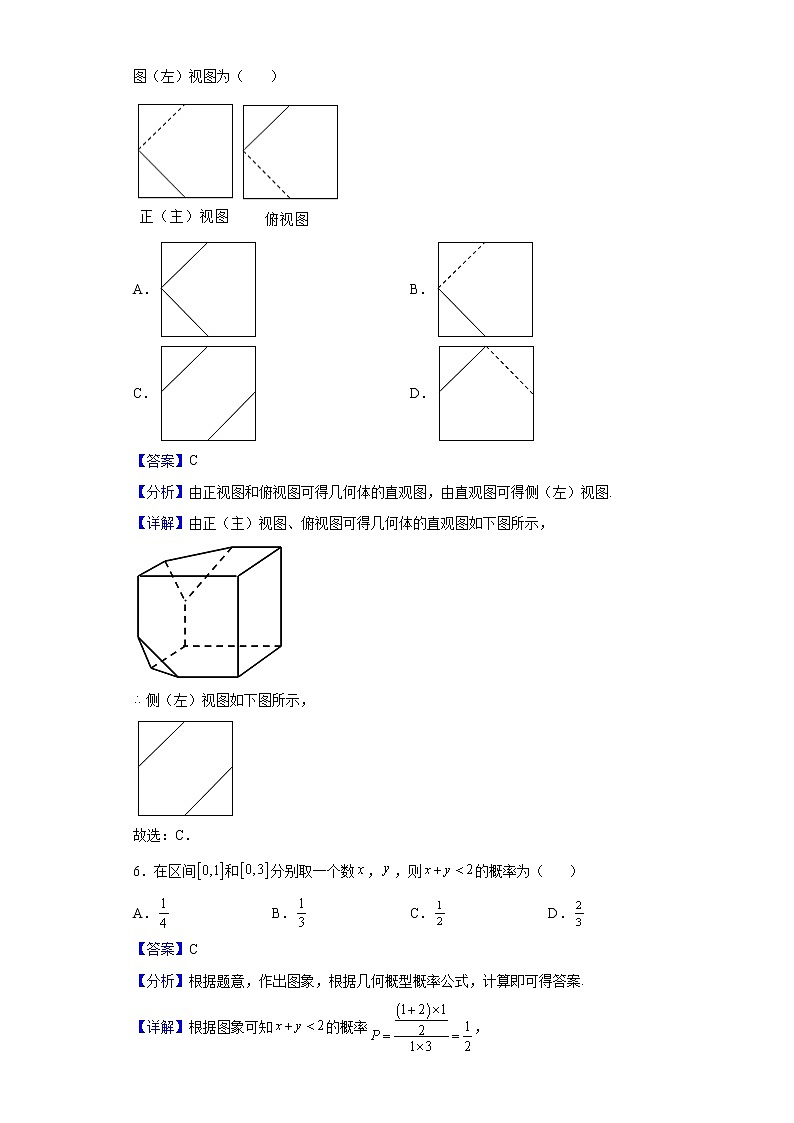
5．一个正方体截去两个角后所得几何体的正（主）视图、俯视图如图所示，则其侧视图（左）视图为（       ）

A． B．

C． D．

【答案】C

【分析】由正视图和俯视图可得几何体的直观图，由直观图可得侧（左）视图.

【详解】由正（主）视图、俯视图可得几何体的直观图如下图所示，

侧（左）视图如下图所示，

故选：C．

6．在区间和分别取一个数，，则的概率为（       ）

A． B． C． D．

【答案】C

【分析】根据题意，作出图象，根据几何概型概率公式，计算即可得答案.

【详解】根据图象可知的概率，

故选：C.

7．在中，，，，则的面积等于（       ）

A． B． C．或 D．或

【答案】D

【分析】先用余弦定理求出或2，进而利用三角形面积公式求出答案.

【详解】由余弦定理得：，解得：或2，经检验，均符合要求.

当时，；

当时，

故选：D

8．若直线被圆所截得的弦长为，则实数的值为（       ）

A．或3 B．或3 C．0或4 D．或6

【答案】C

【分析】利用直线和圆相交的弦长公式，直接求解实数的值.

【详解】解：由圆得圆心，半径，则圆心到直线的距离，

弦长，解得：或.

故选：C.

9．设，，，则a，b，c的大小关系为（       ）

A． B． C． D．

【答案】D

【分析】结合指数、对数函数单调性判断出大致范围，即可求解.

【详解】因为，，，

所以.

故选：D．

10．已知三棱锥的四个顶点在球的球面上，，是边长为的正三角形，三棱锥的体积为，则球的表面积为（       ）

A． B． C． D．

【答案】B

【分析】先根据条件可证明，，，故三棱锥放入正方体中，正方体的外接球即是三棱锥的外接球，从而即可求出球的半径，进而得到球的表面积．

【详解】设在底面上的射影为，如图，

因为，所以为的中心，

由题可知，，由，解得

在正中，可得.

从而直角三角形中解得.

进而可得，，，

因此正三棱锥可看作正方体的一角，

正方体的外接球与三棱锥的外接球相同，正方体对角线的中点为球心.

记外接球半径为，则，

所以，球的表面积为.

故选：B

11．设，是双曲线的左､焦点，在双曲线的一条渐近线上存在一点，使得三角形为等腰三角形，且，则双曲线的离心率为（       ）

A． B． C． D．

【答案】C

【分析】不妨假设点在渐近线上且在第一象限内，得出点的坐标，代入渐近线方程，结合得到答案.

【详解】因为为等腰三角形，且，所以，其中，

.不妨假设点在渐近线上且在第一象限内，过点作轴，交轴于点.

由题意,则 ，可得，

则，所以，

所以，故双曲线的离心率，

故选:C.

12．设函数的定义域为，满足，且当时，.若对任意，都有，则的取值范围是

A． B． C． D．

【答案】D

【解析】根据已知条件求出当时，函数，

做出示意图如下图所示： 要使，则需，而由可解得，从而得出的范围.

【详解】当时，，而时，所以

又，

所以当时，，

当时，，

做出示意图如下图所示：

要使，则需，而由解得，所以，

故选：D.

【点睛】本题考查函数不等式的求解问题，解决问题的关键在于根据已知条件求出相应区间的解析式，运用数形结合的思想巧妙求解不等式，属于中档题.

二、填空题

13．已知向量满足，，，则与的夹角为___________.

【答案】

【分析】利用坐标运算求得，根据数量积的运算律可求得，由此可得结果.

【详解】，，

，

解得：，又，.

故答案为：.

14．函数的图象在点处的切线方程为___________.

【答案】

【分析】利用导数的几何意义可得切线斜率，结合切点坐标可得切线方程.

【详解】由题意得：，，又，

所求切线方程为：，即.

故答案为：.

15．已知，是椭圆的两个焦点，P是椭圆E上任一点，则的取值范围是______．

【答案】

【分析】求出焦点坐标，设出（），利用向量的数量积的坐标表示和椭圆方程表达出，结合的取值范围，得到的取值范围.

【详解】由，，解得：，所以，

不妨令，，因为P是椭圆E上任一设点，设（），

则，即，其中

因为，所以，，

所以的取值范围是.

故答案为：

16．已知函数，若函数的图象在区间上的最高点和最低点共有个，下列说法正确的是___________.

①在上有且仅有个零点；

②在上有且仅有个极大值点；

③的取值范围是；

④在上为单递增函数.

【答案】②③

【分析】利用辅助角公式可化简得到，令，则，利用正弦函数图象可确定的范围，由此确定③正确；结合图象可知①②的正误；根据知④错误.

【详解】，

当时，，

令，则在上的最高点和最低点共有个，

由图象可知：需满足：，解得：，③正确；

当时，有且仅有个零点，即在上有且仅有个零点，①错误；

当时，有且仅有个极大值点，②正确；

当时，，则，

在上有增有减，④错误.

故答案为：②③.

【点睛】关键点点睛：本题考查正弦型函数图象与性质的相关应用，解题关键是能够将看做一个整体，采用换元法研究的图象，通过所需满足的范围确定范围及的性质.

三、解答题

17．某小区毗邻一条公路，为了解交通噪声，连续天监测噪声值（单位：分贝），得到频率分布直方图（图甲）.发现噪声污染严重，经有关部门在公路旁加装隔声板等治理措施后，再连续天监测噪声值，得到频率分布直方图（图乙）.把同一组中的数据用该组区间的中点值作代表，请解答下列问题：

(1)根据图乙估算出该小区治理后平均噪声值为分贝，估计治理后比治理前的平均噪声值降低了多少分贝？

(2)国家“城市区域环境噪声”规定：重度污染：分贝；中度污染：分贝；轻度污染：分贝；较好：分贝；好：分贝.把上述两个样本数据的频率视为概率，根据图甲估算出该小区噪声治理前一年内（天）噪声中度污染以上的天数为天，根据图乙估计一年内（天）噪声中度污染以上的天数比治理前减少了多少天？（精确到天）

【答案】(1)分贝；

(2)天.

【分析】（1）利用频率分布直方图估计平均数的方法可计算得到治理前的平均数，由此可得降低的分贝数；

（2）根据治理后中度污染以上的噪声值的频率可计算得到一年内的天数，由此可得减少的天数.

(1)

设治理前、后样本的平均值分别为，

，

又，，

治理后比治理前的平均噪声值降低了分贝；

(2)

由题意知：样本中度污染以上的噪声值在，

治理后，中度污染以上的频率为，

，则，

一年内，噪声中度污染以上的天数比治理前减少了天.

18．已知数列的前项和是，且，等差数列中，．

(1)求数列的通项公式；

(2)定义：记，求数列的前20项和．

【答案】(1)；

(2)

【分析】（1）利用求得递推关系得等比数列，从而得通项公式，再由等差数列的基本时法求得通项公式；

（2）根据定义求得，然后分组求和法求得和．

(1)

由题意，当时，．

两式相减，得，即．

是首项为3，公比为3的等比数列．

．

设数列的公差为，

．

．

(2)

由．

19．已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，.

（1）求三棱锥的体积；

（2）已知D为棱上的点，证明：.

【答案】(1)；(2)证明见解析.

【分析】（1）先证明为等腰直角三角形，然后利用体积公式可得三棱锥的体积；

（2）将所给的几何体进行补形，从而把线线垂直的问题转化为证明线面垂直，然后再由线面垂直可得题中的结论.

【详解】（1）由于，，所以，

又AB⊥BB1，，故平面，

则，为等腰直角三角形，

，.

（2）由（1）的结论可将几何体补形为一个棱长为2的正方体，如图所示，取棱的中点，连结，

正方形中，为中点，则，

又，

故平面，而平面，

从而.

【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积．对于空间中垂直关系（线线、线面、面面）的证明经常进行等价转化.

20．已知抛物线的焦点为F，A，B是该抛物线上不重合的两个动点，O为坐标原点，当A点的横坐标为4时，．

(1)求抛物线C的方程；

(2)以AB为直径的圆经过点，点A，B都不与点P重合，求的最小值．

【答案】(1)；

(2)11.

【分析】（1）作出辅助线，利用焦半径与余弦值求出的值，进而求出抛物线方程；（2）设出直线方程，与抛物线方程联立，根据得到等量关系，求出，从而表达出，求出最小值.

(1)

设，因为，所以，，过点A作AD⊥x轴于点D，则，，解得：，所以抛物线方程为.

(2)

设直线AB为，，由方程与联立得：，所以，即，且，，所以，，因为以AB为直径的圆经过点，所以，即，即，所以，所以，所以或，

当时，直线AB为过点P，此时与题干条件A，B都不与点P重合矛盾，不合题意，舍去；

当时，直线AB为，满足要求，所以，则，所以当时，最小，且最小值为11.

21．已知函数．

（1）若，求的单调区间；

（2）证明：只有一个零点．

【答案】（1）f（x）在（–∞，），（，+∞）单调递增，在（，）单调递减．

（2）见解析.

【详解】分析：（1）将代入，求导得，令求得增区间，令求得减区间；（2）令，即，则将问题转化为函数只有一个零点问题，研究函数单调性可得.

详解：（1）当a=3时，f（x）=，f ′（x）=．

令f ′（x）=0解得x=或x=．

当x∈（–∞，）∪（，+∞）时，f ′（x）>0；

当x∈（，）时，f ′（x）<0．

故f（x）在（–∞，），（，+∞）单调递增，在（，）单调递减．

（2）由于，所以等价于．

设=，则g ′（x）=≥0，仅当x=0时g ′（x）=0，所以g（x）在（–∞，+∞）单调递增．故g（x）至多有一个零点，从而f（x）至多有一个零点．

又f（3a–1）=，f（3a+1）=，故f（x）有一个零点．

综上，f（x）只有一个零点．

点睛：（1）用导数求函数单调区间的步骤如下：①确定函数的定义域；②求导数；③由（或）解出相应的的取值范围，当时，在相应区间上是增函数；当时，在相应区间上是减增函数.

（2）本题第二问重在考查零点存在性问题，解题的关键在于将问题转化为求证函数有唯一零点，可先证明其单调，再结合零点存在性定理进行论证.

22．在直角坐标系中，曲线的参数方程为：（为参数）.以坐标原点为极点，以轴正半轴为极轴建立极坐标系，直线的极坐标方程为：（）

（1）求曲线的普通方程和直线的直角坐标方程；

（2），直线与曲线相交于，两点，若，求.

【答案】（1），，；（2）.

【分析】（1）消去参数可得曲线的普通方程为；利用两角差的正弦公式化简，再根据直角坐标与极坐标的互化公式可得线的直角坐标方程；

（2）将直线的参数方程为为参数）代入，利用参数的几何意义可求出结果.

【详解】（1）由曲线的参数方程消去参数得曲线的普通方程为

由直线的极坐标方程为：，

得，

整理得，

所以，

所以直线的直角坐标方程为，,

（2）由（1）得，直线的参数方程为为参数）代入，

整理得，，

设点，对应的参数分别为，，

则，①     ，②

因为，则，且，，

即，③

① ③联立，得，.

代入②式整理得，

所以.

【点睛】关键点点睛：掌握参数方程化普通方程、直角坐标与极坐标的互化公式以及直线参数方程中参数的几何意义是解题关键.

23．记函数的最小值为．

(1)求的值；

(2)若正数满足，证明：．

【答案】(1);

(2)证明见解析；

【分析】（1）将函数化简为分段函数形式，并作出函数图像，由图像判断并计算最小值；（2）由（1）得，可得，将证明不等式转化为证明成立，利用柯西不等式证明即可.

(1)

由题意得，，作出函数图像如图所示，由图可知，当时，函数取最小值，，故.

(2)

由（1）得，故，因为均为正数，所以要证明不等式，只需证明，由柯西不等式得：，当且仅当时，取等号，所以原不等式成立.

【点睛】函数中有绝对值形式的情况，一般在求解时需要去绝对值，转化为分段函数，并作出图像，数形结合分析求解.