
浙教版数学七下期末复习阶梯训练:数据与统计图表(优生集训)含解析
展开这是一份浙教版数学七下期末复习阶梯训练:数据与统计图表(优生集训)含解析,共21页。试卷主要包含了综合题等内容,欢迎下载使用。
浙教版数学七下期末复习阶梯训练:数据与统计图表(优生集训)
一、综合题
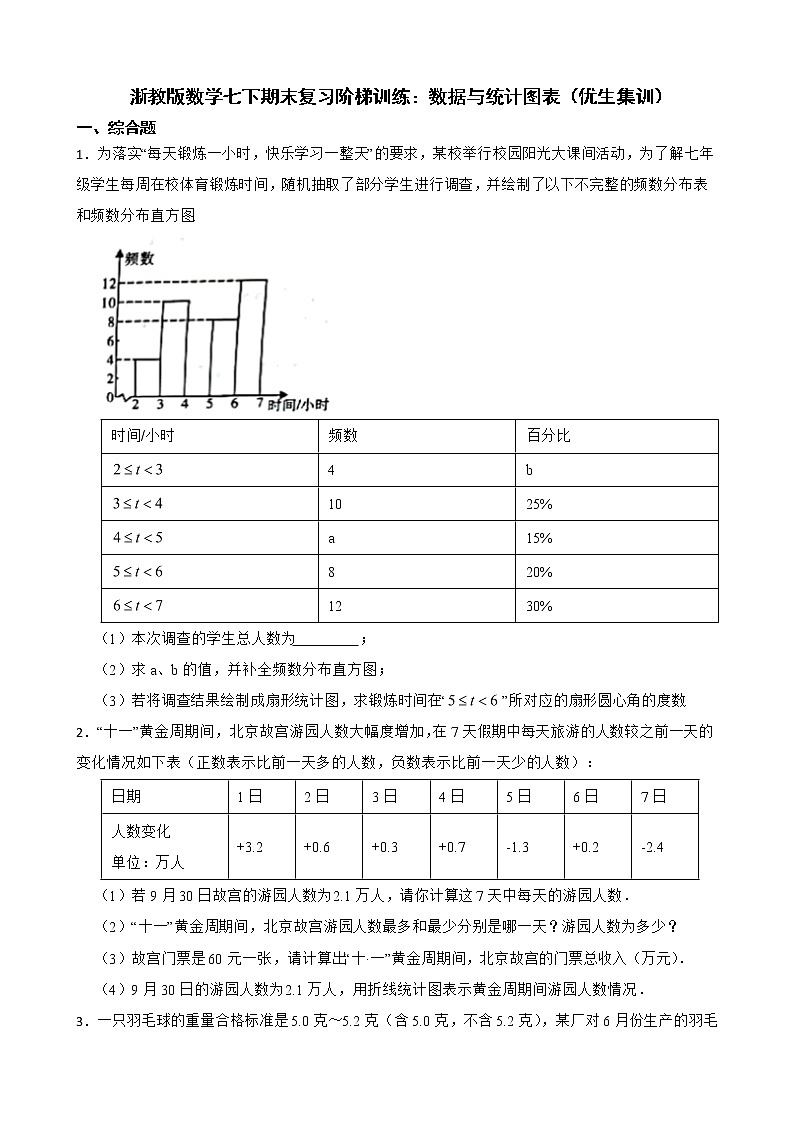
1.为落实“每天锻炼一小时,快乐学习一整天”的要求,某校举行校园阳光大课间活动,为了解七年级学生每周在校体育锻炼时间,随机抽取了部分学生进行调查,并绘制了以下不完整的频数分布表和频数分布直方图.
时间/小时
频数
百分比
4
b
10
25%
a
15%
8
20%
12
30%
(1)本次调查的学生总人数为 ;
(2)求a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求锻炼时间在“”所对应的扇形圆心角的度数.
2.“十一”黄金周期间,北京故宫游园人数大幅度增加,在7天假期中每天旅游的人数较之前一天的变化情况如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化
单位:万人
+3.2
+0.6
+0.3
+0.7
-1.3
+0.2
-2.4
(1)若9月30日故宫的游园人数为2.1万人,请你计算这7天中每天的游园人数.
(2)“十一”黄金周期间,北京故宫游园人数最多和最少分别是哪一天?游园人数为多少?
(3)故宫门票是60元一张,请计算出“十·一”黄金周期间,北京故宫的门票总收入(万元).
(4)9月30日的游园人数为2.1万人,用折线统计图表示黄金周期间游园人数情况.
3.一只羽毛球的重量合格标准是5.0克~5.2克(含5.0克,不含5.2克),某厂对6月份生产的羽毛球重量进行抽样检验,并将所得数据绘制成如图统计图表.
6月份生产的羽毛球重量统计表
组别
重量x(克)
数量(只)
A
x<5.0
a
B
5.0≤x<5.1
480
C
5.1≤x<5.2
660
D
x≥5.2
30
(1)求表中a的值及图中B组扇形的圆心角的度数;
(2)这些抽样检验的羽毛球中,合格率是多少?如果购得6月份生产的羽毛球15筒(每筒12只),估计所购得的羽毛球中,非合格品的羽毛球有多少只?
4.为了解某校七年级学生的跳高水平,随机抽取该年级60名学生进行跳高测试,并把测试成绩分成四组,绘制成如图所示的频数表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级60名学生跳高测试成绩的频数表:
组别(m)
频数
1.09~1.19
8
1.19~1.29
16
1.29~1.39
a
1.39~1.49
12
(1)求a的值;
(2)把频数分布直方图补充完整;
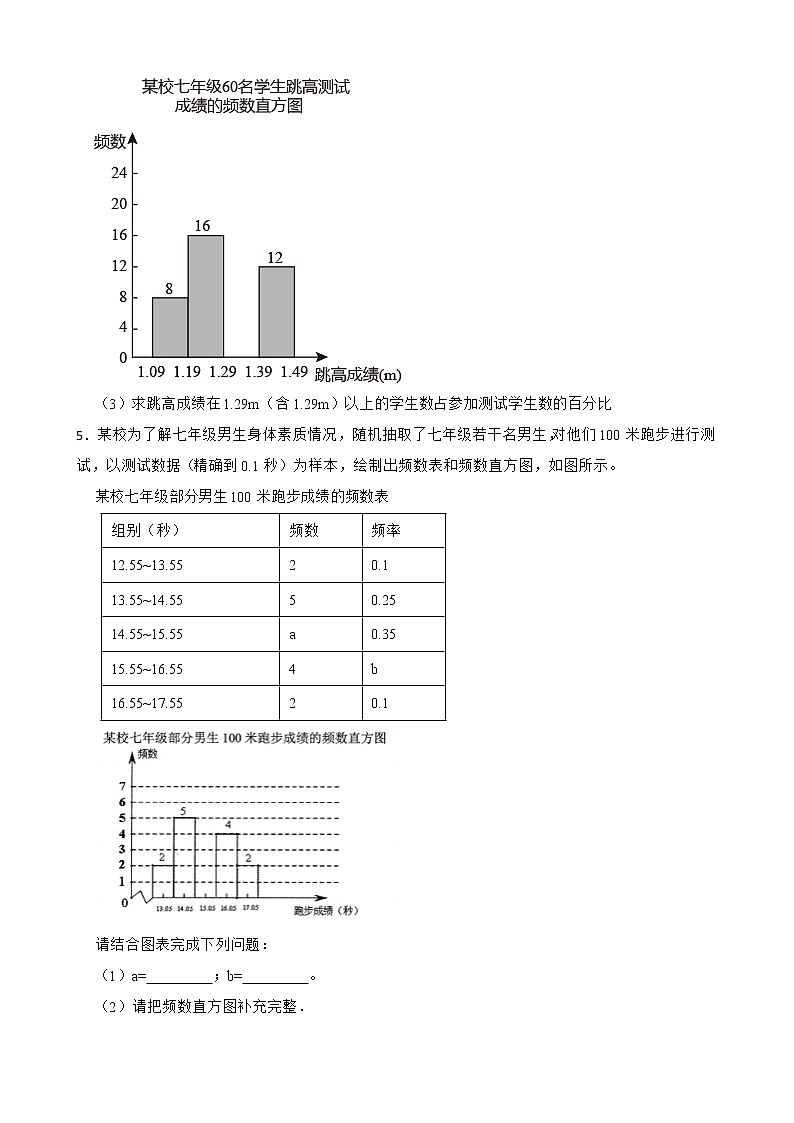
(3)求跳高成绩在1.29m(含1.29m)以上的学生数占参加测试学生数的百分比.
5.某校为了解七年级男生身体素质情况,随机抽取了七年级若干名男生,对他们100米跑步进行测试,以测试数据(精确到0.1秒)为样本,绘制出频数表和频数直方图,如图所示。
某校七年级部分男生100米跑步成绩的频数表
组别(秒)
频数
频率
12.55~13.55
2
0.1
13.55~14.55
5
0.25
14.55~15.55
a
0.35
15.55~16.55
4
b
16.55~17.55
2
0.1
请结合图表完成下列问题:
(1)a= ;b= 。
(2)请把频数直方图补充完整.
(3)若100米跑步成绩为15.5秒或小于15.5秒为优秀,七年级男生共有150名,请估计七年级男生100米跑步成绩达到优秀的人数。
6.某校七年级英语演讲比赛结束后,老师对比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
(1)问该校共有多少名学生参加此次英语演讲比赛?
(2)分数在“89.5~94.5”的学生有多少名?
7.我市为响应国家“低碳环保,绿色出行”的号召,投放“共享单车”供市民出行时租用.寒假期间,七年级数学兴趣小组对某投放点的租车情况进行一周的调查,并把收集的数据绘制成下面的频数分布直方图和扇形统计图:
(1)根据统计图提供的信息,估算这个站点一周的租车总次数是多少次;
(2)补全频数分布直方图;
(3)求周三租车次数所在扇形的圆心角度数.
8.体育老师统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数
60≤x<80
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
频数
4
13
19
7
5
2
请你结合表中所给信息解答下列问题:
(1)全班有 名学生;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范国的学生占全班学生的 %;
(4)请把频数分布直方图补充完整.
9.小李调查了本班50名同学各自家庭的人均日用水量(单位:升)
收集数据如下:
55 42 50 48 42 35 38 39 40 51 47 52 50 42 43 47 52 48
52 38 42 60 52 41 46 35 47 53 48 52 47 50 49 57 43 40
44 52 50 49 37 46 42 62 58 46 48 39 60 54
整理数据:列频数分 布表如下(不完整)
组别
人均日用水量(x)
划记
频数(家庭数)
A
35≤x<39
5
B
39≤x<43
10
C
43≤x<47
6
D
47≤x<51
14
E
51≤x<55
9
F
55≤x<59
G
59≤x<63
3
合计
50
50
描述数据:画频数分布直方图和扇形统计图如右图
根据以上信息,解答下列问题:
(1)请分别补全频数分布表、频数分布直方图和扇形统计图;
(2)求D组数据所对应的扇形统计图的圆心角度数;
(3)①家庭的人均日用水量在哪个范围的频数最多?
②小李为了在班级上提倡节约用水,而且使班级中70%的家庭不受影响,他应该倡议家庭的人均日用水量不超过多少升比较合适?(取正整数值,不用说明理由)
10.为丰富学生的课余生活,培养学生的爱好,陶冶学生的情操,某校开展学生拓展课,为了解学生各社团活动的参与人数,该校对社团活动进行了抽样调查,制作出如下的统计图。根据该统计图,完成以下问题:
(1)这次共调查了 名学生
(2)请把统计图1补充完整。
(3)已知该校七年级共有680名学生参加社团活动,请根据样本估算该校七年级学生参加艺术类社团的人数
11.体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
次数
频数
2
18
13
8
1
(1)补全频数分布表和频数分布直方图.
(2)上表中组距是 次,组数是 组.
(3)跳组次数在 范围的学生有 人,全班共有 人.
(4)若规定跳维次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
12.为了解某县2020年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
成绩等级
A
B
C
D
人数
60
10
百分比
30%
50%
15%
m
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 名;
(2)表中 , 和 所表示的数分别为: = , = , = ;
(3)请补全条形统计图;
(4)若将抽取的若干名学生的实验成绩绘制成扇形统计图,则实验成绩为D类的扇形所对应的圆心角的度数是多少.
13.近年来,随着人们健康睡眠的意识不断提高,社会各界对于初中生的睡眠时间是否充足越发关注,近日某学校从全校1600人中随机抽取了部分同学,调查他们平均每日睡眠时间,将得到的数据整理后绘制了如图所示的不完整的扇形统计图和频数分布直方图:
(1)本次接受调查的人数为 ;
(2)补全直方图;
(3)教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出,初中生睡眠时间应达到9小时,试估计该校学生睡眠时间达标人数,并评价该校初中生睡眠时间情况.
14.宁波市海曙区总工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图所示的不完整统计图.
(1)被调查员工人数为 人:
(2)把条形统计图补充完整;
(3)若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
15.对若干只电灯泡的使用寿命进行检测,得到如图的频数分布直方图(每一组含前一个边界值,不含后一个边界值).请根据这个直方图回答下列问题.
(1)被检测的电灯泡共有多少只?
(2)直方图中的组距为多少?
(3)使用寿命在550小时以上(含550小时)的灯泡有多少只?占被检测灯泡总数的百分之几?
16.随着手机的日益普及,学生使用手机对学校管理和学生发展带来诸多影响.今年2月1日,教育部发布《关于加强中小学生手机管理工作的通知》.某学校为了解该校学生使用手机的主要用途,随机调查了该校的部分学生,并根据调查结果整理制作了如下尚不完整的统计图,请根据调查的相关信息解答下列问题:
(1)求出参与本次调查的学生人数;
(2)补全条形图,并求出圆心角α的度数;
(3)如果随机在该校询问一名学生,求该名学生使用手机的主要用途为“在线学习”或“查资料”的概率是多少.
17.某市学校有5类,各类学校占总学校数量的百分比如下:
学校类别
中学
小学
幼儿园
特殊教育学校
高等院校
百分比
22%
32%
36%
4%
6%
(1)计算各类学校对应的扇形圆心角度数(结果精确到1°).
(2)画扇形统计图来表示上面的信息.
(3)哪两类学校较多?占总学校数量的百分比各是多少?
18.为贯彻落实教育部印发的《大中小学劳动教育指导纲要(试行)》通知要求,培养学生劳动习惯与劳动能力,某校学生发展中心在暑假期间开展了“家务劳动我最行”的实践活动,开学后从校七至九年级各随机抽取30名学生,对他们的每日平均家务劳动时长(单位:min)进行了调查,并对数据进行了收集、整理和描述.下面是其中的部分信息:
a.90名学生每日平均家务劳动时长的频数分布表:
分组
频数
20≤x<25
9
25≤x<30
m
30≤x<35
15
35≤x<40
24
40≤x<45
n
45≤x<50
9
合计
90
b.90名学生每日平均家务劳动时长频数分布直方图:
c.每日平均家务劳动时长在35≤x<40这一组的是:
35 35 35 35 36 36 36 36 36 37 37 37
38 38 38 38 38 38 38 39 39 39 39 39
d.小东每日平均家务劳动时长为37min.
根据以上信息,回答下列问题:
(1)写出频数分布表中的数值m= ,n= ;
(2)补全频数分布直方图;
(3)小东每日平均家务劳动时长 样本中一半学生的每日平均家务劳动时长;(填“超过”或“没超过”)
(4)学生发展中心准备将每日平均家务劳动时长达到40min及以上的学生评为“家务小能手”,如果该校七至九年级共有420名学生,请估计获奖的学生人数.
19.为庆祝中国共产党建党100周年,使学生进一步了解中国共产党的历史,某学校组织了“党史百年天天读”活动,并进行了一次全校2000名学生都参加的书面测试,阅卷后,教学处随机抽取了100份答卷进行分析统计,发现考试成绩x(分)的最低分为50分,最高分为满分100分,且分数都为整数,并绘制了尚不完整的统计图表:
分数段(x分)
频数
频率
50≤x<60
4
0.04
60≤x<70
a
0.20
70≤x<80
30
0.30
80≤x<90
26
b
90≤x<100
15
0.15
100≤x<110
5
0.05
请根据统计图表提供的信息,解答下列问题:
(1)在频数分布表中,a= ;b= ;
(2)请将频数分布直方图补充完整,并在图中标明相应数据;
(3)该校对成绩为90≤x≤100的学生进行奖励,按成绩从高分到低分设一,二,三等奖,各奖项的人数占比如扇形统计图所示.
① 在扇形图中,二等奖所在扇形的圆心角度数为 °;
② 请你估算全校获得一等奖的学生人数约为 人.
20.为了解某校学生在五一假期阅读的情况,随机抽取了若干名学生进行调查,获得他们的阅读时间(单位:h),并对数据(时间)进行整理、描述.下面给出了部分信息:图1是阅读时间频数分布直方图(数据分成5组:2≤t<4,4≤t<6,6≤t<8,8≤t<10,10≤t≤12),图2是阅读时间扇形统计图.
根据以上信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)补全图1;
(3)图2中,2≤t<4所在的扇形的圆心角的度数是 ;
(4)已知该校共有1800名学生,估计该校学生在五一假期阅读时间不少于6h的人数.
21.报纸上刊登了一则新闻,标题为“保健食品合格率为75%”,请据此回答下列问题.
产地
国内
进口
被检数
55
5
不合格数
14
1
(1)这则新闻能否说明市面上所有保健食品中恰好有25%的为不合格产品?
(2)你认为这则消息来源于普查,还是抽样调查?为什么?
(3)如果已知在这次检查中各项指标均合格的商品有45种,你能算出共有多少种保健食品接受检查了吗?
(4)此次检查的结果如下表,有人由此认为“进口商品的不合格率较低,更让人放心.”你同意这种说法吗?为什么?
22.建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行 元钱.
(2)请判断在这七次办理业务中,小张在第 次业务办理后手中现金最多,第 次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
23.某商场对今年中秋节这天销售A、B、C三种品牌的月饼情况进行了统计,绘制了如图所示的条形和扇形统计图.根据图中信息解答下列问题:
(1)哪一种品牌月饼的销售量最大?
(2)写出A品牌月饼在扇形统计图所对应的圆心角的度数.
(3)根据上述统计信息,明年中秋节期间该商场对A、B、C三种品牌的月饼如何进货?请你提一条合理化的建议.
24.九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
分数段(分)
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~99.5
组中值(分)
54.5
64.5
74.5
84.5
94.5
频数
a
9
10
14
5
所占百分比
5%
22.5%
25.0%
35.0%
b
(1)频数分布表中a= ,b= ;
(2)画频数分布直方图;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
25.为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了 名学生;
(2)请补全两幅统计图;
答案解析部分
【解析】【解答】解:(1)∵体育锻炼时间“3≤t<4”频数10,百分比是25%,
∴学生总人数为10÷25%=40;
故答案为 :40;
【分析】(1)利用统计表可知学生总人数=体育锻炼时间“3≤t<4”的频数÷其百分比,列式计算;
(2)利用表中数据,利用各组频数之和等于调查的总人数可求出a的值;利用频数÷总人数=百分比,列式计算求出b的值,然后补全频数分布直方图;
(3)根据锻炼时间在“5≤t<6”所对应的扇形圆心角的度数=360°×体育锻炼时间“5≤t<6”的人数所占的百分比,列式计算可求出结果.
【解析】【分析】(1)根据表格中所给的数据计算求解即可;
(2)根据(1)中所求求解即可;
(3)求出 60×(5.3+5.9+6.2+6.9+5.6+5.8+3.4)=2346 即可作答;
(4)根据(1)中所求的数据作图即可。
【解析】【分析】(1)利用C组的频数除以其百分比,即得样本容量,再根据各组频数之和等于样本容量,求出a即可;利用B组百分比乘以360°,即得B组扇形的圆心角的度数;
(2)利用C、D两组频数之和除以样本容量,再乘以100%即得合格率;利用6月份生产的羽毛球的总只数乘以样本中的不合格率即得结论.
【解析】【分析】(1)利用各组频数之和等于样本容量,即可求出a值;
(2)利用(1)结论补图即可;
(3) 利用样本中跳高成绩在1.29m(含1.29m)以上的学生人数除以样本容量,再乘以100%即可.
【解析】【解答】解:(1)抽取的人数为2÷0。1=20
∴a=20-2-5-4-2=7.
∴b=4÷20=0.2.
故答案为:7,0.2
【分析】(1)利用频数÷频率=总数,可求出抽取的人数,再求出a的值;再利用频率=频数÷抽取的人数,可求出b的值.
(2)利用a的值补全频数分布直方图.
(3)利用七年级男生的人数×成绩达到优秀的人数所占的百分比,列式计算可求解.
【解析】【分析】(1)利用条形统计图和扇形统计图,可求出结果.
(2)利用学校参加此次英语演讲比赛的人数×成绩在“69.5~79.5”组的人数所占的百分比,列式计算可求出成绩在“69.5~79.5”组的人数;再分别求出成绩在69.5~74.5” 组的人数,即可求出成绩在“89.5~94.5”组的人数.
【解析】【分析】(1)利用第五周的次数除以所占的比例可得总次数;
(2)根据总次数可得周日的次数,据此补全频数分布直方图;
(3)利用第三周的次数除以总次数,然后乘以360°即可.
【解析】【解答】解:(1)全班学生人数为: (人 ;
(2)组距是20,组数是6;
(3)跳绳次数 在 范围的学生占全班学生的百分比为 ,
故答案是:52;
【分析】(1)根据频数分布表的数据进行计算即可;
(2)根据频数分布表的数据进行判断即可;
(3)根据频数分布表的数据进行计算即可;
(4)根据频数分布表的数据,画出频数分布直方图即可。
【解析】【分析】(1)分析图表结合题意即可解答;
(2)根据圆心角的计算公式即可解答;
(3)①观察图表即可解答;
②观察图表并求出70%的人数即可解答.
【解析】【解答】解:(1)由题意得:32÷40%=80(名),
故答案为:80.
(2)B=80-32-24-8=16(人).
【分析】(1)运用总人数=A的人数÷A所占百分比即可求解;
(2)先用总人数减去A、C、D的人数求出B的人数,再画图即可;
(3)用总人数× 艺术类社团所占的百分比即可求解.
【解析】【解答】解:(2)上表中组距是80-60=20(次),组数为7组;(3)跳绳次数在100≤x<120范围的学生有18人,全班共有2+4+18+13+8+4+1=50(人);
(4)
故答案为(1)4,4,见解析;(2)20,7;(3)18,50;(4)全班同学跳绳的优秀率是 .
【分析】(1)结合条形统计图及表格补全频数分布表和频数分布直方图即可;
(2)求出上表中的组距,以及组数即可;
(3)找出跳绳次数在100 ≤ x<120范围的学生数,求出全班的人数即可;
(4)找出成绩不低于140次的人数,除以总人数即可求出优秀率。
【解析】【解答】解:(1)由题意可得,
本次抽查的学生有: (名 ,
故答案为:200;
(2)由(1)可知本次抽查的学生有200名,
, , ,
故答案为:100,30, ;
【分析】(1)利用A的人数除以百分比即可求出总人数;
(2)用总人数乘以B的百分比即可求出x,再用总人数乘以C的白分式即可求出y,再用D的人数除以总人数即可求出m;
(3)根据(2)的结果直接作图即可;
(4)利用D的白分式乘以360度即可得出答案。
【解析】【解答】解:(1)由题意得27÷27%=100(人),
故答案为:100;
【分析】(1)根据样本÷所占百分比=总体即可求解;
(2)求出睡眠8≤t≤9的人数再画图即可求解;
(3)根据样本中睡眠时间“达标”人数所占的百分比乘以总人数即可计算出该校学生睡眠达标的人数,再根据达标率进行判断即可求解.
【解析】【解答】(1)解:40050%=800.
【分析】(1)求总人数可以用不剩的人数除以他的占比.
(2)总人数减去其他类型人数即可.
(3)计算出剩少量人数占比,再计算10000人里面数量.
【解析】【分析】(1)求各组频数之和即可;
(2)将每组的最大值减去最小值即得结果;
(3)将第三组合第四组的频数相加即可;再利用频率=频数÷总数可得其占被检测灯泡总数的百分比.
【解析】【分析】(1)利用在线学习的人数除以所占的比例可得总人数;
(2)根据总人数求出查资料的人数,据此补全条形统计图,利用娱乐的人数除以总人数,然后乘以360°可得娱乐所在扇形圆心角的度数;
(3)利用在线学习以及查资料的人数和除以总人数可得对应的概率.
【解析】【分析】(1)根据表格中各类学校所占的百分比,求出各类学校对应的扇形圆心角度数即可;
(2)根据题意画出扇形统计图即可;
(3)根据表格中的数据可直接得出结论。
【解析】【解答】解:(1)由频数分布直方图得: ,
,
故答案为:12,21;
(2)根据 补全频数分布直方图如下:
(3)在 这一组内,每日平均家务劳动时长达到 及以上的学生人数为15人,
则在样本中,每日平均家务劳动时长达到 及以上的学生人数为 (人),
因此,每日平均家务劳动时长低于37min的人数为45人,故小东每日平均家务劳动时长超过了样本中一半学生的每日平均家务劳动时长,
故答案为:超过;
【分析】(1)由频数分布直方图可得m的值,再由各组人数之和等于总人数可得n的值;
(2)根据以上所求结果可补全图形;
(3)计算出样本中后45个数据的平均数,再比较即可得出答案;
(4)用总人数乘以样本中5、6组人数所占比例即可。
【解析】【解答】解:(1) ; ,
故答案为:20;0.26;
(3)① ,
故答案为:108;
② ,
故答案为:40.
【分析】(1)先计算出样本容量,再根据频率=频数➗样本容量求解即可;
(2)根据以上所求结果即可补全图形;
(3)①用360°乘以对应的百分比即可;②用总人数乘以 90≤x≤100的学生人数所占比例,再乘以一等奖对应的百分比即可。
【解析】【解答】解:(1)样本容量:24÷25%=96;
(3)图2中,2≤t<4所在的扇形的圆心角的度数是:8÷96×360°=30°;
【分析】(1)由4≤t<6的人数及其所占百分比可得样本容量;
(2)根据各组人数之和等于总人数求解可得8≤t<10的人数;
(3)用360°乘以2≤t<4人数所占比例即可;
(4)用总人数乘以样本中阅读时间不少于6小时的人数所占比例即可。
【解析】【分析】(1)根据表格中的数据求解即可;
(2)根据抽样调查的特点求解即可;
(3)求出 =60 即可作答;
(4)求出 进口商品被检数太少,即样本容量太小,不能反映总体水平即可作答。
【解析】【解答】解:1)下班时应交回银行:4000+2000-800+400-800+1400-1700-200=4300(元).(2)+2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
第一次:2000元;第二次:2000-800=1200元;第三次:1200+400=1600元;第四次:1600-800=800元;第五次:800+1400=2200元;第六次:2200-1700=500元;第七次:500-300=200元;
∴小张在第五次办理业务后,手中的现金最多;第七次办理业务后,手中的现金最少.
故答案为:五,七.
【分析】(1)他办理的七笔业务的数据相加,在加上4000元既得下班时应交回银行的钱数.(2)根据所给的数据直接计算比较可得在第五次业务办理后手中现金最多,第七次业务办理后手中现金最少.(3)求出七笔业务给出的数据的绝对值的和,在乘以0.1%即可.(4)根据他办理的七笔业务的数据,先描点,在用线段连接即可得折线图.
【解析】【分析】(1)根据扇形统计图即可得销售量最大的牛奶品牌.(2)先求出A品牌牛奶所占的百分比,再与360°相乘即可求出在扇形中所对应的圆心角的度数.(3)由两个统计图都可看出多进C,少进A,适量进B.
【解析】【分析】(1)由成绩频数分布表可以看出,b=1-0.05-0.225-0.25-0.35=0.125;由已知组的频数占总数的百分比及频数求出总数,用总数乘0.050求出a的值;(2)由数据补全直方图;(3)由表得,有29名同学获得一等奖或二等奖;设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得关系式15x+10(29-x)=335可求得x的值;再根据关系式50x+30(29-x)可求得获得的奖金.
【解析】【分析】(1)根据A类的人数和所占的百分比,求出总人数;(2)用整体1减去A、C、D类所占的百分比,求出B所占的百分比;用总人数乘以所占的百分比,求出C的人数,由此补全图形.
相关试卷
这是一份浙教版数学七下复习阶梯训练:数据与统计图表(优生加练)含解析,共14页。试卷主要包含了单选题,填空题,解答题,综合题等内容,欢迎下载使用。
这是一份浙教版数学七下复习阶梯训练:因式分解(优生集训)含解析,共9页。试卷主要包含了综合题等内容,欢迎下载使用。
这是一份浙教版数学七下复习阶梯训练:整式的乘除(优生集训)含解析,共22页。试卷主要包含了综合题等内容,欢迎下载使用。












