2022年江苏省常州市第二十四中学&河海中学中考数学（一模）试题（有答案）

九年级教学情况调研测试2022.5

数学试题

一、选择题（本大题共8小题，每小题2分，共16分，在每小题所给出的四个选项中，只有一项是正确的.）

1．2022年冬奥会在北京举行，以下历届冬奥会会徽是轴对称图形的是（    ）

A． B． C． D．

2．下列运算正确的是（    ）

A． B． C． D．

3．下列四个几何体中，三视图都是相同图形的是（    ）

A． B． C． D．

4．王老师为了了解本班学生每周课外阅读时间，抽取了10名同学进行调查，调查结果统计如下：

那么这组数据的中位数和众数分别是（    ）

A．4，4 B．5，4 C．5，5 D．都无法确定

5．中国疫苗撑起全球抗疫“生命线”！预计2022年中国新冠疫苗产能有望达到50亿剂，约占全球产能的一半，必将为全球抗疫作出重大贡献。数据“50亿”．用科学记数法表示为（    ）

A． B． C． D．

6．若点在的图像上，且，则b的取值范围为（    ）

A． B． C． D．

7．如图，AB是的直径，点C在上，，垂足为D，点E是上的动点（不与C重合），点F为CE的中点，若，，则DF的最大值为（    ）

A．2 B． C．5 D．10

8．如图1，在中，，点E为BC的中点，点P沿BC从点B运动到点C．设B，P两点间的距离为x，，图2是点P运动时y随x变化的关系图象，则BC的长为（    ）

A．3 B．4 C．5 D．6

二、填空题（本大题共10小题5，每小题2分，共20分.）

9．计算：______．

10．若二次根式有意义，则x的取值范围是______．

11．分解因式：______．

12．正五边形的每个外角=______°．

13．若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则圆锥的侧面积是______．

14．一次函数的值随x值的增大而减少，则常数a的取值范围是______．

15．如图，将绕点A按逆时针方向旋转100°，得到，若点在线段BC的延长线上，则______．

16．如图，四边形ABCD是平行四边形，其中边AD是的直径，BC与相切于点B，若的周长是，则四边形ABCD的面积为______．

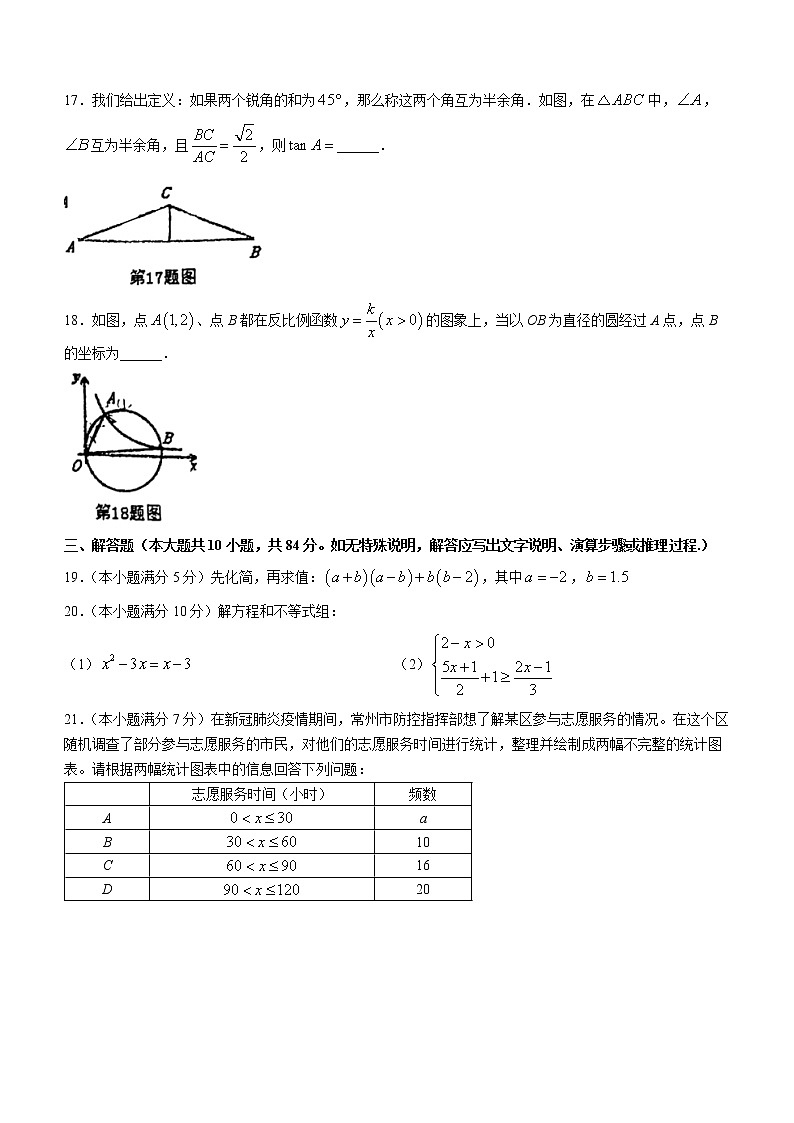
17．我们给出定义：如果两个锐角的和为，那么称这两个角互为半余角．如图，在中，，互为半余角，且，则______．

18．如图，点、点B都在反比例函数的图象上，当以OB为直径的圆经过A点，点B的坐标为______．

三、解答题（本大题共10小题，共84分。如无特殊说明，解答应写出文字说明、演算步骤或推理过程.）

19．（本小题满分5分）先化简，再求值：，其中，

20．（本小题满分10分）解方程和不等式组：

（1） （2）

21．（本小题满分7分）在新冠肺炎疫情期间，常州市防控指挥部想了解某区参与志愿服务的情况。在这个区随机调查了部分参与志愿服务的市民，对他们的志愿服务时间进行统计，整理并绘制成两幅不完整的统计图表。请根据两幅统计图表中的信息回答下列问题：

（1）本次被抽取的市民共有______名：

（2）表中a=______，扇形统计图中“C”部分所占百分比为______；

（3）扇形统计图中，“D”所对应的扇形圆心角的度数为______°；

（4）若该区共有30000名参与志愿服务的市民，那么志愿服务时间多于60小时的市民大约有多少人？

22．（本小题满分8分）常州市某学校疫情居家学习期间，各班网络课程每天下午只安排三节课。八年级（1）班星期二下午安排了数学、体育、生理课各一节。

（1）安排第一节是数学课的概率=______；

（2）求把数学课安排在最后一节的概率。

23．（本小题满分8分）如图，在中，，点D，E分别是BC，AB上的中点，连接DE并延长至点F，使，连接CE，AF．

（1）证明：

（2）当时，试判断四边形ACEF的形状并说明理由。

24．（本小题满分8分）2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢。某商家两次购进冰墩墩进行销售，第一次用22000元，。很快销售一空，第二次又用48000元购进同款冰墩墩，所购进数量是第一次的2倍，但单价贵了10元。

（1）求该商家第一次购进冰墩墩多少个？

（2）若所有冰墩墩都按相同的标价销售，要求全部销售完后的利润率不低于20%（不考虑其他因素），那么每个冰墩墩的标价至少为多少元？

25．（本小题满分8分）如图，在中，，轴，垂足为D，边AB所在直线分别交x轴、y轴于点E、F，且，反比例函数的图像经过A、C两点，已知点．

（1）求AB所在直线对应的函数表达式；

（2）求点C的坐标．

26．（本小题满分10分）请阅读下列科普材料，并完成相应的任务。

图算法是根据几何原理，将某一已知函数关系式中的各变量，分别编成有刻度的直线（或曲线），并把它们按一定的规律排列在一起的一种图形，可以用来解函数式中的未知量。比如想知道10摄氏度相当于多少华氏度，我们可根据华氏温度F与摄氏温度C之间的关系：得出，当时，.但是如果你的温度计（如图①）上有华氏温标刻度，就可以从温度计上直接读出答案，这种利用特制的线条进行计算的方法就是图算法。

再看一个例子：如图②，设有两只电阻，千欧，千欧，问并联后的总电阻值R是多少千欧？

我们可以利用公式：求得R的值，也可以设计一种图算法（如图③）直接得出结果：我们先来画出一个120°的角，再画一条角平分线，在角的两边及角平分线上用同样的单位长度进行刻度，这样就制好了一张算图。我们只要把角的两边刻着千欧和千欧的两点连成一条直线，这条直线与角平分线的交点的刻度值就是并联后的总电阻值R．

图算法得出的数据大多是近似值，但在大多数情况下是够用的，那些需要用同一类公式进行计算的测量制图人员，往往更能体会到它的优越性。

任务：

（1）请根据以上材料简要说出图算法的优越性：

（2）①用公式计算：当千欧，千欧时，的值为多少千欧?

②如图③，，OC是的角平分线，，，，用你所学的几何知识说明：．

27．（本小题满分10分）在平行四边形ABCD中，对角线AC与边CD垂直，，点E是AD延长线上的一点，点F是射线AB上的一点，且．

（1）如图1，如果点F与点B重合，则的余弦值=______

（2）如图2，若四边形ABCD的周长是16，设，，

①求y关于x的函数关系式并写出自变量x取值范围；

②若，求的面积．

28．（本小题满分10分）定义：有一条边等于这条边上高的两倍的三角形叫做底倍高三角形，这条边叫做这个三角形的倍底．

（1）概念理解：

请你根据上述定义举一个底倍高三角形的例子：______；

（2）问题探究：在平面直角坐标系xOy中，抛物线过点，点，

△ABC是以AB为倍底的底倍高三角形．

①直接写出点C所在图形的函数关系式；

②设点P是抛物线位于AB上方任意一点，当PC取最小值时，求点C的坐标；

（3）应用拓展：

在（2）的条件下，已知的半径为1，圆心I在直线上，且点C在上，设圆心I的横坐标为t，试直接写出t的取值范围．