2022新疆昌吉学联体高三第三次高考适应性联考文数Word含答案

2021-2022年昌吉学联体第三次高三年级高考适应性考试

文科数学试卷

一､选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. （    ）

A.  B.  C.  D.

2. 已知集合，，则（    ）

A.  B.  C.  D.

3. 设等差数列的前n项和为，且，，则（    ）

A. 60 B. 90 C. 120 D. 180

4. 某班班主任为了了解该班学生寒假期间做家务劳动的情况，随机抽取该班15名学生，调查得到这15名学生寒假期间做家务劳动的天数分别是8，18，15，20，16，21，19，18，19，10，6，20，20，23，25，这组数据的中位数和众数分别是（    ）

A 18，20 B. 18.5，20 C. 19，20 D. 19.5，20

5. 数学与建筑的结合造就建筑艺术品，如吉林大学的校门是一抛物线形水泥建筑物，如图.若将该大学的校门轮廓（忽略水泥建筑的厚度）近似看成抛物线的一部分，且点在该抛物线上，则该抛物线的焦点坐标是（    ）

A  B. （0，－1） C.  D.

6. 新高考按照“3+1+2”的模式设置，其中“3”为语文、数学、外语3门必考科目，“1”由考生在物理、历史2门科目中选考1门科目，“2”由考生在化学、生物、政治、地理4门科目中选考2门科目，则学生甲选考的科目中包含物理和生物的概率是（    ）

A.  B.  C.  D.

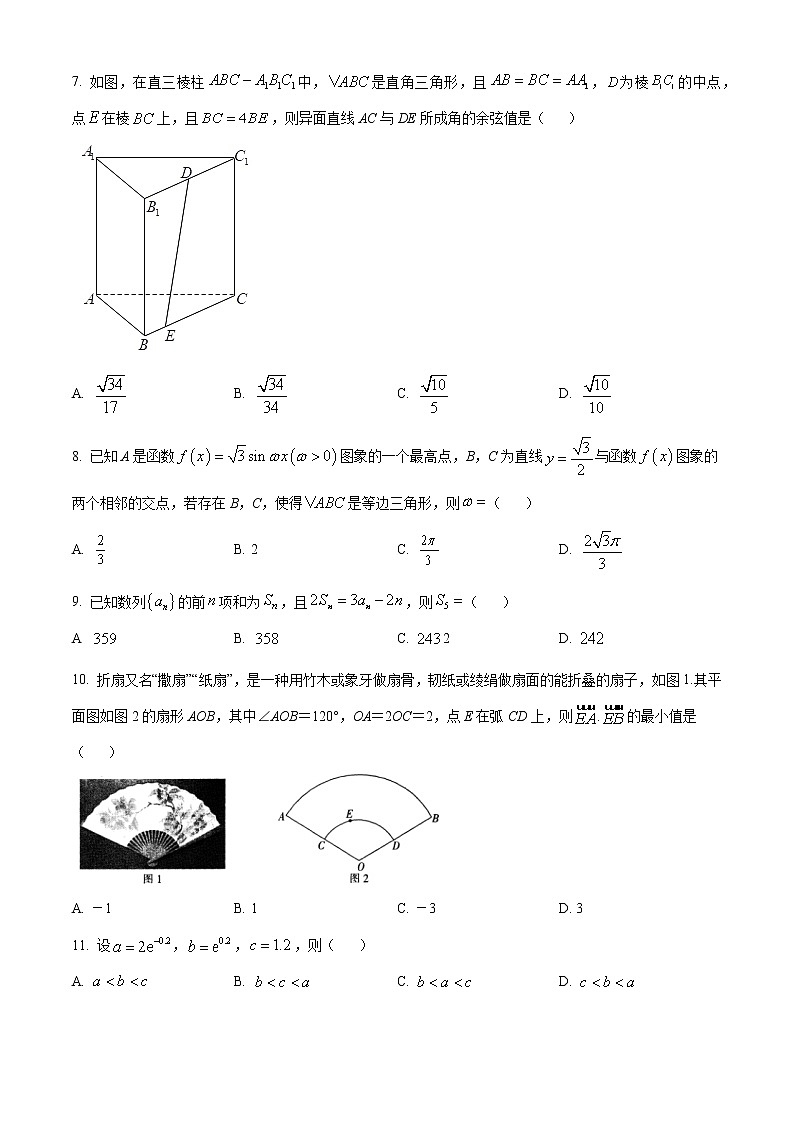
7. 如图，在直三棱柱中，是直角三角形，且，为棱的中点，点在棱上，且，则异面直线AC与DE所成角的余弦值是（    ）

A.  B.  C.  D.

8. 已知A是函数图象的一个最高点，B，C为直线与函数图象的两个相邻的交点，若存在B，C，使得是等边三角形，则（    ）

A.  B. 2 C.  D.

9. 已知数列的前项和为，且，则（    ）

A  B.  C. 2 D.

10. 折扇又名“撒扇”“纸扇”，是一种用竹木或象牙做扇骨，韧纸或绫绢做扇面的能折叠的扇子，如图1.其平面图如图2的扇形AOB，其中∠AOB＝120°，OA＝2OC＝2，点E在弧CD上，则的最小值是（    ）

A. －1 B. 1 C. －3 D. 3

11. 设，，，则（    ）

A.  B.  C.  D.

12. 已知双曲线E：的左焦点为F，过点F的直线l垂直于双曲线E的一条渐近线，垂足为M，直线l与双曲线E交于点N，且，则双曲线E的离心率为（    ）

A.  B.  C.  D.

二､填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.

13. 已知函数是定义在上的奇函数，则______.

14. 已知实数x，y满足约束条件，则的最大值为______．

15. 已知直线是曲线的切线，则______．

16. 数学中有许多形状优美、寓意独特几何体，“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的公共部分.如图，在勒洛四面体中，正四面体ABCD的棱长为4，则该勒洛四面体内切球的半径是______.

三､解答题：共70分.解答应写出必要的文字说明､证明过程或演算步骤.17~21题为必考题，每个试题考生都必须作答.第22，23题为选考题，考生根据要求作答.

17. 北京冬季奥运会的成功举办，引起了人们对冰雪运动的关注．某机构为了了解青少年对冰雪运动的喜爱情况，随机抽取了100名男青少年和100名女青少年，调查他们对冰雪运动的喜爱情况，得到下面的列联表：

（1）分别估计男、女青少年喜爱冰雪运动的概率；

（2）能否有95%的把握认为是否喜爱冰雪运动与性别有关？

参考公式：，其中．

参考数据：

18. 在△ABC中，内角A，B，C的对边分别为a，b，c，△ABC的面积.

（1）求角A值；

（2）延长AC至点D，使得CD＝AC，且BD＝2BC，若c＝6，求△ABC的周长.

19. 如图，四边形ABCD是圆柱的轴截面，，O分别是上、下底面圆的圆心，EF是底面圆的一条直径，．

（1）证明：．

（2）若，求三棱锥的体积．

20. 已知椭圆C：的左、右焦点分别为，，椭圆C的离心率小于.点P在椭圆C上，，且面积的最大值为.

（1）求椭圆C的标准方程；

（2）点M（1，1），A，B是椭圆C上不同的两点，点N在直线l：上，且，，试问是否为定值？若是，求出该定值；若不是，请说明理由.

21. 已知函数．

（1）试比较与的大小．

（2）证明：，．

22. 在平面直角坐标系xOy中，曲线C的参数方程为（为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程是.

（1）求曲线C的普通方程和直线l的直角坐标方程；

（2）已知P，Q分别是曲线C和直线l上的动点，求的最小值.

23. 已知函数.

（1）当a＝1时，求不等式的解集；

（2）若关于x的不等式恒成立，求a的取值范围.

2021-2022年昌吉学联体第三次高三年级高考适应性考试

文科数学试卷

一､选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

【1题答案】

【答案】A

【2题答案】

【答案】C

【3题答案】

【答案】B

【4题答案】

【答案】C

【5题答案】

【答案】A

【6题答案】

【答案】B

【7题答案】

【答案】B

【8题答案】

【答案】C

【9题答案】

【答案】B

【10题答案】

【答案】C

【11题答案】

【答案】D

【12题答案】

【答案】C

二､填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.

【13题答案】

【答案】

【14题答案】

【答案】11

【15题答案】

【答案】

【16题答案】

【答案】

三､解答题：共70分.解答应写出必要的文字说明､证明过程或演算步骤.17~21题为必考题，每个试题考生都必须作答.第22，23题为选考题，考生根据要求作答.

【17~18题答案】

【答案】（1）；.   

（2）有95%的把握认为是否喜爱冰雪运动与性别有关

【19~20题答案】

【答案】（1）；   

（2）

【21~22题答案】

【答案】（1）证明见解析   

（2）

【23~24题答案】

【答案】（1）   

（2）是定值，定值为

【25~26题答案】

【答案】（1），理由见解析；   

（2）证明见解析

【27~28题答案】

【答案】（1）曲线C的普通方程为，直线l的直角坐标方程为   

（2）

【29~30题答案】

【答案】（1）   

（2）