

山东省邹城市2022年初中学业水平模拟检测(一模)数学试题
展开2022年初中学业水平模拟检测(一)
数 学 试 题
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)
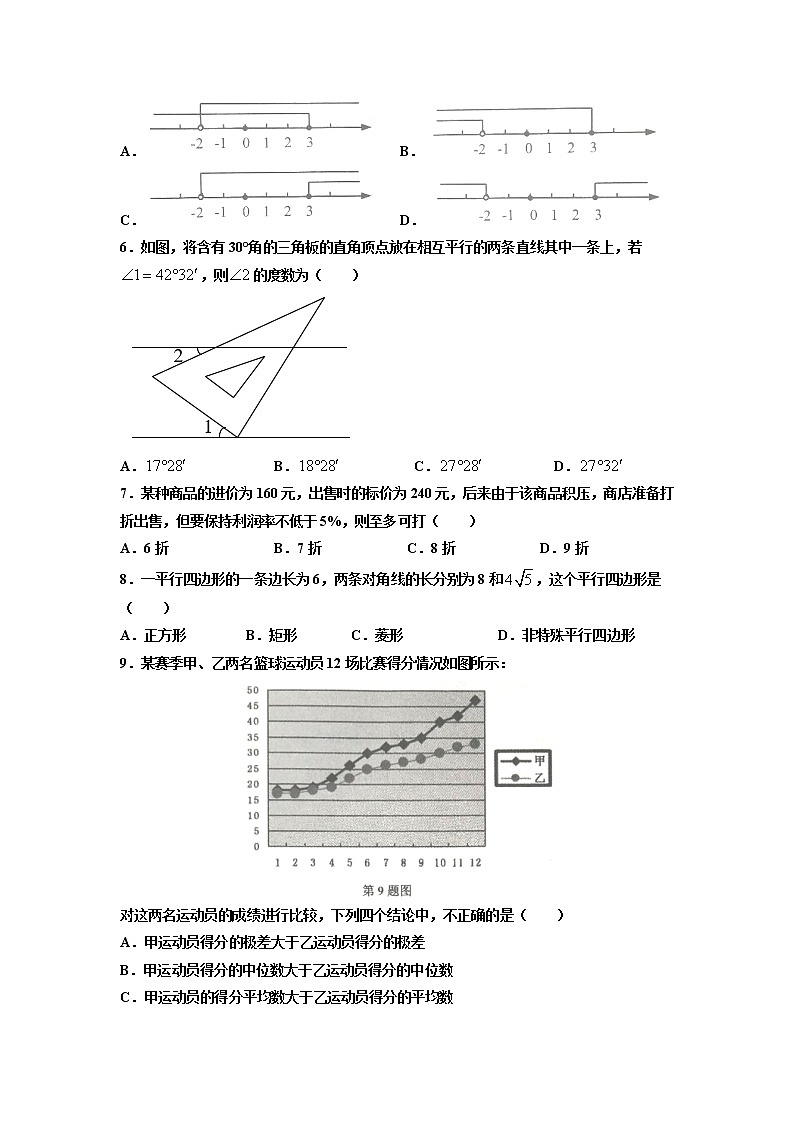
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.正五边形 D.圆
2.下列等式成立的是( )
A. B.
C. D.
3.蜜蜂建造的蜂巢既坚固又省料,其厚度约为0.000073米,将0.000073用科学记数法表示为( )
A. B. C. D.
4.如图是由六个相同的小正方体组成的立体图形,它的俯视图是( )
A. B.
C. D.
5.不等式组的解在数轴上表示正确的是( )
A. B.
C. D.
6.如图,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若,则的度数为( )
A. B. C. D.
7.某种商品的进价为160元,出售时的标价为240元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )
A.6折 B.7折 C.8折 D.9折
8.一平行四边形的一条边长为6,两条对角线的长分别为8和,这个平行四边形是( )
A.正方形 B.矩形 C.菱形 D.非特殊平行四边形
9.某赛季甲、乙两名篮球运动员12场比赛得分情况如图所示:
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员的得分平均数大于乙运动员得分的平均数
D.甲运动员的成绩比乙运动员的成绩稳定
10.如图所示,边长分别为1和2的两个正方形,其一边在同水平线上,小正方形沿该水平线自左向右匀速运动穿过大正方形,设运动时间为t,大正方形内除去小正方形部分的面积为S(阴影部分),那么S与t的大致图象应为( )
A. B.
C. D.
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.在函数中,自变量x的取值范围是__________.
12.若点和点关于y轴对称,则点在第__________象限.
13.某校研究性学习小组测量学校旗杆的高度,如图,在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆的高度为__________米.
14.小明从家步行到学校需走的路程为1800米,图中的折线反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行__________米.
15.如图,E,F分别为矩形的边,上的点,将矩形沿,所在直线折叠,点A和点C分别落在上的点M处和点N处,连接.已知,,则的长为__________.
三、解答题(本大题共7个小题,共55分)
16.(本题满分6分)
先化简再求值:,其中a满足.
17.(本题满分7分)
小明在“统计”实习活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图1;
(2)求图2中表示家长“无所谓”圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
18.(本题满分7分)
如图,四边形内接于,且为直径,,过A点的的垂线交的延长线于点E.
(1)求证:;
(2)如果,求图中阴影的面积.
19.(本题满分7分)
如图,在平面直角坐标系中,直线与y轴相交于点A,与反比例函数在第一象限内的图象相交于点.
(1)求反比例函数的解析式;
(2)将直线向上平移后与反比例函数的图象在第一象限内交于点C,且的面积为18,求平移后直线的解析式.
20.(本题满分9分)
如图,是的高,是的中线,,,,直线交于点M,交于点N.
(1)求证:四边形是平行四边形;
(2)求的度数;
(3)当,时,求线段的长.
21.(本题满分9分)
某公司为一工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
22.(本题满分10分)
如图,已知二次函数的图象交x轴分别于A,D两点,交y轴于B点,顶点为C.
(1)求抛物线的对称轴;
(2)求;
(3)在y轴上是否存在一点P,使得以P,B,D三点为顶点的三角形与相似?如果存在,请求出点P的坐标:如果不存在,请说明理由。
九年级数学试题参考答案
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | C | B | B | A | A | B | C | D | A |
二、填空题
11.x≥2; 12.四; 13. 9; 14. 350; 15.;
三、解答题
16.化简结果:(a+1)(a-2) ; 求值结果:-2
17.(1)家长总数200÷50%=400名;
表示“无所谓”人数:400-200-16-400×26%=80名
画图(略)
(2)(80÷400)×360°=72°
(3)
18.(1)证明过程略(2)阴影面积为
19.(1)反比例解析式为
(2)提示:设C点的坐标为(m,n),∵△ABC的面积为18
∴ ∴n-m=7
又C点在上,∴mn=8 ∴m=1,n=8
设平移后的直线解析式为y=x+b,代入(1,8)得平移后直线解析式为y=x+7
20.(1)提示:证△ACD≌△DEB可得CD=BE
(2)MH=1
提示:设MH=x,则CH=x ∴BH=x
由(1)知,CE∥AB,∴ ∴
解得x=1
21.略解:
(1)(吨)
(2),化简得:
(3)
经销店要获得最大月利润,材料的售价应定为每吨210元。
22.(1)x=1
(2)提示:求得:A(3,0),B(0,3),C(1,4),D(-1,0)
过点C作CE⊥y轴,垂足为E
∵△AOB和△BCE都是等腰直角三角形,
∴∠ABC=90°且
∴tan∠BAC=
(3)提示:在y轴上存在一点P,使得△PBD与△ABC相似
①P在原点时,∵PD=1,BP=3,∠BPD=∠ABC=90°
且,∴△BPD∽△ABC. 此时,P为(0,0)
②当P在y轴负半轴时,设P为(0,a),由①知∠DBP=∠BAC
∴只需∠BDP=90°即可. 此时,易证△BDO∽△DOP,∴
∴. 此时,P为(0,)
③当P在y轴正半轴时,显然△BDP不是直角三角形
∴所以满足题意的P点为(0,0)或(0,)
贵州省遵义市2023年初中学业水平考试模拟数学试题(一模): 这是一份贵州省遵义市2023年初中学业水平考试模拟数学试题(一模),共6页。
2023年山东省滕州市九年级初中学业水平考试模拟(一模)数学试题(含答案): 这是一份2023年山东省滕州市九年级初中学业水平考试模拟(一模)数学试题(含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山东省邹城市2022年初中学业水平模拟检测(一模)数学试题(word版含答案): 这是一份山东省邹城市2022年初中学业水平模拟检测(一模)数学试题(word版含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












