山东省烟台市2022年九年级数学中考复习《填空题常考热点》中档题专题提升训练

这是一份山东省烟台市2022年九年级数学中考复习《填空题常考热点》中档题专题提升训练，共13页。试卷主要包含了已知2＝　 　等内容，欢迎下载使用。
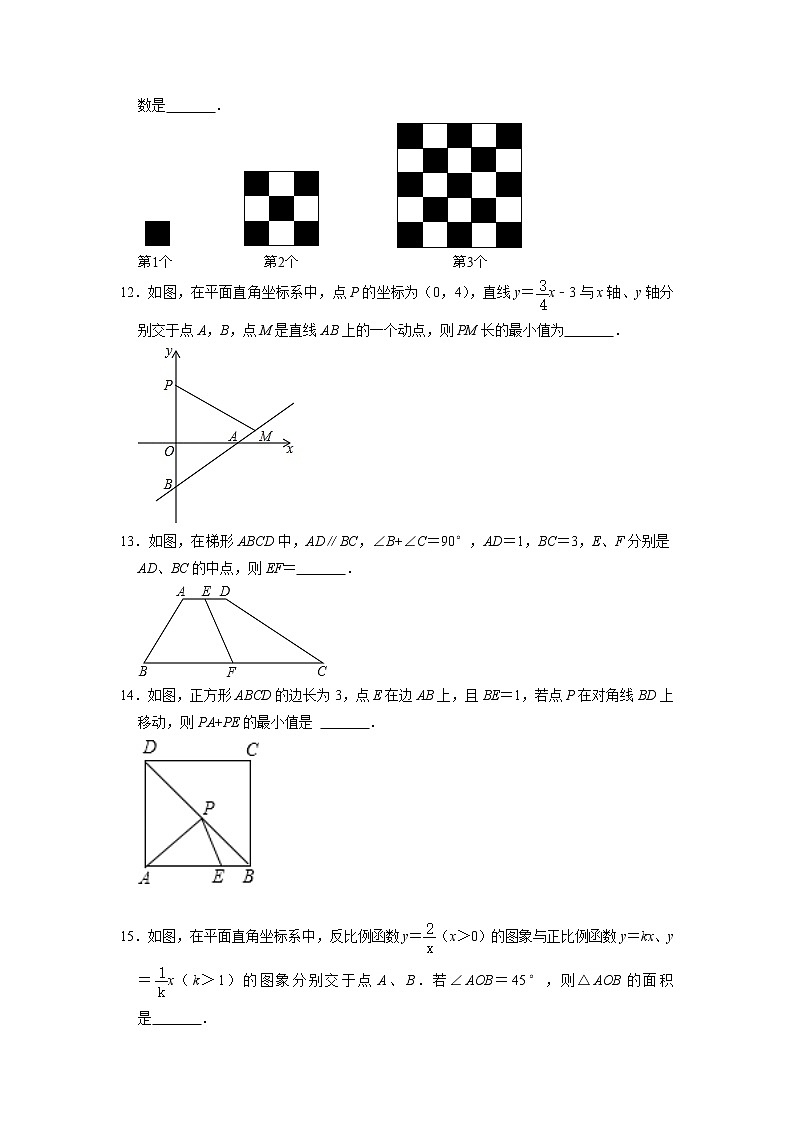
山东省烟台市2022年春九年级数学中考复习《填空题常考热点》中档题专题提升训练（附答案）1．若正实数m，n满足等式（m+n﹣1）2＝（m﹣1）2+（n﹣1）2，则m•n＝　   　．2．已知（a+1）（a+2）＝3，则（a+1）2+（a+2）2＝　   　．3．直角三角形的两条直角边分别是5和12，则它的内切圆半径为　   　．4．如图，∠MAN＝60°，若△ABC的顶点B在射线AM上，且AB＝2，点C在射线AN上运动，当△ABC是锐角三角形时，BC的取值范围是　   　．5．若关于x的分式方程＝﹣3有增根，则实数m的值是 　   　．6．关于x的分式方程+＝1的解为正数，则a的取值范围是　   　．7．当x＝m和x＝n（m≠n）时，二次函数y＝x2﹣2x+3的函数值相等，当x＝m+n时，函数y＝x2﹣2x+3的值为　   　．8．如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1　   　S2．（填“＞”“＝”或“＜”）9．如图，在矩形ABCD中，AD＝4，点P是直线AD上一动点，若满足△PBC是等腰三角形的点P有且只有3个，则AB的长为　   　．10．在平面直角坐标系xOy中，一次函数与反比例函数的图象交点的横坐标为x0．若k＜x0＜k+1，则整数k的值是　   　．11．按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的块数是　   　．12．如图，在平面直角坐标系中，点P的坐标为（0，4），直线y＝x﹣3与x轴、y轴分别交于点A，B，点M是直线AB上的一个动点，则PM长的最小值为　   　．13．如图，在梯形ABCD中，AD∥BC，∠B+∠C＝90°，AD＝1，BC＝3，E、F分别是AD、BC的中点，则EF＝　   　．14．如图，正方形ABCD的边长为3，点E在边AB上，且BE＝1，若点P在对角线BD上移动，则PA+PE的最小值是 　   　． 15．如图，在平面直角坐标系中，反比例函数y＝（x＞0）的图象与正比例函数y＝kx、y＝x（k＞1）的图象分别交于点A、B．若∠AOB＝45°，则△AOB的面积是　   　．16．如图，点A在反比例函数y＝（x＞0）的图象上，点B在x轴负半轴上，直线AB交y轴于点C，若＝，△AOB的面积为6，则k的值为　   　．17．如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，边AB、AC分别交⊙O于D、E两点，点B是的中点，则∠ABE＝　   　．18．如图，已知AB是半圆O的直径，AB＝6，点C，D在半圆上，OC⊥AB，＝2，点P是OC上的一个动点，则BP+DP的最小值为　   　． 19．《九章算术》中一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AC生长在它的中央，高出水面部分BC为1尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部C恰好碰到岸边的C'处（如图），水深和芦苇长各多少尺？则该问题的水深是 　   　尺．20．如图，点A是抛物线y＝x2上不与原点O重合的动点，AB⊥x轴于点B，过点B作OA的垂线并延长交y轴于点C，连结AC，则线段OC的长是 　   　，AC的最小值是 　   　．           参考答案1．解：∵（m+n﹣1）2＝（m﹣1）2+（n﹣1）2，∴m2+n2+1+2mn﹣2m﹣2n＝m2﹣2m+1+n2﹣2n+1，∴2mn＝1，∴mn＝，故答案为：．2．解：∵（a+1）（a+2）＝3，∴a2+3a+2＝3，∴a2+3a＝1∴（a+1）2+（a+2）2＝[（a+1）+（a+2）]2﹣2（a+1）（a+2）＝（2a+3）2﹣2×3＝4a2+12a+9﹣6＝4（a2+3a）+3＝4×1+3＝7故答案是：7．3．解：直角三角形的斜边＝＝13，所以它的内切圆半径＝＝2．故答案为2．4．解：如图，过点B作BC1⊥AN，垂足为C1，BC2⊥AM，交AN于点C2在Rt△ABC1中，AB＝2，∠A＝60°，∴∠ABC1＝30°∴AC1＝AB＝1，由勾股定理得：BC1＝，在Rt△ABC2中，AB＝2，∠A＝60°∴∠AC2B＝30°∴AC2＝4，由勾股定理得：BC2＝2，当△ABC是锐角三角形时，点C在C1C2上移动，此时＜BC＜2．故答案为：＜BC＜2．5．解：去分母，得：m＝x﹣1﹣3（x﹣2），由分式方程有增根，得到x﹣2＝0，即x＝2，把x＝2代入整式方程可得：m＝1，故答案为：1．6．解：去分母得：1﹣a+2＝x﹣2，解得：x＝5﹣a，5﹣a＞0，解得：a＜5，∵x≠2，∴a≠3，故a＜5且a≠3．故答案为：a＜5且a≠3．7．解：∵当x＝m和x＝n（m≠n）时，二次函数y＝x2﹣2x+3＝（x﹣1）2+2的函数值相等，∴以m、n为横坐标的点关于直线x＝1对称，则＝1，∴m+n＝2，∵x＝m+n，∴x＝2，函数y＝4﹣4+3＝3．故答案为3．8．解：∵P是线段AB的黄金分割点，且PA＞PB，∴PA2＝PB•AB，又∵S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，∴S1＝PA2，S2＝PB•AB，∴S1＝S2．故答案为：＝．9．解：①如图，当AB＝AD时满足△PBC是等腰三角形的点P有且只有3个，△P1BC，△P2BC是等腰直角三角形，△P3BC是等腰直角三角形（P3B＝P3C），则AB＝AD＝4．②当AB＜AD，且满足△PBC是等腰三角形的点P有且只有3个时，如图，易知P2是AD的中点，∵△P1BC是等腰三角形，∴BP1＝BC，同理：BC＝CP3，只有△P2BC是等边三角形时，△PBC是等腰三角形的点P有且只有3个，∴BC＝BP1＝BP2＝CP2＝CP3∴BP2＝＝，又∵BP1＝BC，∴＝4∴AB＝2．③当AB＞AD时，直线AD上只有一个点P满足△PBC是等腰三角形．故答案为：4或2．10．解：联立两函数解析式得：，消去y得：x+2＝，即x2+6x＝15，配方得：x2+6x+9＝24，即（x+3）2＝24，解得：x＝2﹣3或﹣2﹣3（舍去），∴一次函数与反比例函数图象交点的横坐标为x0＝2﹣3，即k＜2﹣3＜k+1，则整数k＝1．故答案为：111．解：第1个图案只有1块黑色地砖，第2个图案有黑色与白色地砖共32＝9，其中黑色的有5块，第3个图案有黑色与白色地砖共52＝25，其中黑色的有13块，…第n个图案有黑色与白色地砖共（2n﹣1）2，其中黑色的有[（2n﹣1）2+1]，当n＝14时，黑色地砖的块数有[（2×14﹣1）2+1]＝×730＝365．故答案为：365．12．解：如图，过点P作PM⊥AB，则：∠PMB＝90°，     当PM⊥AB时，PM最短，因为直线y＝x﹣3与x轴、y轴分别交于点A，B，可得点A的坐标为（4，0），点B的坐标为（0，﹣3），在Rt△AOB中，AO＝4，BO＝3，AB＝＝5，∵∠BMP＝∠AOB＝90°，∠B＝∠B，PB＝OP+OB＝7，∴△PBM∽△ABO，∴＝，即：，所以可得：PM＝．13．解：过点E作AB、CD的平行线，与BC分别交于G，H，∵∠B+∠C＝90°，∴∠EGH＝∠B，∠EHG＝∠C，∴∠EGH+∠EHG＝90°，∴四边形ABGE和四边形CDEH都是平行四边形，△EGH为直角三角形，∵E、F分别是AD、BC的中点，∴BG＝CH＝0.5，GH＝2，根据直角三角形中斜边上的中线是斜边的一半知，EF＝GH＝1，∴EF＝1．14．解：作出点E关于BD的对称点E′交BC于E′，连接AE′与BD交于点P，此时AP+PE最小，∵PE＝PE′，∴AP+PE＝AP+PE′＝AE′，在Rt△ABE′中，AB＝3，BE′＝BE＝1，根据勾股定理得：AE′＝，则PA+PE的最小值为．故答案为：．15．解：如图，过B作BD⊥x轴于点D，过A作AC⊥y轴于点C设点A横坐标为a，则A（a，）∵A在正比例函数y＝kx图象上∴＝ka∴k＝同理，设点B横坐标为b，则B（b，）∴＝∴∴∴ab＝2当点A坐标为（a，）时，点B坐标为（，a）∴OC＝OD将△AOC绕点O顺时针旋转90°，得到△ODA′∵BD⊥x轴∴B、D、A′共线∵∠AOB＝45°，∠AOA′＝90°∴∠BOA′＝45°∵OA＝OA′，OB＝OB∴△AOB≌△A′OB∵S△BOD＝S△AOC＝2×＝1∴S△AOB＝2故答案为：216．解：过点A作AD⊥y轴于D，则△ADC∽△BOC，∴，∵＝，△AOB的面积为6，∴＝2，∴＝1，∴△AOD的面积＝3，根据反比例函数k的几何意义得，，∴|k|＝6，∵k＞0，∴k＝6．故答案为：6．17．解：如图，连接DC，∵∠DBC＝90°，∴DC是⊙O的直径，∵点B是的中点，∴∠BCD＝∠BDC＝45°，在Rt△ABC中，∠ABC＝90°，∠A＝32°，∴∠ACB＝90°﹣32°＝58°，∴∠ACD＝∠ACB﹣∠BCD＝58°﹣45°＝13°＝∠ABE，故答案为：13°．18．解：如图，连接AD，PA，PD，OD．∵OC⊥AB，OA＝OB，∴PA＝PB，∠COB＝90°，∵＝2，∴∠DOB＝×90°＝60°，∵OD＝OB，∴△OBD是等边三角形，∴∠ABD＝60°∵AB是直径，∴∠ADB＝90°，∴AD＝AB•sin∠ABD＝3，∵PB+PD＝PA+PD≥AD，∴PD+PB≥3，∴PD+PB的最小值为3，故答案为：3．19．解：依题意画出图形，设芦苇长AC＝AC′＝x尺，则水深AB＝（x﹣1）尺，∵C′E＝10尺，∴C′B＝5尺，在Rt△AC′B中，52+（x﹣1）2＝x2，解得x＝13，即芦苇长13尺，水深为12尺，故答案为：12．20．解：设点A（a，a2），则点B坐标为（a，0），∴OB＝|a|，AB＝a2，∵∠AOB+∠OBC＝90°，∠OBC+∠BCO＝90°，∴∠AOB＝∠BCO，∴△AOB∽△BCO，∴，∴OB2＝CO•AB，即a2＝a2•CO，解得CO＝8，∴C（0，8），∵AC2＝（xc﹣xA）2+（yC﹣yA）2＝a2+a4﹣2a2+64＝（a4﹣64a2）+64＝（a2﹣32）2+48，∴当a2＝32时，AC2＝48为最小值，即AC＝4．故答案为：8，4．