2022届浙江省台州市温岭市实验校中考适应性考试数学试题含解析

这是一份2022届浙江省台州市温岭市实验校中考适应性考试数学试题含解析，共23页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．已知，如图，AB是⊙O的直径，点D，C在⊙O上，连接AD、BD、DC、AC，如果∠BAD＝25°，那么∠C的度数是（　　）

A．75° B．65° C．60° D．50°
2．如图，空心圆柱体的左视图是（ ）

A． B． C． D．
3．如图，若a∥b，∠1=60°，则∠2的度数为（　　）

A．40° B．60° C．120° D．150°
4．实数a，b在数轴上对应的点的位置如图所示，则正确的结论是（　　）

A．a+b＜0 B．a＞|﹣2| C．b＞π D．
5．下面几何的主视图是（ ）

A． B． C． D．
6．△ABC在正方形网格中的位置如图所示，则cosB的值为( )

A． B． C． D．2
7．已知一元二次方程1–（x–3）（x+2）=0，有两个实数根x1和x2（x1 A．–2 8．如图，这是根据某班40名同学一周的体育锻炼情况绘制的条形统计图，根据统计图提供的信息，可得到该班40名同学一周参加体育锻炼时间的众数、中位数分别是（ ）

A．8，9 B．8，8.5 C．16，8.5 D．16，10.5
9．如果将抛物线向右平移1个单位，那么所得的抛物线的表达式是　　
A． B． C． D．
10．某厂进行技术创新，现在每天比原来多生产30台机器，并且现在生产500台机器所需时间与原来生产350台机器所需时间相同．设现在每天生产x台机器，根据题意可得方程为（　　）
A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．若3，a，4，5的众数是4，则这组数据的平均数是_____．
12．若关于的不等式组无解， 则的取值范围是 ________.
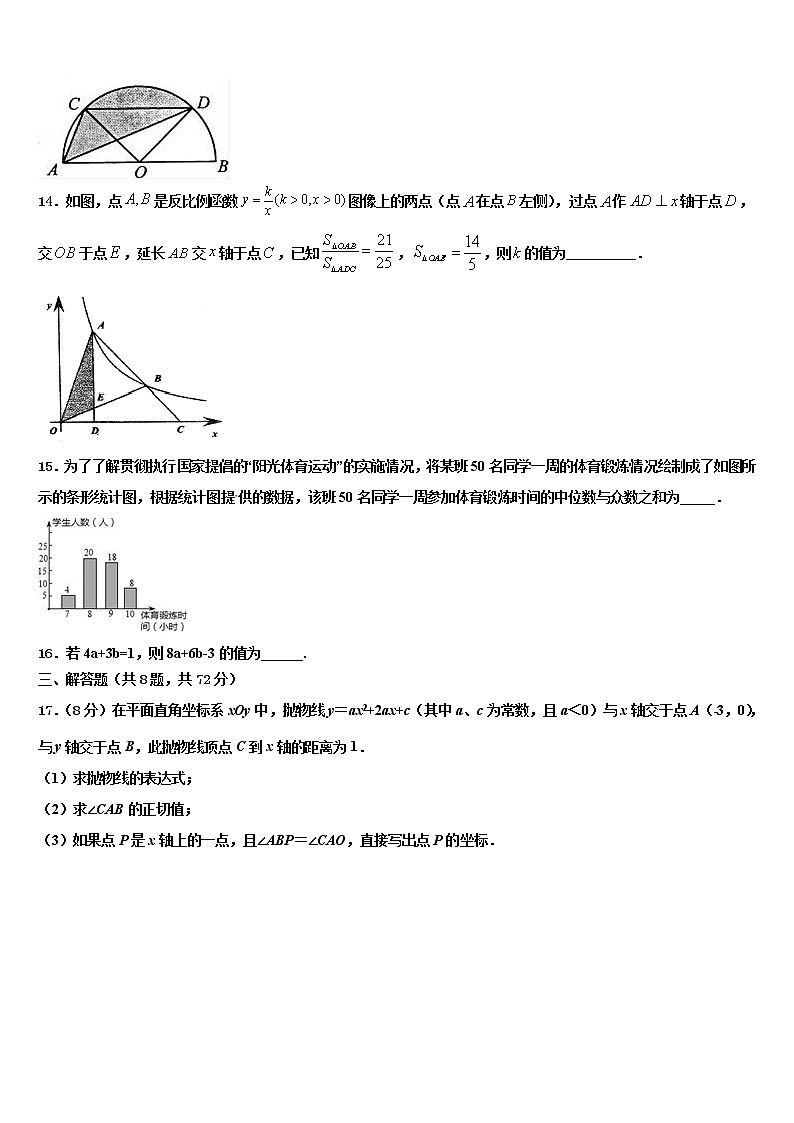
13．如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为_____．

14．如图，点是反比例函数图像上的两点（点在点左侧），过点作轴于点，交于点，延长交轴于点，已知，，则的值为__________．

15．为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况，将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图，根据统计图提供的数据，该班50名同学一周参加体育锻炼时间的中位数与众数之和为_____．

16．若4a+3b=1，则8a+6b-3的值为______.
三、解答题（共8题，共72分）
17．（8分）在平面直角坐标系xOy中，抛物线y＝ax2+2ax+c（其中a、c为常数，且a＜0）与x轴交于点A（﹣3，0），与y轴交于点B，此抛物线顶点C到x轴的距离为1．
（1）求抛物线的表达式；
（2）求∠CAB的正切值；
（3）如果点P是x轴上的一点，且∠ABP＝∠CAO，直接写出点P的坐标．

18．（8分）阅读
（1）阅读理解：

如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是________；
（2）问题解决：
如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．
19．（8分）如图,已知△ABC,以A为圆心AB为半径作圆交AC于E,延长BA交圆A于D连DE并延长交BC于F,
(1)判断△ABC的形状，并证明你的结论；
(2)如图1,若BE=CE=,求⊙A的面积；
(3)如图2,若tan∠CEF=,求cos∠C的值.

20．（8分）如图有A、B两个大小均匀的转盘，其中A转盘被分成3等份，B转盘被分成4等份，并在每一份内标上数字．小明和小红同时各转动其中一个转盘，转盘停止后（当指针指在边界线时视为无效，重转），若将A转盘指针指向的数字记作一次函数表达式中的k，将B转盘指针指向的数字记作一次函数表达式中的b．请用列表或画树状图的方法写出所有的可能；求一次函数y=kx+b的图象经过一、二、四象限的概率．

21．（8分）如图，AB为⊙O的直径，点E在⊙O上，C为的中点，过点C作直线CD⊥AE于D，连接AC、BC．
（1）试判断直线CD与⊙O的位置关系，并说明理由；
（2）若AD=2，AC=，求AB的长．

22．（10分）某商店经营儿童益智玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元．设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元．求y与x的函数关系式并直接写出自变量x的取值范围．每件玩具的售价定为多少元时，月销售利润恰为2520元？每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
23．（12分） “校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：

（1）接受问卷调查的学生共有　 　人，扇形统计图中“基本了解”部分所对应扇形的圆心角为　 　度；
（2）请补全条形统计图；
（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数．
24．如图，在Rt△ABC中，∠C=90°，O为BC边上一点，以OC为半径的圆O，交AB于D点，且AD=AC，延长DO交圆O于E点，连接AE.求证：DE⊥AB；若DB=4，BC=8，求AE的长.




参考答案

一、选择题（共10小题，每小题3分，共30分）
1、B
【解析】
因为AB是⊙O的直径，所以求得∠ADB=90°，进而求得∠B的度数，又因为∠B=∠C，所以∠C的度数可求出．
解：∵AB是⊙O的直径，
∴∠ADB=90°．
∵∠BAD=25°，
∴∠B=65°，
∴∠C=∠B=65°（同弧所对的圆周角相等）．
故选B．

2、C
【解析】
根据从左边看得到的图形是左视图，可得答案．
【详解】
从左边看是三个矩形，中间矩形的左右两边是虚线，
故选C．
【点睛】
本题考查了简单几何体的三视图，从左边看得到的图形是左视图．
3、C
【解析】
如图：

∵∠1=60°，
∴∠3=∠1=60°，
又∵a∥b，
∴∠2+∠3=180°，
∴∠2=120°，
故选C.
点睛：本题考查了平行线的性质，对顶角相等的性质，熟记性质是解题的关键.平行线的性质定理：两直线平行，同位角相等，内错角相等，同旁内角互补，两条平行线之间的距离处处相等.
4、D
【解析】
根据数轴上点的位置，可得a，b，根据有理数的运算，可得答案．
【详解】
a＝﹣2，2＜b＜1．
A.a+b＜0，故A不符合题意；
B.a＜|﹣2|，故B不符合题意；
C.b＜1＜π，故C不符合题意；
D.＜0，故D符合题意；
故选D．
【点睛】
本题考查了实数与数轴，利用有理数的运算是解题关键．
5、B
【解析】
主视图是从物体正面看所得到的图形．
【详解】
解：从几何体正面看
故选B．
【点睛】
本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
6、A
【解析】
解：在直角△ABD中，BD=2，AD=4，则AB=，
则cosB=．
故选A．

7、B
【解析】
设y=-（x﹣3）（x+2），y1=1﹣（x﹣3）（x+2）根据二次函数的图像性质可知y1=1﹣（x﹣3）（x+2）的图像可看做y=-（x﹣3）（x+2）的图像向上平移1个单位长度，根据图像的开口方向即可得出答案.
【详解】
设y=-（x﹣3）（x+2），y1=1﹣（x﹣3）（x+2）
∵y=0时，x=-2或x=3，
∴y=-（x﹣3）（x+2）的图像与x轴的交点为（-2，0）（3，0），
∵1﹣（x﹣3）（x+2）=0，
∴y1=1﹣（x﹣3）（x+2）的图像可看做y=-（x﹣3）（x+2）的图像向上平移1，与x轴的交点的横坐标为x1、x2，
∵-1<0，
∴两个抛物线的开口向下，
∴x1＜﹣2＜3＜x2，
故选B.
【点睛】
本题考查二次函数图像性质及平移的特点，根据开口方向确定函数的增减性是解题关键.
8、A
【解析】
根据中位数、众数的概念分别求得这组数据的中位数、众数．
【详解】
解：众数是一组数据中出现次数最多的数，即8；
而将这组数据从小到大的顺序排列后，处于20，21两个数的平均数，由中位数的定义可知，这组数据的中位数是9.
故选A．
【点睛】
考查了中位数、众数的概念．本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(最中间两个数的平均数)，叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．
9、D
【解析】
本题主要考查二次函数的解析式
【详解】
解：根据二次函数的解析式形式可得，设顶点坐标为(h,k)，则二次函数的解析式为.由原抛物线解析式可得a=1，且原抛物线的顶点坐标为(0,0)，向右平移1个单位后的顶点坐标为(1,0)，故平移后的解析式为.
故选D.
【点睛】
本题主要考查二次函数的顶点式，根据顶点的平移可得到二次函数平移后的解析式.
10、A
【解析】
根据现在生产500台机器所需时间与原计划生产350台机器所需时间相同，所以可得等量关系为：现在生产500台机器所需时间=原计划生产350台机器所需时间．
【详解】
现在每天生产x台机器，则原计划每天生产（x﹣30）台机器．
依题意得：，
故选A．
【点睛】
本题考查了分式方程的应用，弄清题意，找准等量关系列出方程是解题的关键.

二、填空题（本大题共6个小题，每小题3分，共18分）
11、4
【解析】
试题分析：先根据众数的定义求出a的值，再根据平均数的定义列出算式，再进行计算即可．
试题解析：∵3，a，4，5的众数是4，
∴a=4，
∴这组数据的平均数是（3+4+4+5）÷4=4.
考点：1.算术平均数；2.众数．
12、
【解析】
首先解每个不等式，然后根据不等式无解，即两个不等式的解集没有公共解即可求得．
【详解】
，
解①得：x＞a+3，
解②得：x＜1．
根据题意得：a+3≥1，
解得：a≥-2．
故答案是：a≥-2．
【点睛】
本题考查了一元一次不等式组的解，解题的关键是熟练掌握解一元一次不等式组的步骤.．
13、
【解析】
解：∵弦CD∥AB，∴S△ACD=S△OCD，∴S阴影=S扇形COD==．故答案为．
14、
【解析】
过点B作BF⊥OC于点F，易证S△OAE=S四边形DEBF=，S△OAB=S四边形DABF，因为，所以，，又因为AD∥BF，所以S△BCF∽S△ACD，可得BF:AD=2：5，因为S△OAD=S△OBF，所以×OD×AD =×OF×BF，即BF:AD=2：5= OD：OF，易证：S△OED∽S△OBF，S△OED：S△OBF=4:25，S△OED：S四边形EDFB=4:21，所以S△OED= ，S△OBF= S△OED+ S四边形EDFB=+=, 即可得解：k=2 S△OBF=.
【详解】
解：过点B作BF⊥OC于点F，

由反比例函数的比例系数|k|的意义可知：S△OAD=S△OBF，
∴S△OAD- S△OED =S△OBF一S△OED，即S△OAE=S四边形DEBF=，S△OA B=S四边形DABF，
∵，
∴，，
∵AD∥BF
∴S△BCF∽S△ACD，
又∵，
∴BF:AD=2：5，
∵S△OAD=S△OBF，
∴×OD×AD =×OF×BF
∴BF:AD=2：5= OD：OF
易证：S△OED∽S△OBF，
∴S△OED：S△OBF=4:25，S△OED：S四边形EDFB=4:21
∵S四边形EDFB=，
∴S△OED= ，S△OBF= S△OED+ S四边形EDFB=+=,
∴k=2 S△OBF=.
故答案为.
【点睛】
本题考查反比例函数的比例系数|k|的几何意义，解题关键是熟练运用相似三角形的判定定理和性质定理.
15、17
【解析】
∵8是出现次数最多的，∴众数是8，
∵这组数据从小到大的顺序排列，处于中间位置的两个数都是9，∴中位数是9，
所以中位数与众数之和为8+9=17.
故答案为17小时.
16、-1
【解析】
先求出8a+6b的值，然后整体代入进行计算即可得解．
【详解】
∵4a+3b=1，
∴8a+6b=2，
8a+6b-3=2-3=-1；
故答案为：-1．
【点睛】
本题考查了代数式求值，整体思想的利用是解题的关键．

三、解答题（共8题，共72分）
17、（4）y＝﹣x4﹣4x+3；（4）；（3）点P的坐标是（4，0）
【解析】
(4) 先求得抛物线的对称轴方程, 然后再求得点C的坐标,设抛物线的解析式为y＝a（x+4）4+4,将点 (-3, 0) 代入求得a的值即可;
(4) 先求得A、 B、 C的坐标, 然后依据两点间的距离公式可得到BC、AB,AC的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;
(3) 连接BC,可证得△AOB是等腰直角三角形，△ACB∽△BPO，可得代入个数据可得OP的值，可得P点坐标.
【详解】
解：（4）由题意得，抛物线y＝ax4+4ax+c的对称轴是直线，
∵a＜0，抛物线开口向下，又与x轴有交点，
∴抛物线的顶点C在x轴的上方，
由于抛物线顶点C到x轴的距离为4，因此顶点C的坐标是（﹣4，4）．
可设此抛物线的表达式是y＝a（x+4）4+4，
由于此抛物线与x轴的交点A的坐标是（﹣3，0），可得a＝﹣4．
因此，抛物线的表达式是y＝﹣x4﹣4x+3．
（4）如图4，

点B的坐标是（0，3）．连接BC．
∵AB4＝34+34＝48，BC4＝44+44＝4，AC4＝44+44＝40，
得AB4+BC4＝AC4．
∴△ABC为直角三角形，∠ABC＝90°，
所以tan∠CAB=．
即∠CAB的正切值等于．
（3）如图4，连接BC，
∵OA＝OB＝3，∠AOB＝90°，
∴△AOB是等腰直角三角形，
∴∠BAP＝∠ABO＝45°，
∵∠CAO＝∠ABP，
∴∠CAB＝∠OBP，
∵∠ABC＝∠BOP＝90°，
∴△ACB∽△BPO，
∴，
∴，OP＝4，
∴点P的坐标是（4，0）．
【点睛】
本题主要考查二次函数的图像与性质，综合性大.
18、（1）2＜AD＜8；（2）证明见解析；（3）BE+DF=EF；理由见解析.
【解析】
试题分析：（1）延长AD至E，使DE=AD，由SAS证明△ACD≌△EBD，得出BE=AC=6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；
（2）延长FD至点M，使DM=DF，连接BM、EM，同（1）得△BMD≌△CFD，得出BM=CF，由线段垂直平分线的性质得出EM=EF，在△BME中，由三角形的三边关系得出BE+BM＞EM即可得出结论；
（3）延长AB至点N，使BN=DF，连接CN，证出∠NBC=∠D，由SAS证明△NBC≌△FDC，得出CN=CF，∠NCB=∠FCD，证出∠ECN=70°=∠ECF，再由SAS证明△NCE≌△FCE，得出EN=EF，即可得出结论．
试题解析：（1）解：延长AD至E，使DE=AD，连接BE，如图①所示：
∵AD是BC边上的中线，
∴BD=CD，
在△BDE和△CDA中，BD=CD，∠BDE=∠CDA，DE=AD，
∴△BDE≌△CDA（SAS），
∴BE=AC=6，
在△ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，
∴10﹣6＜AE＜10+6，即4＜AE＜16，
∴2＜AD＜8；
故答案为2＜AD＜8；
（2）证明：延长FD至点M，使DM=DF，连接BM、EM，如图②所示：
同（1）得：△BMD≌△CFD（SAS），
∴BM=CF，
∵DE⊥DF，DM=DF，
∴EM=EF，
在△BME中，由三角形的三边关系得：BE+BM＞EM，
∴BE+CF＞EF；
（3）解：BE+DF=EF；理由如下：
延长AB至点N，使BN=DF，连接CN，如图3所示：
∵∠ABC+∠D=180°，∠NBC+∠ABC=180°，
∴∠NBC=∠D，
在△NBC和△FDC中，
BN=DF，∠NBC =∠D，BC=DC，
∴△NBC≌△FDC（SAS），
∴CN=CF，∠NCB=∠FCD，
∵∠BCD=140°，∠ECF=70°，
∴∠BCE+∠FCD=70°，
∴∠ECN=70°=∠ECF，
在△NCE和△FCE中，
CN=CF，∠ECN=∠ECF，CE=CE，
∴△NCE≌△FCE（SAS），
∴EN=EF，
∵BE+BN=EN，
∴BE+DF=EF．

考点：全等三角形的判定和性质；三角形的三边关系定理.
19、 (1) △ABC为直角三角形，证明见解析；（2）12π；（3）.
【解析】
（1）由,得△CEF∽△CBE,∴∠CBE=∠CEF，由BD为直径,得∠ADE+∠ABE=90°,即可得∠DBC=90°故△ABC为直角三角形.(2)设∠EBC=∠ECB=x,根据等腰三角形的性质与直角三角形的性质易得 x=30°，则∠ABE=60°故AB=BE=，则可求出求⊙A的面积；(3)由(1)知∠D=∠CFE=∠CBE,故tan∠CBE=,设EF=a,BE=2a,利用勾股定理求出 BD=2BF=,得AD=AB=，DE=2BE=4a,过F作FK∥BD交CE于K,利用平行线分线段成比例得，求得 ， 即可求出tan∠C＝ 再求出cos∠C即可.
【详解】
解：∵,
∴,
∴△CEF∽△CBE,
∴∠CBE=∠CEF，
∵AE=AD,
∴∠ADE=∠AED=∠FEC=∠CBE,
∵BD为直径,
∴∠ADE+∠ABE=90°,
∴∠CBE+∠ABE=90°,
∴∠DBC=90°△ABC为直角三角形.
(2)∵BE=CE
∴设∠EBC=∠ECB=x,
∴∠BDE=∠EBC=x,
∵AE=AD
∴∠AED=∠ADE=x,
∴∠CEF=∠AED=x
∴∠BFE=2x
在△BDF中由△内角和可知:
3x=90°
∴x=30°
∴∠ABE=60°
∴AB=BE=
∴
(3)由(1)知:∠D=∠CFE=∠CBE,
∴tan∠CBE=,
设EF=a,BE=2a,
∴BF=,BD=2BF=,
∴AD=AB=，
∴,DE=2BE=4a,过F作FK∥BD交CE于K,
∴， 　
∵，　
∴
∴，
∴tan∠C＝
∴cos∠C＝.

【点睛】
此题主要考查圆内的三角形综合问题，解题的关键是熟知圆的切线定理，等腰三角形的性质，及相似三角形的性质.
20、（1）答案见解析；（2）．
【解析】
（1）k可能的取值为-1、-2、-3，b可能的取值为-1、-2、3、4，所以将所有等可能出现的情况用列表方式表示出来即可．
（2）判断出一次函数y=kx+b经过一、二、四象限时k、b的正负，在列表中找出满足条件的情况，利用概率的基本概念即可求出一次函数y=kx+b经过一、二、四象限的概率．
【详解】
解：（1）列表如下：

所有等可能的情况有12种；
（2）一次函数y=kx+b的图象经过一、二、四象限时，k＜0，b＞0，情况有4种，
则P== ．
21、（1）证明见解析（2）3
【解析】
（1）连接，由为的中点，得到，等量代换得到，根据平行线的性质得到，即可得到结论；
（2）连接，由勾股定理得到，根据切割线定理得到，根据勾股定理得到，由圆周角定理得到，即可得到结论.
【详解】
相切，连接，
∵为的中点，
∴，
∵，
∴，
∴，
∴，
∵，
∴，

∴直线与相切；
方法：连接，
∵，，
∵，
∴，
∵是的切线，
∴，
∴，
∴，
∵为的中点，
∴，
∵为的直径，
∴，
∴．
方法：∵，
易得，
∴，
∴．
【点睛】
本题考查了直线与圆的位置关系，切线的判定和性质，圆周角定理，勾股定理，平行线的性质，切割线定理，熟练掌握各定理是解题的关键.
22、（1）y＝﹣10x2+130x+2300，0＜x≤10且x为正整数；（2）每件玩具的售价定为32元时，月销售利润恰为2520元；（3）每件玩具的售价定为36元或37元时，每个月可获得最大利润，最大的月利润是2720元.
【解析】
（1）根据题意知一件玩具的利润为（30+x-20）元，月销售量为（230-10x），然后根据月销售利润=一件玩具的利润×月销售量即可求出函数关系式．
（2）把y=2520时代入y=-10x2+130x+2300中，求出x的值即可．
（3）把y=-10x2+130x+2300化成顶点式，求得当x=6.5时，y有最大值，再根据0＜x≤10且x为正整数，分别计算出当x=6和x=7时y的值即可．
【详解】
（1）根据题意得：
y＝（30+x﹣20）（230﹣10x）＝﹣10x2+130x+2300，
自变量x的取值范围是：0＜x≤10且x为正整数；
（2）当y＝2520时，得﹣10x2+130x+2300＝2520，
解得x1＝2，x2＝11（不合题意，舍去）
当x＝2时，30+x＝32（元）
答：每件玩具的售价定为32元时，月销售利润恰为2520元．
（3）根据题意得：
y＝﹣10x2+130x+2300
＝﹣10（x﹣6.5）2+2722.5，
∵a＝﹣10＜0，
∴当x＝6.5时，y有最大值为2722.5，
∵0＜x≤10且x为正整数，
∴当x＝6时，30+x＝36，y＝2720（元），
当x＝7时，30+x＝37，y＝2720（元），
答：每件玩具的售价定为36元或37元时，每个月可获得最大利润，最大的月利润是2720元．
【点睛】
本题主要考查了二次函数的实际应用，解题的关键是分析题意，找到关键描述语，求出函数的解析式，用到的知识点是二次函数的性质和解一元二次方程．
23、 (1) 60，90；(2)见解析;(3) 300人
【解析】
（1）由了解很少的有30人，占50%，可求得接受问卷调查的学生数，继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角；
（2）由（1）可求得了解的人数，继而补全条形统计图；
（3）利用样本估计总体的方法，即可求得答案．
【详解】
解：（1）∵了解很少的有30人，占50%，
∴接受问卷调查的学生共有：30÷50%=60（人）；
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为：×360°=90°；
故答案为60，90；
（2）60﹣15﹣30﹣10=5；
补全条形统计图得：

（3）根据题意得：900×=300（人），
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人．
【点睛】
本题考查了条形统计图与扇形统计图，解题的关键是熟练的掌握条形统计图与扇形统计图的相关知识点.
24、（1）详见解析；（2）6
【解析】
（1）连接CD，证明即可得到结论；
（2）设圆O的半径为r，在Rt△BDO中，运用勾股定理即可求出结论.
【详解】
（1）证明：连接CD,

∵
∴
∵
∴
.
（2）设圆O的半径为，，
设.
【点睛】
本题综合考查了切线的性质和判定及勾股定理的综合运用．综合性比较强，对于学生的能力要求比较高．