

2022年四川省泸州市泸县初第二次学业水平模拟考试数学试题
展开这是一份2022年四川省泸州市泸县初第二次学业水平模拟考试数学试题,共10页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
泸县初中2022届第二次学业水平模拟考试
数学试卷
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12个小题,每小题3分,共36分)在每小题给出的四个选项中,有且只有一个是正确的,清将正确选项的字母填涂在答题卡相应的位置上.
1.下列各数中,比-3小的数是( )
A.-2 B.-1 C.0 D.-4
2.面对2020年突如其来的新冠疫情,党和国家及时采取“严防严控”措施,并对新冠患者全部免费治疗.据统计共投入约2100000000元资金.2100000000用科学记数法可表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.某几何体的三视图如右图,该几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.三棱柱
5.点关于原点对称的对称点的坐标为( )
A. B. C. D.
6.如图,,,的角平分线EG交CD于点G,则的度数为( )
A.55° B.56° C.57° D.58°
7.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.这组数据的平均数与中位数分别为( )
A.11,12 B.11,11 C.12,11 D.13,11
8.如图,的直径AB=4,点C在上,.则BC的长是( )
A.2 B. C. D.
9.圆锥的底面半径为1,母线长为3,则该圆锥侧面积为( )
A.3 B. C. D.6
10.若一元二次方程有实数根,则的取值范围是( )
A. B.且 C. D.且
11.若关于x的分式方程的解为正数,则m的取值范围为( )
A. B. C.且 D.且
12.在平面直角坐标系中,将抛物线沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
第Ⅱ卷(非选择题 共84分)
二、填空题(每小题3分,共12分)
13.若式子在实数范围内有意义,则x的取值范围是______.
14.已知方程的两个根分别是,,则的值为______.
15.数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.如图,在菱形ABCD中,AB=2,,建立平面直角坐标系,使得边AB在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是______.
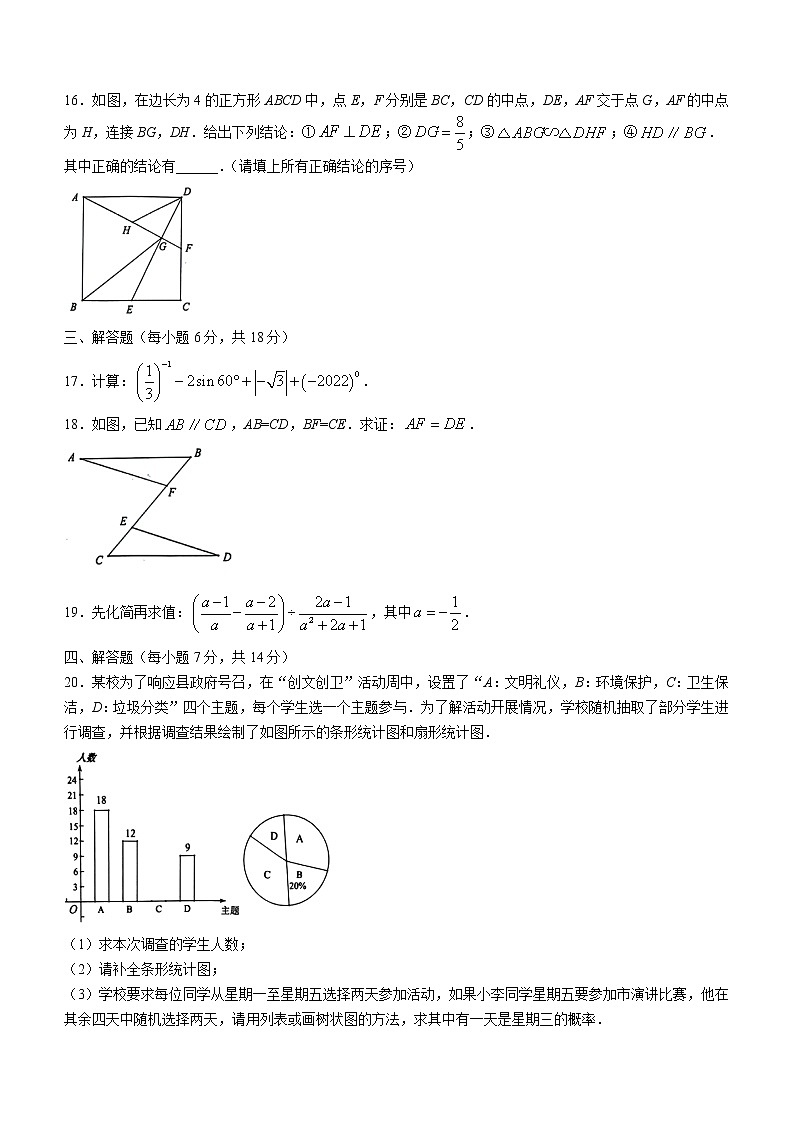
16.如图,在边长为4的正方形ABCD中,点E,F分别是BC,CD的中点,DE,AF交于点G,AF的中点为H,连接BG,DH.给出下列结论:①;②;③;④.
其中正确的结论有______.(请填上所有正确结论的序号)
三、解答题(每小题6分,共18分)
17.计算:.
18.如图,已知,AB=CD,BF=CE.求证:.
19.先化简再求值:,其中.
四、解答题(每小题7分,共14分)
20.某校为了响应县政府号召,在“创文创卫”活动周中,设置了“A:文明礼仪,B:环境保护,C:卫生保洁,D:垃圾分类”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图所示的条形统计图和扇形统计图.
(1)求本次调查的学生人数;
(2)请补全条形统计图;
(3)学校要求每位同学从星期一至星期五选择两天参加活动,如果小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,请用列表或画树状图的方法,求其中有一天是星期三的概率.
21.今年寒假结束后,学生复学,某学校为了增强学生体质,鼓励学生在不聚集的情况下加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,购买的总费用不能超过260元,且要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.
五、解答题(每小题8分,共16分)
22.如图,已知一次函数与反比例函数的图象在第一、三象限分别交于,两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式:
(2)求的面积;
(3)直接写出时x的取值范围.
23.如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东方向,在小区B的西南方向,小区AB之间的距离为米,求供水站M分别到小区A,B的距离.(结果保留根号)
六、解答题(每小题12分,共24分)
24.如图,AD是的直径,AB与相切于点A,直线1与相离,于点B,且OB=5,OB与交于点P,AP的延长线交直线l于点C.
(1)求证:AB=BC;
(2)若的半径为3,求线段AP的长.
25.如图,已知二次函数的图象经过点,与x轴分别交于点A,点.点P是直线BC上方的抛物线上一动点.
(1)求二次函数的表达式;
(2)连接PO,PC,并把沿y轴翻折,得到四边形.若四边形为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
泸县初中2022届第二次学业水平模拟考试
数学试题参考答案
一、选择题(每小题3分,共36分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | C | C | B | A | C | C | D | C | B | D | D |
二、填空题(每小题3分,共12分)
13. 14.3; 15.; 16.①③.
三、解答题(每小题6分,共18分)
17.解:
18.解:
.
当时,
19.证明:证明:
∵,∴,
在和中,
∵,∴;∴.
四、解答题(每小题7分,共14分)
20.解:(1)本次调查的学生人数:(人);
(2)C组的人数为(人),
补全条形统计图如图:
(3)小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,画树状图如图:
或
第1天 第2天 | 星期一 | 星期二 | 星期三 | 星期四 |
星期一 |
| (星期一,星期二) | (星期一,星期三) | (星期一,星期四) |
星期一 | (星期二,星期一) |
| (星期二,星期三) | (星期二,星期四) |
星期三 | (星期三,星期一) | (星期三,星期二) |
| (星期三,星期四) |
星期四 | (星期四,星期一) | (星期四,星期二) | (星期四,星期三) |
|
共有12个等可能的结果,其中有一天是星期三的结果有6个,
其中有一天是星期三的概率为,故答案为.
21.解,(1)设购买一根跳绳需要x元,购买一个毽子需要y元,
依题意,得:,解得:.
答:购买一根跳绳需要6元,购买一个毽子需要4元.
(2)设购买m根跳绳,则购买个毽子,
依题意,得:,
解得:.又∵m为正整数,∴m可以为21,22.
∴共有2种购买方案,方案1:购买21根跳绳,33个毽子.
方案2:购买22根跳绳,32个毽子.
五、解答题(每小题8分,共16分)
22.解:解:(1)把代入中,
解得:m=6,
故反比例函数的解析式为;
把代入,解得,故,
把,代入,得,解得:,
故一次函数解析式为;
(2)如图,设一次函数与x轴交于点C,令y=0,得.∴点C的坐标是,
∴.
故答案为8;
(3)由图象可知,当或时,直线落在双曲线为上方,即,
所以时x的取值范围是或.
23.解:过点M作于N,设米
在中,
∵,,
,,
在中,
∵,
∴,
∴,∴,∴
∴,
故供水站M到小区A的距离是600米,到小区B的距离是米.
六、解答题(每小题12分,共24分)
24.(1)证明:
∵AB与相切,∴,∴,
∵,∴,
∵,∴,∴,∴;
(2)解:连接PD,
∵AD是直径,∴,
∵OB=5,OP=3,∴PB=2,∴,
在中,,
∵,,∴,
∴,即,解得,.
25.解:(1)将点B和点C的坐标代入函数解析式,得
,解得,
二次函数的解析是为;
(2)若四边形为菱形,则点P在线段CO的垂直平分线上,
如图1,连接,则,垂足为E,
∵,∴,∴点P的纵坐标为,当时,,
解得,(不合题意,舍),
∴点P的坐标为;
(3)如图2,
P在直线BC上方的抛物线上,设,,
设直线BC的解析式为,
将点B和点C的坐标代入函数解析式,得,解得.
直线BC的解析为,
设点Q的坐标为,.
当时,,
解得,,,,
,
当时,四边形ABPC的面积最大.
当时,,即P点的坐标为.
当点P的坐标为时,四边形ACPB的最大面积值为.
相关试卷
这是一份四川省泸州市泸县泸县第一中学2022-2023学年八年级下学期期中数学试题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份四川省泸州市泸县泸县第四中学2022-2023学年七年级下学期期中数学试题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年四川省泸州市泸县第一中学中考二模数学试题(含解析),共23页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。








