中考数学 相似三角形复习 精品按照考点整理课件PPT

这是一份中考数学 相似三角形复习 精品按照考点整理课件PPT

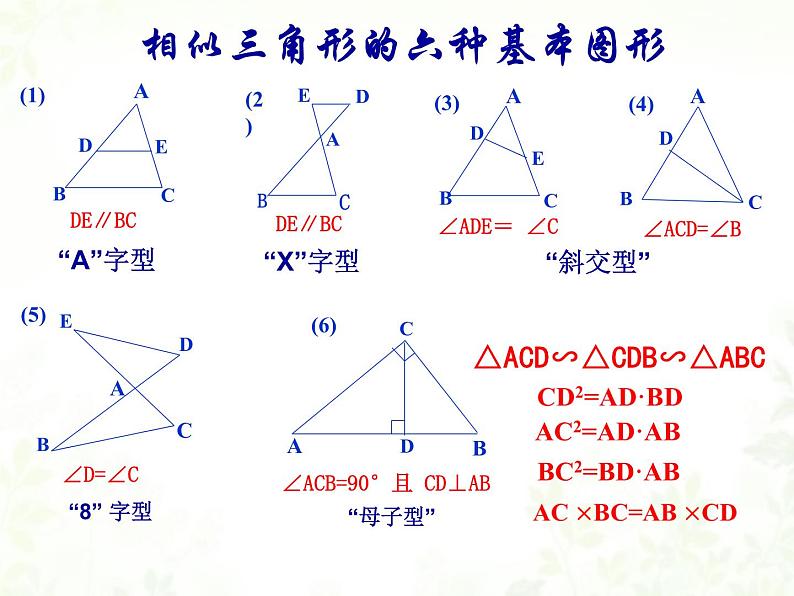
相似三角形复习 对应角相等，对应边成比例的三角形叫做相似三角形。（4）两角对应相等，两三角形相似。（2）三边对应成比例,两三角形相似。（3）两边对应成比例且夹角相等,两三角形相似。相似三角形判定方法（1）平行三角形一边的直线和其他两边(或两边的延长线)相交, 所构成的三角形与原三角形相似.（5）直角三角形中，直角边和斜边对应成比例，两三角形相似。相似三角形的定义 1.对应角相等、对应边成比例。2.对应线段(高、角平分线、中线)的比都等于相似比。3.周长的比等于相似比。4.面积的比等于相似比的平方。 相似三角形的性质相似三角形的六种基本图形∠ADE＝ ∠C“A”字型“X”字型“斜交型”“8” 字型“母子型” AC2=AD·AB BC2=BD·AB △ACD∽△CDB∽△ABC考点1.成比例线段 1.下列各组中的四条线段成比例的是(　　) A．1 cm，2 cm，20 cm，30 cm B．1 cm，2 cm，3 cm，4 cm C．4 cm，2 cm，1 cm，3 cm D．5 cm，0.1m ，10cm，20cm D 10cm, 考点2. 平行线分线段成比例定理 AC=6 2.如图，点E、D分别在△ ABC的边AB、AC上, 若 ED ∥BC,AE=3,BE=6,AD=2, 求线段AC的长. 成比例 成比例 3. 如图，点E、D分别在△ ABC的边AB、AC上, 若 ED ∥BC,AE=3,BE=6,AD=2, 则下列结论中正确的是(　　)A． B．C． D．考点3. 相似形三角形的性质C考点3. 相似形三角形的性质【归纳总结】相似比的平方 相似比 4.如图，点E、D分别在△ ABC的边AB、AC上. 要判断△ ADE与△ ABC相似，需添加一个条件，下列所添条件中错误的是(　　)A．∠AED＝∠C B．ED ∥BCC． D．DC 考点4. 相似三角形的判定两角分别相等的两个三角形相似考点4. 相似三角形的判定相似三角形判定两边对应成比例且夹角相等的两个三角形相似三边对应成比例的两个三角形相似平行于三角形一边的直线与其他两边相交，所构成的三角形与原三角形相似特别地：斜边和一条直角边成比例 的两个直角三角形相似.【归纳总结】 例题1:如图, 在Rt△ABC中，AC=3，BC=4，若P ， Q 分别是 BA ，BC 上的动点，连接 PQ ， BP=CQ=m. 是否存在这样的 m ，使得 △BPQ 与△ABC相似 ?若存在，求出 m 的值；若不存在，请说明理由. 三、典 例 分 析分类讨论∽ △BAC变式:如图,已知A、B是以BD为 直径的⊙O上两点，C为BD上一点，且∠ACB=90 º ，AC=3，BC=4.⊙O是否存在这样的点E，使得△BAE 与△BAC相似.若存在，求AE的长；若不存在，请说明理由.（1）（2）例题2:如图,在矩形ABCD中, 点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF,若设AE= 1 ,AF=2,则△BFG的面积为 .4 解相似三角形基本图形“一线三等角型”的相似三角形（其中∠1=∠2=∠3） 变式1:如图, △ABC、△DEF均为正三角形,点D、E分别在AB,BC上,请找出一个与△ DBE相似的三角形,并给予证明.-2 如图1，在四边形中ABCD，点E、 F分别是AB、 CD的中点，过E点作AB的垂线，过F点作CD的垂线，两垂线交于点G ，连接GA、 GB 、 GC 、 GD 、 EF ，且∠ AGD= ∠ BGC （1）求证： AD=BC.（2）求证：△AGD∽△EGF.图1图1（1）证明：∵GE是AB的垂直平分线，∴GA=GB，同理：GD=GC，在△AGD和△BGC中， GA=GB ∠AGD=∠BGC GD=GC ，∴△AGD≌△BGC（SAS），∴AD=BC；如图1，在四边形中ABCD，点E、 F分别是AB、 CD的中点，过E点作AB的垂线，过F点作CD的垂线，两垂线交于点G ，连接GA、 GB 、 GC 、 GD 、 EF ，且∠ AGD= ∠ BGC （1）求证： AD=BC.（2）求证：△AGD∽△EGF.图1（2）证明：∵∠AGD=∠BGC，∴∠AGB=∠DGC，在△AGB和△DGC中， ，∴△AGB∽△DGC，∴ ，又∵∠AGE=∠DGF，∴∠AGD=∠EGF，∴△AGD∽△EGF；图1（3）如图2，若 AD 、 BC所在直线互相垂直，求 的值.图2（3）解：延长AD交GB于点M，交BC的延长线于点H，如图所示：则AH⊥BH，∵△AGD≌△BGC，∴∠GAD=∠GBC，在△GAM和△HBM中，∠GAD=∠GBC，∠GMA=∠HMB，∴∠AGB=∠AHB=90°，∴∠AGE= ∠AGB=45°，∴ ，又∵△AGD∽△EGF，∴ ．图2M(1)试找出图中的相似三角形?1、如图，四边形CDEF为平行四边形，A为DC上一点，延长EA交FC的延长线于点B 。△ADE ∽ △ACB ∽ △EFB(2)若EA:AB=1:2 ,AC:CD=_____;(3)若△ABC的周长为4,则△BEF的周长为_____.(4)若△ABC的面积为4,则△BEF的面积为_____.2：3692.(安徽中考)如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段 AC的长为( ) 课堂小练笔B（2）点E为BC上任意一点，若∠B= ∠C=∠AEF= 60°, 则△ABE与△ECF的关系还成立吗？说明理由（3）点E为BC上任意一点,若∠B=∠C=∠AEF= α, 则△ABE 与△ECF的关系还成立吗？60°（1）点E为BC上任意一点，若∠B=∠C=∠AEF= 90°, △ABE与△ECF相似吗？说明理由“M”型相似△ABE ∽ △ECF△ABE ∽ △ECF△ABE ∽ △ECF1.矩形ABCD中，把DA沿AF对折，使D与CB边上的点E重合，若AD=10, AB= 8, 求EF的长。 善于在复杂图形中寻找基本型2.如图，在等腰△ABC中，∠BAC=90°，AB=AC=1，点D是BC边上的一个动点(不与B、C重合)，在AC上取一点E，使∠ADE=45°．(1)求证：△ABD∽△DCE；(2)设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出：当BD为何值时，AE取得最小值？相似三角形判定性质1.知识框架3.思想方法周长的比为相似比 对应线段的比为相似比 面积的比为相似比的平方 分类讨论思想对应角相等预备定理两边对应成比例且夹角相等三边对应成比例两角分别相等2.相似三角形基本图形谢谢大家Thank You!厚德外国语学校初中部 罗爱红（3）解：延长AD交GB于点M，交BC的延长线于点H，如图所示：则AH⊥BH，∵△AGD≌△BGC，∴∠GAD=∠GBC，在△GAM和△HBM中，∠GAD=∠GBC，∠GMA=∠HMB，∴∠AGE= ∠AHB=90°，∴∠AGE=∠AGB=45°，∴ ，又∵△AGD∽△EGF，∴ ．图2相似基本图形的运用总结提高1.利用已知相似图形直接求2.学会从复杂图形中分解出基本图形ααα