中考数学复习 反比例函数课件PPT

这是一份中考数学复习 反比例函数课件PPT，共21页。PPT课件主要包含了得m1，双曲线，增大而减小，增大而增大，中心对称，图象性质见下表，知识拓展，数形结合，分类讨论，k2≠0则等内容，欢迎下载使用。

知识点1 反比例函数的概念
反比例函数的三种表达形式：
类型一 反比例函数的概念
21.1. 若函数 是反比例函数，则m2+3m+1= .
知识点2 反比例函数的图像及性质
反比例函数的图象是 .当k＞0时，双曲线的两支分别在第 象限，在每一个象限内，y随x的 ；当k＜0时，双曲线的两支分别在第 象限，在每一个象限内，y随x的 ．双曲线的两支关于坐标原点成 .
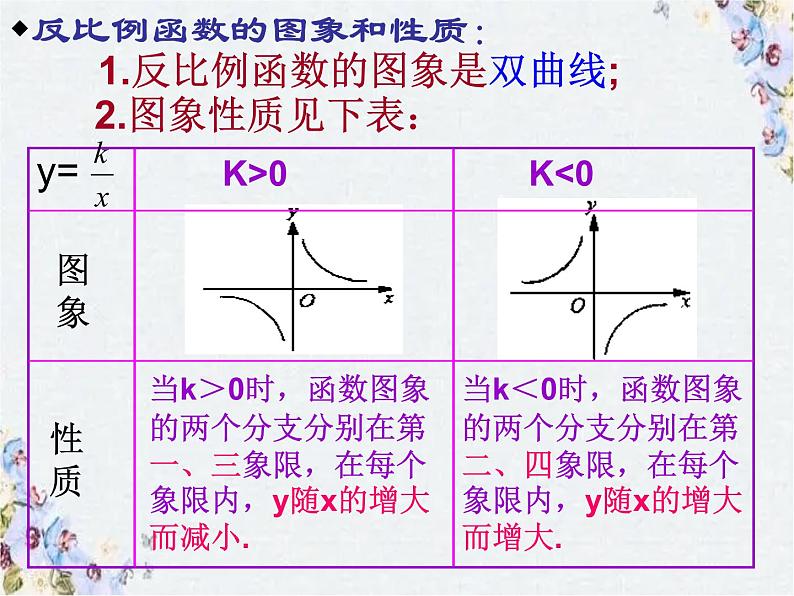
当k＞0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小.
当k＜0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大.
1.反比例函数的图象是双曲线;
反比例函数的图象和性质：
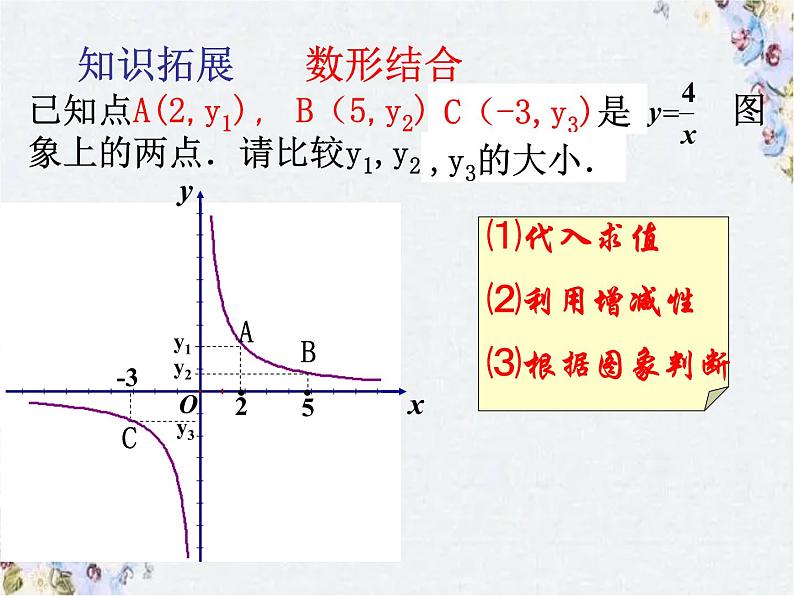
⑴代入求值⑵利用增减性⑶根据图象判断
知识点3:确定反比例函数的关系式
21.3.已知y与x+2成反比例，且当x=2时,y=3，当x=-1时y= 。
21.2.近视眼镜的度数y度与镜片焦距x米成反比例，已知500度近视眼镜片的焦距为0.2米，则眼镜度数y度与镜片焦距x之间的函数关系式是 .
21.11. 已知函数y＝y1＋y2，y1与x成正比例，y2与x成反比例，且当x＝1时，y＝4；当x＝2时，y＝5．（1）求y与x的函数关系式；（2）当x＝－2时，求函数y的值．
思路点拨：本题中，y1与x和y2与x的函数关系中的待定系数不一定相同，故不能都设为k，为了区分，要用不同的字母表示．
解：（1）由题意，设y1＝k1x（k1≠0），
，当x＝1时，y＝4；当x＝2时，y＝5，得
解得k1＝2，k2＝2．
知识点4 反比例函数中比例系数 k的几何意义
反比例函数 中比例系数k的绝对值 的几何意义：如图，过双曲线上任意一点P分别作x轴，y轴的垂线，M、N分别为垂足，则
类型三 利用k的几何意义解题
分析：由k的几何意义可知S1+S阴影=3， S2+S阴影=3 ，而S阴影=1，故 S1+S2=4
21.10.如图，直线y＝mx与双曲线 交于A、B两点，过点A作AM⊥x轴，垂足为M，连结BM,若 =2，则k的值是（ ）A．2 B. －2 C. m D. 4
对称性可知S△AOM=S△BOM=1
22.5.如图，在反比例函数 的图象上，有点P1，P2，P3，P4，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，则S1+S2+S3 = .
知识点5 反比例函数与一次函数综合应用
21.12. 如图，已知A(-4，2)、B(n，-4)是一次函数的图象与反比例函数的图象的两个交点.求此反比例函数和一次函数的解析式；(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
21.14. 如图所示，点A是反比例函数的图象上一点， 轴的正半轴于B点，C是OB的中点；一次函数的图象经过A、C两点，并交y轴于点D(0,-2)，若（1）求反比例函数和一次函数的解析式；（2）观察图象，请指出在y轴的右侧，当 时，x的取值范围．
反比例函数与一次函数综合应用
解：作 轴于E∵∴∴AE=4∵ 为的OB中点，∴∴∴ ∴ A(4,2)将A(4,2)代入 中，得k=8 将A(4,2)和D(0,-2)代入解得：a=1,b=-2 ∴
（2）在y轴的右侧，当 时，