黑龙江省大庆铁人中学2021届高三下学期第三次模拟考试数学（理）试题 Word版含答案

这是一份黑龙江省大庆铁人中学2021届高三下学期第三次模拟考试数学（理）试题 Word版含答案，共14页。试卷主要包含了已知集合，，若，则，已知向量， ，若，则，下列说法等内容，欢迎下载使用。

选择题(本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，
只有一项是符合题目要求的．)
1．已知集合，，若，则（ ）
A．或B．或C．或D．或
2．已知为虚数单位，，若为纯虚数，则（ ）
A．B．C．D．
3．已知向量， ，若，则（ ）
A．B．C．D．
4．已知是两条不重合的直线，是两个不重合的平面，则下列命题中，错误的是( )
A．若，则 B．若，则
C. 若，则 D．若，则或
5.若直线被圆所截弦长最短，则（ ）
A．B．C．D．
6．下列说法：①若线性回归方程为，则当变量x增加一个单位时，y一定增加3个单位；
②将一组数据中的每个数据都加上同一个常数后，方差不会改变；
③线性回归直线方程必过点；
④抽签法属于简单随机抽样，而随机数表法属于系统抽样，
其中错误的说法是（ ）
A．①③B．②③④C．①②④D．①④
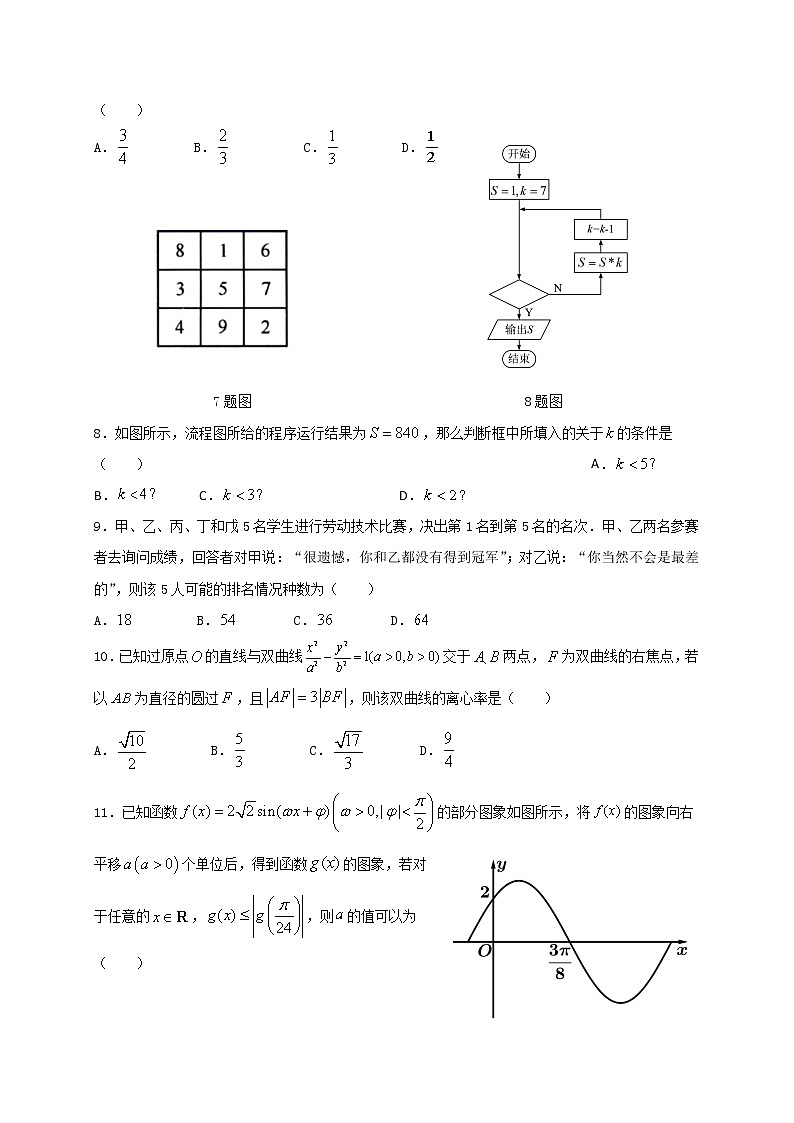
7.“幻方”最早记载于我国公元前500年的春秋时期《大戴礼》中，阶幻方（，）是由前个正整数组成的一个阶方阵，其各行各列及两条对角线所含的n个数之和（简称幻和）相等，例如“3阶幻方”的幻和为15.现从如图所示的3阶幻方中任取3个不同的数，记“取到的3个数和为15”为事件，“取到的3个数可以构成一个等差数列”为事件，则（ ）
A． B． C． D．
7题图 8题图
8．如图所示，流程图所给的程序运行结果为，那么判断框中所填入的关于的条件是（ ） A． B． C． D．
9．甲、乙、丙、丁和戊5名学生进行劳动技术比赛，决出第1名到第5名的名次．甲、乙两名参赛者去询问成绩，回答者对甲说：“很遗憾，你和乙都没有得到冠军”；对乙说：“你当然不会是最差的”，则该5人可能的排名情况种数为（ ）
A． B． C． D．
10．已知过原点的直线与双曲线交于两点，为双曲线的右焦点，若以为直径的圆过，且，则该双曲线的离心率是（ ）
A． B． C． D．
11．已知函数的部分图象如图所示，将的图象向右平移个单位后，得到函数的图象，若对于任意的，，则的值可以为（ ）
A． B． C． D．
12．定义在上的函数若满足：①对任意、，都有；②对任意，都有，则称函数为“中心捺函数”，其中点称为函数的中心.已知函数是以为中心的“中心捺函数”，若满足不等式，当时，的取值范围为（ ）
A．B．C．D．
第II卷（非选择题）
填空题（本大题共4小题，每小题5分，共20分.）
13．若一个空间几何体的三视图如图所示，其中，俯视图为正三角形，则其体积等于______．
14．锐角三角形的面积为，内角的对边分别为，若，则________. 13题图
15．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，其中卷第九勾股中记载：“今有邑，东西七里，南北九里，各中开门．出东门一十五里有木．问出南门几何步而见木?”其算法为：东门南到城角的步数，乘南门东到城角的步数，乘积作被除数，以树距离东门的步数作除数，被除数除以除数得结果，即出南门里见到树，则．若一小城，如图所示，出东门1200步有树，出南门750步能见到此树，则该小城的周长的最小值为（注：1里=300步）________ 里.
16．四面体的四个顶点都在球O上且，，则球O的表面积为 .
三、解答题(共70分，17-21每题12分，22、23选择一题作答，10分，解答应写出文字说明、证明过程或演算步骤．)
17．（12分）已知有限数列共有30项，其中前20项成公差为的等差数列，后11项成公比为的等比数列，记数列的前n项和为．从条件①、条件②、条件③这三个条件中选择一个作为已知，求：
（1）的值；（2）数列中的最大项．
条件①：；
条件②：；
条件③：．
18．（12分）如图，在四棱锥中，底面四边形是正方形，，，点是棱上的点.
（1）证明：平面；
（2）已知，点是上的点，，设二面角的大小为，直线与平面所成的角为，若，求的值.
19．（12分）甲、乙两选手比赛，假设每局比赛甲胜的概率为0.6，乙胜的概率为0.4．甲、乙约定比赛当天上午进行3局热身训练，下午进行正式比赛．
（1）上午的3局热身训练中，求甲恰好胜2局的概率；
（2）下午的正式比赛中：
①若采用“3局2胜制”，求甲所胜局数的分布列与数学期望；
②分别求采用“3局2胜制”与“5局3胜制”时，甲获胜的概率；对甲而言，哪种局制更有利？你对局制长短的设置有何认识？
20．（12分）已知抛物线上一点到焦点的距离是4.
（1）求抛物线的方程；
（2）过点任作直线交抛物线于两点，交直线于点，是的中点，求的值.
21．（12分）已知函数.
（1）求的极值；
（2）证明：.
选做题：请考生在22,、23两题中任选一题作答.注意：只能做所选定的题目，如果多做，则按照所做的第一个题目计分。
22．（10分）在直角坐标系中，曲线：经过伸缩变换后得到曲线，以原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为：．
（1）写出曲线的参数方程和直线的直角坐标方程；
（2）在曲线上求一点，使点到直线的距离最小．
23.（10分）设函数.
（1）解不等式；
（2）若的最小值为，若实数，满足，求证：.
大庆铁人中学2018级高三下学期模拟考试（三）数学（理）答案
一、选择题
填空题
14． 15． 16．
解答题
17．选择条件①：
解：（1）因为的前20项成等差数列，，
所以解得.所以.
因为数列后11项成公比为的等比数列，所以.
综上，.
（2）的前20项成等差数列， .
所以前20项为递增数列. 即：前20项的最大项为.
数列的后11项成等比数列，，所以后11项是递减数列.
即：后11项的最大项为
综上，数列的最大项为第20项，其值为40.
选择条件②：
解：（1）因为的前20项成等差数列，，
所以 所以
因为数列后11项成公比为的等比数列，
，又因为， 所以.
综上，.
（2）的前20项成等差数列， .所以前20项为递减数列.
前20项的最大项为.因为.
i.当时，，
所以当时，.
此时，数列的最大项为第1项，其值为2；
ⅱ.当时，，
后11项的最大项为.
此时，数列的最大项为第21项，其值为18
综上，当时，数列的最大项为第1项，其值为2；
当时，数列的最大项为第21项，其值为18.
选择条件③：
解：（1）因为数列后11项成公比为的等比数列，，
所以，解得. 、所以.
又因为的前20项成等差数列，，
所以.
综上，.
（2）的前20项成等差数列， .所以前20项为递减数列.
前20项的最大项为.
的后11项成等比数列，而，，
，
所以后11项为递增数列.后11项的最大项为
综上，数列的最大项为第30项，其值为10240.
18．（1）因为底面四边形是正方形，所以，
又，，所以平面，
又平面，所以平面平面，
因为，平面，平面平面，
所以平面.
（2）由已知及（1）可知，，，
以为原点，，，的方向分别作为，，轴的正方向建立如图所示的空间直角坐标系.
因为，所以，，，，
，，
得，，，
设平面的法向量为，则由，得
，即，
取，得.
易知平面和平面的一个法向量分别为和.
所以，
，
由，得，
解得.
19．（1）；（2）①分布列见解析；期望为；②“5局3胜制”更有利；比赛局数越多，对水平高的选手越有利．
【详解】
（1）甲恰好胜2局的概率为．
（2）①甲所胜局数x可取0，1，2．
，
，
，
∴甲所胜局数x的分布列为
．
②采用“3局2胜制”时，甲获胜的概率为
，
采用“5局3胜制”时，甲获胜的概率为
．
对甲而言，显然“5局3胜制”更有利，
由此可得出：比赛局数越多，对水平高的选手越有利，
20．（1）；（2）.
【详解】
解：（1）因为①，且点在抛物线上，所以②.
由①②得，所以抛物线的方程为.
（2）由题意知，直线的斜率存在，且不为零，
设点在准线上的投影分别为，，，，，
所以，
∴.
设直线的方程为，代入，得.
设，，则，.
在中，令，得，即.
所以，
即，
所以，
即，∴，
所以.
21．（1）解：的定义域为，
，
在上单调递增，且.
令，得，则的单调递减区间为；
令，得，则的单调递增区间为.
时，取得极小值，极小值为2，无极大值。
（2）证明：设.
令，得；令，得或.
所以当时，取得极大值，且极大值为2，
由（1）知，，故当时，.
设，
，设，
设，易知在上单调递增，
则，则在上单调递增，
从而，则在上单调递增，
则，从而在上单调递增，
所以，故当时，，
从而得证.
22．（1）（为参数）；；（2）点的坐标为．
【详解】
解：（1）由题意，曲线的参数方程为，经过伸缩变换后，曲线的参数方程为，
由得：，
化为直角坐标方程为，
所以，曲线的参数方程为，
直线的直角坐标方程为．
（2）设，
点到直线的距离为，
（其中，，），
当时，即，时，点到直线的距离取到最小值，
此时，，，
，，
所以，点的坐标为．
23．(1) (2)见证明
（1）
当时，，不等式无解
当时，，不等式的解为
综上所述，原不等式的解集为
（2）由（1）易得的最小值为，于是
，

当且仅当，取“”号
1
2
3
4
5
6
7
8
9
10
11
12
B
C
D
A
C
D
D
B
B
A
C
C
x
0
1
2
P
0.16
0.192
0.648