九年级下册6.5 相似三角形的性质评课课件ppt

这是一份九年级下册6.5 相似三角形的性质评课课件ppt，共26页。PPT课件主要包含了学习目标，合作探究，相似三角形的性质，归纳新知等内容，欢迎下载使用。

1.相似三角形的性质.2.相似三角形对应线段的性质.
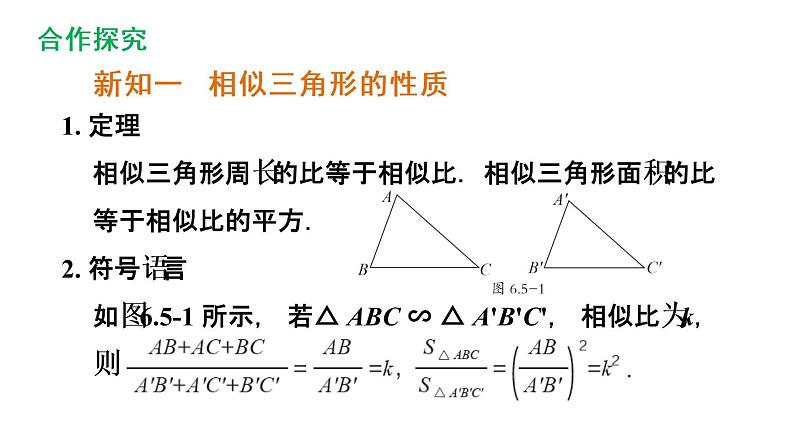
新知一 相似三角形的性质
1. 定理相似三角形周长的比等于相似比．相似三角形面积的比等于相似比的平方．2. 符号语言如图6.5-1 所示， 若△ ABC ∽ △ A'B'C'， 相似比为k， 则
3. 相似多边形的性质定理(1)相似多边形周长的比等于相似比；(2)相似多边形面积的比等于相似比的平方．
特别解读 ：①相似三角形的性质还有对应角相等、对应边成比例；②相似三角形的周长比与面积比不能混淆，相似比等于周长的比，等于面积比的算术平方根．
特别提醒:利用相似三角形周长的比等于相似比时，要注意对应关系，即较大的三角形的周长∶较小的三角形的周长＝ 3 ∶ 2.
如果两个相似三角形的相似比是3 ∶ 2，它们的周长差为8，那么较大的三角形的周长为________ .
解题秘方：紧扣“相似三角形周长的比等于相似比”列方程求解.
解题通法：用方程求解周长的思路：当问题中出现两个相似三角形的周长差求周长时，一般先将两个三角形的周长都用含未知数的代数式表示，再根据“相似三角形周长的比等于相似比”列方程，解方程即可解决问题.
解：设较大的三角形的周长为x，则较小的三角形的周长为x－8.∵这两个相似三角形的相似比为3 ∶ 2，∴这两个相似三角形的周长比为3 ∶ 2，∴ ,解得x=24.
也可设较小的三角形的周长为2x，较大的三角形的周长为3x.∴ 3x-2x=8，∴ x=8，∴较大的三角形的周长为3x=24.
[模拟·宿迁] 如图6.5-2，△ABC ∽△ A′B′C′，BC=6，B′C′=4，AD⊥BC于D，AD=4，求△ A′B′C′ 的面积.
解题秘方：利用“相似三角形面积的比等于相似比的平方”求解.
一题多解:例2 也可以用另一种方法求解，如：过点A′作A′D′⊥B′C′于D′，利用相似三角形的性质先求出△A′B′C′中B′C′边上的高A′D′的长，再利用S△A′B′C′= B′C′·A′ D′求面积.
解：S△ ABC= BC·AD= ×6×4=12.∵△ ABC ∽△ A′B′C′，∴ ，即 ，∴ S△ A′B′C′= ，即△ A′B′C′ 的面积为 .
新知二 相似三角形对应线段的性质
1. 定理 相似三角形对应线段的比等于相似比.2. 符号语言(1)相似三角形对应高的比等于相似比(k). 如图6.5-3 所示，如果△ ABC ∽△ A′B′C′，AD，A′D′ 分别为对应边BC，B′C′ 上的高，则 =k.
(2)相似三角形对应边上中线的比等于相似比(k). 如图6.5-4 所示，如果△ ABC ∽△ A′B′C′，AD，A′D′ 分别为对应边BC，B′C′ 上的中线，则 =k.
(3)相似三角形对应角平分线的比等于相似比(k). 如图6.5-4 所示，如果△ ABC ∽△ A′B′C′，BE，B′E′ 分别为∠ ABC，∠ A′B′C′ 的平分线，则 =k.
特别解读:①相似三角形的“对应线段”一般指三角形的“对应高线” “对应中线” “对应角平分线”，但实际上还包括相似三角形中处在对应位置的所有对应线段，如相似三角形对应边上的中位线等；②书写符号语言时，要找准对应线段，注意符号的顺序性，要写在对应位置，不能颠倒相似三角形中元素的顺序.
[模拟·上海] 如图6.5-5，在△ ABC 中，AD 是BC 边上的高，矩形EFGH 内接于△ ABC，且长边FG 在BC 上，AD 与EH 的交点为P，矩形相邻两边的比为1 ∶ 2. 若BC=30 cm，AD=10 cm，求矩形EFGH的周长.
解题秘方：利用相似三角形对应高的比等于相似比求解.
方法点拨:相似三角形中对应线段的比等于相似比，其中“对应线段”除对应边外，还有对应边上的高、中线，对应角平分线.即：对应线段成比例.
解：设HG=x cm，则EH=2x cm.易得AP⊥EH，PD=HG.∵ AD=10 cm，∴ AP=(10－x)cm.∵四边形EFGH为矩形，∴ EH∥BC.∴∠ AEH= ∠ B, ∠AHE= ∠C.∴△ AEH ∽△ ABC.
∴ (相似三角形对应高的比等于相似比)，即解得x=6.∴ HG=6 cm，EH=12 cm.∴矩形EFGH 的周长为(12+6)×2=36 (cm).
[模拟·南通] 如图6.5-6，D、E 分别是AC、AB 上的点，且∠CDE+ ∠B=180°，F、G 分别是DE、BC 的中点. 若AD=3，AB=5，AG=4，则AF 的值为( )
解题秘方：首先根据相似三角形的判定得出△EAD ∽△CAB，进而得出 ，即可得出答案.
特别警示：利用相似三角形的性质求线段长度的前提是两个三角形必须相似.如果已知条件没有相似，则先证明与已知(或待求)的边有关的三角形相似，然后再运用相似三角形的性质进行计算.
解：∵∠CDE+ ∠ B=180°，∠ADE+ ∠CDE=180°，∴∠ADE=∠B.又∵∠EAD= ∠CAB，∴△ EAD ∽△ CAB，∴ (相似三角形对应中线的比等于相似比)，