苏州吴中、吴江、相城区2020~2021学年初一数学下学期期中学业质量调研试卷（含答案）

2020~2021学年第二学期初一期中学业质量调研试卷

数    学                              2021.4

本试卷由选择题、填空题和解答题三大题组成，共28题，满分130分，考试时间120分钟.

注意事项:

1.答题前，考生务必将自己的学校、班级、姓名、考试号、考场号、座位号，用0.5毫米黑色墨水签字笔填写在答题卷相对应的位置上，并认真核对；

2.答题必须用0.5毫米黑色墨水签字笔写在答题卷指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；

3.考生答题必须答在答题卷上，保持卷面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效.

一、选择题（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填写在答题卷相对应的位置上.）

1.在下列四个图案中，能用平移变换来分析其形成过程的图案是

2.下列运算正确的是

A.   B.   C.     D.

3.下列计算正确的是

A.                   B.

C.           D.

4.下列各组线段不能组成三角形的是

A.4 cm、4 cm、5 cm              B.4 cm、6 cm、10 cm

C.4 cm、5 cm、6 cm              D.5 cm、12 cm、13 cm

5.下列不等式中，是一元一次不等式的是

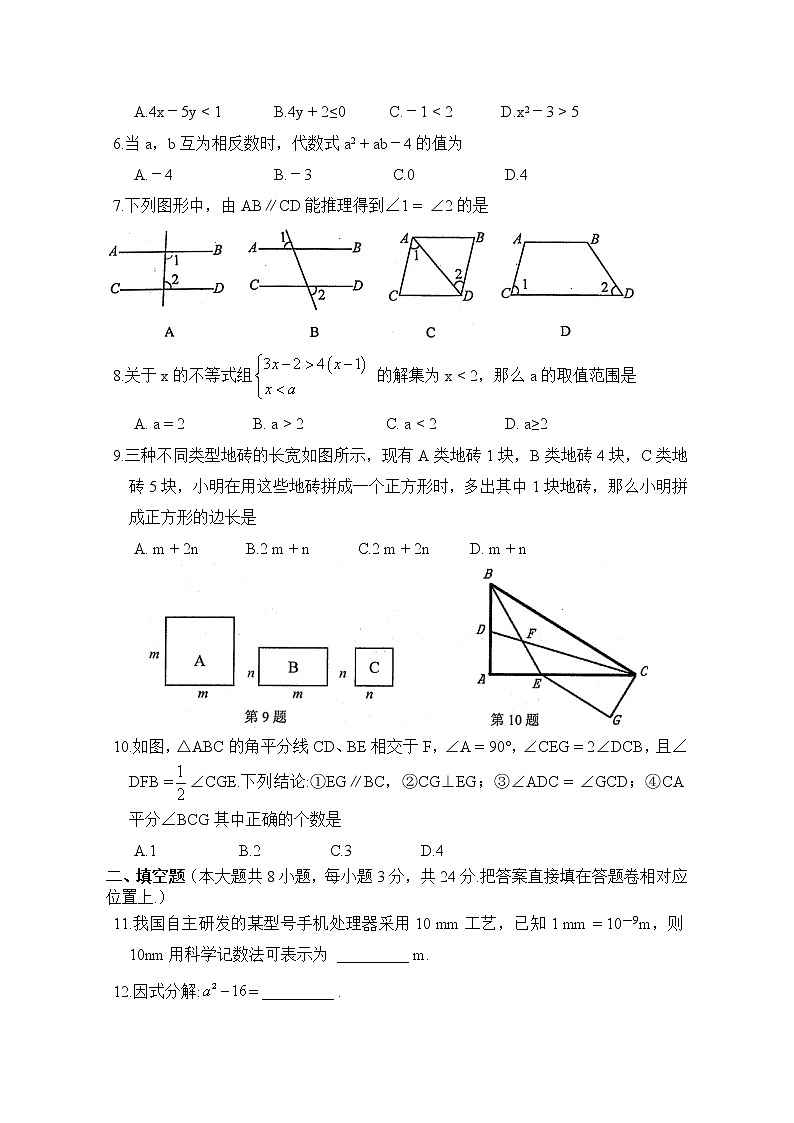
A.4x－5y < 1  B.4y + 2≤0   C.－1 < 2   D.x2－3 > 5

6.当a，b互为相反数时，代数式a2 + ab－4的值为

A.－4          B.－3       C.0       D.4

7.下列图形中，由AB∥CD能推理得到∠1 = ∠2的是

8.关于x的不等式组 的解集为x < 2，那么a的取值范围是 

A. a = 2       B. a > 2      C. a < 2       D. a≥2

9.三种不同类型地砖的长宽如图所示，现有A类地砖1块，B类地砖4块，C类地砖5块，小明在用这些地砖拼成一个正方形时，多出其中1块地砖，那么小明拼成正方形的边长是

A. m + 2n  B.2 m + n  C.2 m + 2n  D. m + n

10.如图，△ABC的角平分线CD、BE相交于F，∠A = 90°，∠CEG = 2∠DCB，且∠DFB =∠CGE.下列结论:①EG∥BC，②CG⊥EG；③∠ADC = ∠GCD；④CA平分∠BCG其中正确的个数是

A.1         B.2      C.3       D.4

二、填空题（本大题共8小题，每小题3分，共24分.把答案直接填在答题卷相对应位置上.）

11.我国自主研发的某型号手机处理器采用10 mm工艺，已知1 mm = 10－9m，则10nm用科学记数法可表示为 _________ m.

12.因式分解:= _________ .

13.关于x的方程2x－2 m = x + 4的解为1，则m的值是_________.

14.若一个多边形的每个外角都是60°，那么这个多边形的边数是_________.

15.若 ，则= _________.

16.如图，将一个宽度相等的纸条按如图方式折叠，如果∠1 = 128°，那么∠2 =  _________.

17.如图，两个正方形边长分别为a、b，如果a + b = 18，ab = 12，则阴影部分的面积为_________.

18.观察下列各式

_________ .

三、解答题（本大题共10小题，共76分.把解答过程写在答题卷相对应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明.）

19.（本题满分16分）计算:

（1） ；         （2） ；

（3） ；  （4） .

20.（本题满分4分）因式分解: .

21.（本图数分5分）解不够式组: ，共求出它的非负整数解。

22.（本题满分5分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示.现将△ABC平移，使点A与点D重合，点E、F分别是B、C的对应点.

（1）请画出平移后的△DEF；

（2）若连接AD、CF，则这两条线段之间的关系是_________；

（3）△ABC的面积是 _________ .

23.（本题满分6分）

先化简，再求值: ，其中 .

24.（本题满分6分）如图，AB∥CD，∠B = 26°，∠D = 39°，求∠BED的度数.完成以下解答过程中的空缺部分:

解:过点E作EF∥AB，

∴∠B = ∠_________（　　　）；

∵∠B = 26°（已知），

∴∠1 =  _________ °（等量代换）；

∵AB∥CD（已知），

∵EF∥AB（作辅助线），

∴EF∥CD；

∴∠D = ∠_________.

∵∠D = 39°（已知），

∴∠2 =  _________ °；

∴∠BED =  _________ ° （等式性质）.

25.（本题满分7分）“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某童装厂准备生产L、M两种型号的童装销往“一带一路”沿线国家和地区.现工厂有甲种布料38米，乙种布料26米.计划用这两种布料生产这两种型号的童装50套进行市场调研.已知做一套L型号的童装需甲种布料0.5米、乙种布料1米，可获利50元；做一套M型号的童装需甲种布料0.9米、乙种布料0.2米，可获利30元.

（1）按要求安排L、M两种型号的童装的生产件数，有哪几种方案?请你设计出来；（2）在你设计的方案中，哪种生产方案获总利润最大?最大利润是多少?

26.（本题满分8分）整式乘法与多项式因式分解是既有联系又有区别的两种变形.

例如， 是单项式乘多项式的法则；把这个法则反过来，得到，这是运用提取公因式法把多项式因式分解.

又如 是多项式的乘法公式；把这些公式反过来，得到，这是运用公式法把多项式因式分解.

把多项式乘多项式法则反过来，将得到什么呢?

事实上，，这样多项式就分解为两个因式与的乘积.

类似地， .

问题一:因式分解

（1） ；  （2） .

问题二:探究

对x、y定义一种新运算F，规定:（其中m，n均为非零常数）.当时，对任意有理数x、y都成立.试探究m，n的数量关系.

27.（本题满分9分）如图，在△ABC中，BC = 6 cm.射线AG∥BC，点E从点A出发沿射线AG以2cm/s的速度运动，当点E出发1s后，点F也从点B出发沿射线BC以3cm/s的速度运动，分别连结AF，CE.设点E运动时间为（s），其中t > 0.

（1）若∠BAF < ∠BAC，则t的取值范围是_________（2）当t为何值时，AE = CF；

（3）是否存在某一时刻t，使S△ABF +S△ACE =S△ABC.

28.（本题满分10分）在△ABC中，∠A = 70°，点D、E分别是边AC、AB上的点（不与A、B、C重合），点P是平面内一动点（P与D、E不在同一直线上），设∠PEB = ∠1，∠DPE = ∠2，∠PDC = ∠3.

（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠2 =  _________ ；（用含有∠1、∠3的代数式表示）

（2）若点P在∠ABC的外部，如图（2）所示，则∠1、∠2、∠3之间有何关系?写出你的结论，并说明理由.

（3）当点P在边CB的延长线上运动时，试画出相应图形，标注有关字母与数字，并写出对应的∠1、∠2、∠3之间的关系式.（不需要证明）