

北师大版初中数学七年级下册期末测试卷(较易)(含答案解析)
展开
北师大版初中数学七年级下册期末测试卷(较易)
考试范围:全册; 考试时间:100分钟;总分120分,
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
- 若,则的值是
A. B. C. D.
- 如图所示,和不是同位角的是
A. B.
C. D.
- 小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离与出发时间之间的对应关系的是
A. B.
C. D.
- 根据下列条件,能作出唯一的的是
A. ,,
B. ,,
C. ,,
D. ,
- 下列说法正确的是
A. 等腰三角形的一个角的平分线是它的对称轴
B. 有一个内角是的三角形是轴对称图形
C. 等腰直角三角形是轴对称图形,它的对称轴是斜边上的中线所在的直线
D. 等腰三角形有三条对称轴
- 如图,飞镖游戏板中的每一块正方形除颜色外都相同,若某人向游戏板投掷飞镖一次假设飞镖在游戏板上,则飞镖落在阴影部分的概率是
A.
B.
C.
D.
- 计算的结果,与下列哪一个式子相同?
A. B. C. D.
- 如图所示,过点画直线的平行线的作法的依据是
A. 两直线平行,同位角相等
B. 同位角相等,两直线平行
C. 两直线平行,内错角相等
D. 内错角相等,两直线平行
- 已知火车站托运行李的费用和托运行李的质量为整数的对应关系如下表所示:
元 |
则与之间的关系式为
A. B.
C. D.
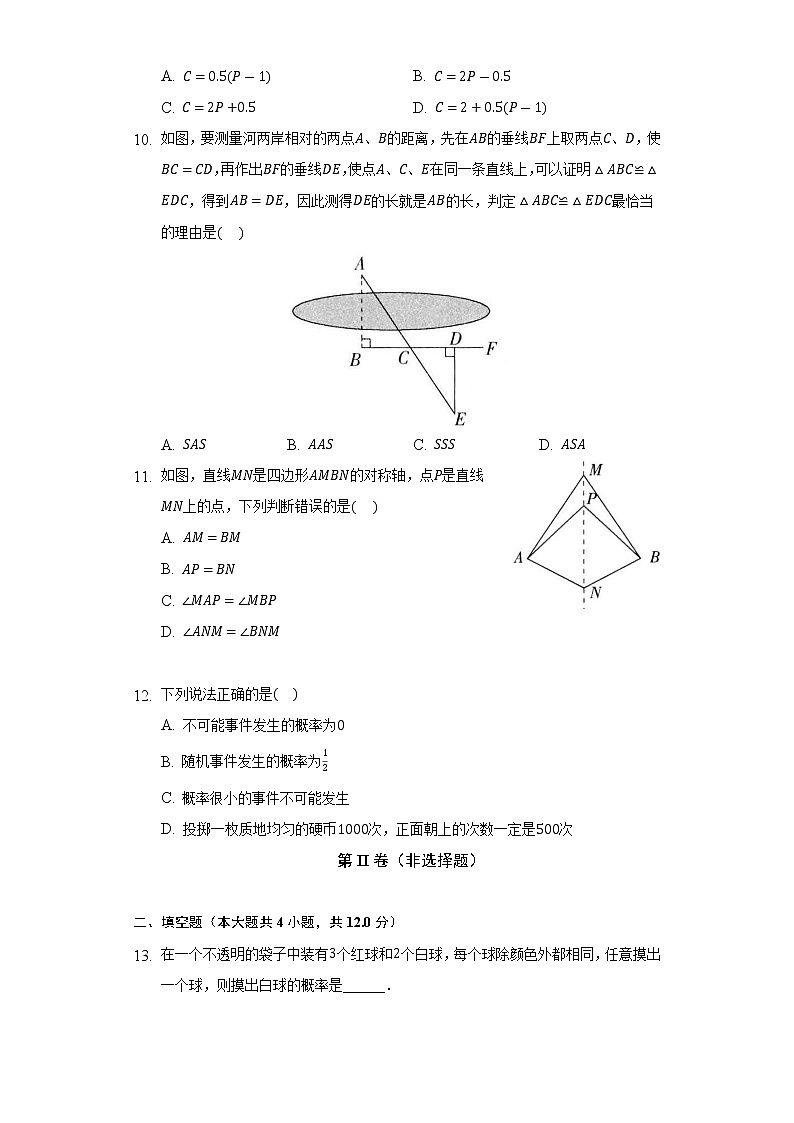
- 如图,要测量河两岸相对的两点、的距离,先在的垂线上取两点、,使,再作出的垂线,使点、、在同一条直线上,可以证明,得到,因此测得的长就是的长,判定最恰当的理由是
A. B. C. D.
- 如图,直线是四边形的对称轴,点是直线上的点,下列判断错误的是
A.
B.
C.
D.
- 下列说法正确的是
A. 不可能事件发生的概率为
B. 随机事件发生的概率为
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币次,正面朝上的次数一定是次
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
- 在一个不透明的袋子中装有个红球和个白球,每个球除颜色外都相同,任意摸出一个球,则摸出白球的概率是______.
- 已知:如图,是的边上的中线,中线则的取值范围是______.
|
- 一个角和它的余角的两倍相等,这个角的补角是______.
- 已知,那么 .
三、解答题(本大题共8小题,共72.0分)
- 先化简,再求值:,其中,.
- 如图,在方格纸中,有两条线段,利用方格纸完成以下操作:
过点作的平行线;
过点作的平行线,与中的平行线交于点;
过点作的垂线,与中的平行线交于点;
用符号表示所作图形中的平行和垂直关系.
- 某市为创建园林城市,在市中心修建了一座半圆形的公园,如图所示小明从圆心出发,沿图中箭头所示的方向在公园的周边散步,匀速完成下列三条线路:线段,半圆弧,线段,正好回到出发点.小明离出发点的距离小明所在位置与点之间线段的长度与时间之间关系的图象如图所示,请根据图象回答下列问题取:
公园的半径是______米,小明的速度是______米分,______;
若沿途小明只遇到了一位同学,并停下来交谈了分钟,且小明在遇到同学的前后始终保持速度不变,求小明遇到同学的地方离出发点的距离;
在的条件下,求小明回到起点的时间.
- 如图,点在上,,,与全等吗?与呢?请说明理由.
- 如图,在平面直角坐标系中,各顶点的坐标分别为:,,,按下列要求作图,保留作图痕迹.
画出关于轴对称的图形点、分布对应、
请在轴上找出一点,满足线段的值最小.
- 如图,有一枚质地均匀的正二十面体形状的骰子,其中的个面标有“”,个面标有“”,个面标有“”,个面标有“”,个面标有“”,其余的面标有“”将这枚骰子掷出后:
数字几朝上的概率最小?
奇数面朝上的概率是多少?
|
- 如图,和交于点,,.
求证:.
|
- 如图,中,,平分,点在上,,,垂足为.
求和的度数.
联结,若,猜想线段的长和的长有什么关系?说明理由.
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查了同底数幂的乘法的运用,关键是熟练掌握同底数幂的乘法法则.
根据同底数幂的乘法法则可得关于的方程,解方程即可.
【解答】
解:,
,
,
解得,
故选A.
2.【答案】
【解析】分析
此题主要考查了同位角的定义,正确把握同位角定义是解题关键.利用同位角的定义,直接分析得出结果即可.
详解
解:和是同位角,故此选项不符合题意;
B.和不是同位角,故此选项符合题意;
C.和是同位角,故此选项不符合题意;
D.和是同位角,故此选项不符合题意.
故选B.
3.【答案】
【解析】
【分析】
本题考查了用图象表示变量之间的关系,根据题意,理清从家出发步行至学校,停留一段时间后乘车返回,明确离开家的距离随时间的变化情况是解题的关键.
从家出发步行至学校时,停留一段时间时,乘车返回时三段分析得到相应的图象,然后即可得解
【解答】
解:从家出发步行至学校时,是一条从原点开始的线段;
停留一段时间时,离家的距离不变,
乘车返回时,离家的距离减小至零,且乘车到家用的时间比步行的时间短,
纵观各选项,只有选项符合.
故选:
4.【答案】
【解析】略
5.【答案】
【解析】
【分析】
本题考查了轴对称图形的知识,解答本题的关键是掌握轴对称及对称轴的定义,根据等腰三角形的三线合一的性质,可得出答案.
【解答】
解:等腰三角形的一个顶角的平分线是它的对称轴,故本选项错误;
B.有一个内角是的等腰三角形是轴对称图形,故本选项错误;
C.等腰直角三角形是轴对称图形,它的对称轴是斜边上的中线所在的直线,故本选项正确;
D.等腰三角形有条对称轴,故本选项错误.
故选C.
6.【答案】
【解析】略
7.【答案】
【解析】解:由多项式乘法运算法则得
.
故选:.
由多项式乘法运算法则:两多项式相乘时,用一个多项式的各项去乘另一个多项式的每一项,再把所得的积相加,合并同类项后所得的式子就是它们的积.
本题考查多项式乘法运算法则,牢记法则,不要漏项是解答本题的关键.
8.【答案】
【解析】
【分析】
本题考查的是平行线的判定定理,即内错角相等,两直线平行,比较简单.在作图的过程中,要求直线、被所截形成的内错角相等,故依据是内错角相等,两直线平行.
【解答】
解:如图所示,根据图中直线、被所截形成的内错角相等,可得依据为内错角相等,两直线平行.
故选D
9.【答案】
【解析】分析
本题考查了用关系式表示的变量间关系,通过表格找出增加,则对应的增加是关键根据表格中的数据可以得到增加,则对应的增加,据此即可求解.
详解
解:根据表可以得到增加,则对应的增加,
则与的对应关系是:.
故选D.
10.【答案】
【解析】在和中,
,故选D.
11.【答案】
【解析】
【分析】
本题考查了轴对称的性质,熟练掌握轴对称的性质是解题的关键.根据直线是四边形的对称轴,得到点与点对应,根据轴对称的性质即可得到结论.
【解答】
解:直线是四边形的对称轴,
点与点对应,
,,,
点时直线上的点,
,
,,D正确,B错误,
故选B.
12.【答案】
【解析】解:不可能事件发生的概率为,故本选项正确;
B.随机事件发生的概率为,故本选项错误;
C.概率很小的事件,不是不发生,而是发生的可能性小,故本选项错误;
D.投掷一枚质地均匀的硬币次,是随机事件,正面朝上的次数不一定是次,故本选项错误.
故选A.
根据不可能事件是指在任何条件下不会发生,随机事件就是可能发生,也可能不发生的事件,发生的可能性大于并且小于,进行判断.
本题考查了不可能事件、随机事件的概念.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
13.【答案】
【解析】解:共有球个,白球有个,
因此摸出的球是白球的概率为:.
故答案为:.
让白球的个数除以球的总数即为摸到白球的概率.
本题考查了概率公式:随机事件的概率事件可能出现的结果数除以所有可能出现的结果数.
14.【答案】
【解析】解:延长至,使,连接.
,,,
≌,
.
在中,,
,
即,
故答案为:.
延长至,使,连接根据证明≌,得,再根据三角形的三边关系即可求解.
此题综合运用了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.
15.【答案】
【解析】解:设这个角是,
根据题意,得,
解得,
这个角是,
这个角的补角是.
故答案为:.
根据互为补角的两个角的和等于,互为余角的两个角的和等于进行计算即可得解.
本题考查了余角与补角,是基础题,熟记概念是解题的关键,要注意求的是这个角的补角不是这个角.
16.【答案】
【解析】略
17.【答案】解:原式
;
当,时,原式.
【解析】本题考查了整式的化简求值;先化简所给的整式,再将,代入求值即可.
18.【答案】解:如图所示:
, ,,.
【解析】本题考查的是平行线和垂线的画法,用字母表示垂直和平行关系等,
所在的横线是满足条件的直线;
过点作的平行线,交中的直线于点,直接作图即可;
过点作的垂线,与中的平行线交于点,则直线即为所求;
根据平行线和垂线的表示方法表示出所作图形中的平行和垂直关系即可.
19.【答案】
【解析】解:由图象可知,花园半径为米,小明速度为米分,半圆弧长为米,则
故答案为:;;;
由已知,第分时小明继续前进,则行进时间为分钟,路程为米,
全程长米,则小明离出发点距离为米;
小明返回起点的时间为分钟.
故在的条件下,求小明回到起点的时间为分钟.
由在变化时,不变可知,半径为米,速度为米分
由根据图象,第分时,小明继续行走,则小明之前行走分,可求出已经行走路北,用全程路程减去已走路程即可;
可求全程时间为用时分钟,再加上停留分钟即可.
本题为动点问题的函数图象探究题,考查了通过函数图象探究图象代表的实际意义,运用数形结合的数学思想.
20.【答案】解:与全等,与全等.
理由如下:
在和中
≌
在和中
≌.
【解析】本题考查了全等三角形的判定:熟练掌握全等三角形的种判定方法,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
21.【答案】解:如图所示:
如图所示:点即为所求.
【解析】直接利用关于轴对称点的性质得出对应点位置进而得出答案;
直接利用轴对称求最短路线的方法得出答案.
此题主要考查了轴对称变换,正确得出对应点位置是解题关键.
22.【答案】解:骰子有个面,个面标有“”,个面标有“”,个面标有“”,个面标有“”,个面标有“”,其余的面标有“”.
,,,
,,,
数字朝上的概率最小;
奇数包括了、、,
.
【解析】先根据概率计算出每个面朝上的概率,从而得出答案;
利用概率公式计算可得.
此题主要考查了概率公式的应用,如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
23.【答案】证明:,
在与中,
,
≌,
,
,
,
,
,
即.
【解析】因为,,,知≌,所以,即,所以有,再根据线段的和差即可得解.
此题考查了全等三角形的判定与性质,利用证明≌是解此题的关键.
24.【答案】解:,平分,
,
,
,
,
,
,;
相等,
理由如下:,
,,
,
,
,
,
,
.
【解析】根据角平分线的的定义得到,根据平行线的性质求出,根据直角三角形的性质求出;
根据梯形的面积公式、三角形的面积公式计算,得出结论.
本题考查的是梯形的面积计算、直角三角形的性质、三角形的面积计算,掌握直角三角形的性质、梯形的面积公式是解题的关键.
湘教版初中数学七年级下册期末测试卷(较易)(含答案解析): 这是一份湘教版初中数学七年级下册期末测试卷(较易)(含答案解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版初中数学七年级下册期末测试卷(较易)(含答案解析): 这是一份北师大版初中数学七年级下册期末测试卷(较易)(含答案解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版初中数学七年级下册期末测试卷(较易)(含答案解析): 这是一份浙教版初中数学七年级下册期末测试卷(较易)(含答案解析),共11页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。












